Physics
 rsg160 (2001-04-15)
rsg160 (2001-04-15)
I have been told that a satellite in a circular orbit that starts
to enter the atmosphere actually speeds up, at first.
When the satellite is outside the atmosphere there are only conservative forces (gravity)
acting and, if the satellite is in a circular orbit, its [speed] is constant.
When it starts to enter the atmosphere there is a small drag force,
since the atmosphere is thin high up.
This force always opposes the motion and I would have guessed that it would slow
the satellite down.
Can you help me in figuring out why the satellite actually speeds up?
-
You're absolutely right.
As long as the drag force remains fairly small, the satellite will gain speed...
The reason for this is simple:
As altitude decreases, speed increases.
A drag force cannot change this unless it's large enough.
The key is that a spacecraft loses altitude at a steady rate during reentry.
It's fairly easy to work this out quantitatively:
Let's call M the mass of the satellite, V its speed and z its altitude.
Let R be the radius of the Earth
(assuming its mass distribution has perfect spherical symmetry)
and let's call g the gravitational field at z = 0.
The kinetic energy of the spacecraft is ½MV 2
and its potential energy is exactly Mgz/(1+z/R)
(normalized to 0 when z = 0; it's about Mgz when z is small).
The sum of these two terms is the total energy E,
which is constant in the absence of drag.
In the presence of a drag force F
(in a direction opposite to that of the velocity),
there's a loss of total energy equal to the power FV of the drag force.
In other words, E' = - FV.
We may use the above expression of E in this,
neglecting the 1/(1+z/R) correction factor for the potential energy
(thus making an error on the order of 1%) and obtain the relation:
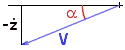
M ( V V' + gz' ) = - FV
Now, we may remark that the quantity (-z' )/ V
is simply sin(a),
the sine of the angle of reentry a
(this is a positive quantity since z is decreasing,
it would be zero for horizontal flight).
Therefore, the above relation translates into:
dV/dt = V' = g sin(a) - F/M
As long as the drag force F is less than
Mg sin(a),
V' is therefore a positive quantity,
which means that the spacecraft will indeed gain speed initially.
For proper re-entry the angle of reentry a
cannot be too small, or else the spacecraft could "bounce" off the atmosphere and be back
into outer space after losing just a little bit of energy.
If no action is taken, an orbiting spacecraft could thus keep bouncing back until
enough energy is lost and/or its reentry angle is sufficiently large
--possibly dangerously so,
since a large a means fast reentry and a lot of heat!
Of course, as the atmosphere becomes denser at lower altitudes,
the drag force F will eventually exceed the above threshold and the spacecraft
will slow down.
 (2002-01-27)
(2002-01-27)
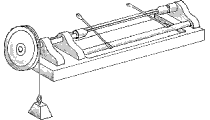
Consider an equilibrium realized, under idealized conditions, when a "perfect"
rope is passed over a frictionless and massless pulley with a ten-pound weight on
one side and a ten-pound monkey on the other [both are initially motionless].
What happens when the monkey decides to climb up the rope?
-
This problem was popularized by Lewis Carroll (1832-1898, né Charles Dodgson),
who agonized over it [recall that the author of Alice in Wonderland was actually a
professor of mathematics at Oxford from 1855 to 1881].
The picture reproduced above once illustrated a discussion of the puzzle by the
mathematical columnist Sam Loyd (1841-1911), who called the problem
"Lewis Carroll's Monkey Puzzle", while stating that it was not known whether
Lewis Carroll originated the question.
(Unfortunately, the solution given by Loyd happens to be erroneous.)
The answer is that the centers of inertia of the weight and the monkey will have
the same vertical motion
(we assume, of course, that the monkey only goes up or down but does not swing the rope).
Thus, if the monkey and the weight are initially motionless at the same height,
they will always face each other no matter what the monkey does.
For example, they will both be in free fall if the monkey lets go of the rope,
and both falls stop when the monkey grabs the rope again.
The reason for this is simply that all the forces that are acting on either the monkey or the
balancing weight are always equal. There are only two such forces for each body, the weight
and the tension of the rope. The weights are equal because the two bodies have the same mass
and the rope also exerts the same force on either body because of the numerous "ideal"
assumptions made here, including the absence of swinging on the monkey's side (so that
the rope exerts only a vertical force in either case).
It's also essential to assume not only the lack of any friction, but also the absence of
mass for both pulley and rope (otherwise the rope's tension would not be the same on
either side of an accelerating pulley and it would vary along the length of an accelerating
rope).
Note also that a "perfect" rope retains its length and transmits instantly its change of
tension. This is clearly unrealistic, but it's logically
consistent with the axioms of classical mechanics.
Changes in tension propagate with infinite speed over the length of a "massless" rope.
Such an assumption would be logically inconsistent in the context of relativistic mechanics.
When the same forces act on bodies of equal masses their speeds change in the same way,
so that the speeds remain equal if they are originally so (and we're told here of an
original equilibrium where both speeds are zero).
Both motions will therefore mirror each other.
From the monkey's perspective, pulling 2 feet of rope will get him only 1 foot higher
from the ground, but will
require as much effort (work) as would be necessary to climb 2 feet on a stationary rope.
That's not surprising in view of the fact that 20 lb were lifted one foot in the
process (the monkey and the weight went up one foot each), which is just as difficult a
task for a 10 lb monkey as lifting his own weight up two feet...
This deceptively simple puzzle has been known to be an excellent way to start a healthy
discussion
about the fundamental principles of classical mechanics.
brentw
(Brent Watts of Hickory, NC.
2001-05-04)
A 24 lb weight, attached to the end of a spring, stretches it 4 inches...
What is the equation of motion if the mass is released from rest
from a point 3 inches above the equilibrium position?
-
Hooke's law states that the force exerted by a spring is proportional to its elongation.
Under standard gravity (g=9.80665 m/s2),
the weight (force) Mg of a mass M of 24 lb (10.88621688 kg)
is 24 lbf (106.757318766 N).
If this corresponds to an elongation of magnitude L=4 inches (0.1016 m),
the force corresponding to an elongation y is therefore -y(Mg/L).
Now, if we decide to count upward elongations positively,
the acceleration y" is therefore such that My"=-Mg-y(Mg/L) (Newton's Law).
If we consider instead the position x=y-L above the equilibrium position,
we have x"+(g/L)x=0 (in the absence of friction or damping).
Introducing the quantity w such that
w2=g/L
(in other words w is
Ö(9.80665/0.1016)
or about 9.82457 rad/s), x is therefore equal to
A cos(wt) +
B sin(wt), for some constants A and B.
Since we are told that, at t=0, x is 3 inches and the speed x' is zero
(the mass is just "released from rest"),
we know that B is zero and A is 3 inches (76.2 mm).
Therefore, the equation of motion is simply
x = A cos(wt),
with A=3"=76.2 mm and
w=9.82456847...rad/s
(corresponding to a period of oscillation T=2p/w
of about 0.64 seconds).
Note that the value of the mass M turns out to be irrelevant here
(the only thing that matters is the magnitude L of the elongation at rest),
but the value of the gravitational field g does matter:
The value of the period of oscillation T
would be different under a gravitational field other than the "standard" one.
 gatman
(Central Florida. 2001-03-31) gatman
(Central Florida. 2001-03-31)
How fast (rpm and mph) are
electrons going around a nucleus?
What factors affect it and how?
-
 For small objects like electrons, quantum mechanics states that
the very notion of trajectory breaks down.
You can't measure both the momentum and the position of a particle:
The product of the uncertainties in the measurements of such conjugate
quantities cannot be less than the so-called Heisenberg limit.
Thus, the electron does not have a precise speed in the classical sense.
However, you can work out what the expected value of the momentum would be
if you were to measure it with infinite precision
(which would mean, then, that you would not know at all where the electron is).
From that momentum, you may derive some kind of expected speed...
For small objects like electrons, quantum mechanics states that
the very notion of trajectory breaks down.
You can't measure both the momentum and the position of a particle:
The product of the uncertainties in the measurements of such conjugate
quantities cannot be less than the so-called Heisenberg limit.
Thus, the electron does not have a precise speed in the classical sense.
However, you can work out what the expected value of the momentum would be
if you were to measure it with infinite precision
(which would mean, then, that you would not know at all where the electron is).
From that momentum, you may derive some kind of expected speed...
This being said (and it had to be said),
you may work out things numerically using something as crude as the
old-fashioned semi-classical Bohr model of the atom
(circular "trajectories" --oh, well-- with an angular momentum which
is only allowed to be n times the
rationalized Planck constant "h-bar"
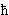 = h/2p).
The number n is the principal quantum number
you may find listed in chemistry books;
it's normally equal to 1 for the electron around an hydrogen nucleus.
= h/2p).
The number n is the principal quantum number
you may find listed in chemistry books;
it's normally equal to 1 for the electron around an hydrogen nucleus.
All told, you'll find that the binding energy of the electron (a negative quantity)
in the Bohr model is
E(n) = -chR/n2,
where c = 299792458 m/s is the speed of light
(Einstein's constant),
h = 6.626 10-34 J.s
is the (unrationalized) Planck constant,
and R=10973731 m-1 is Rydberg's constant.
(I'll neglect the so-called normal mass shift
correcting factor of 1/(1+m/M),
where m/M is the ratio of the mass of the electron to that of the nucleus).
In other words,
E(n) = (-2.18 10-18 J) / n2.
As is the case for planets around the Sun, it turns out that
the kinetic energy ½ mv2 is equal to -E(n).
The mass of the electron is
m = 0.911 10-30 kg.
So, what you get is a speed of the electron which is inversely proportional to n,
namely: v = (2190 km/s) / n.
The largest speed is for n = 1 and corresponds to about 0.73% of the speed of light,
which means it was OK to neglect relativistic effects at our casual level of precision.
If you insist on having the speed expressed in mph,
the formula is v = (4900000 mph)/n.
To obtain the period of rotation around the nucleus,
you need to know the radius of the "orbit"
(again, this is not to be seriously taken as a real trajectory),
which is aon2,
where ao= 0.53 10-10 m
is Bohr's radius.
The period is equal to 2p/v times this,
which means it is proportional to n3:
T = (1.52 10-16 s) n3.
The frequency is thus inversely proportional to the cube of n:
f = (6.58 1015 Hz)/n3,
or if you insist on using rpm's:
f = (395 000 000 000 000 000 rpm)/n3,
since 60 rpm = 1 Hz.
All this pertains to the hydrogen atom (Z = 1).
For a lone electron around a nucleus with Z protons (a so-called hydrogenoid ion),
the energy gets multiplied by Z2 and the speed is therefore multiplied by Z.
Since the size of the "orbit" is divided by Z, the frequency is multiplied by Z2.
To summarize, a lone electron would be expected to go around a nucleus with Z protons
at a speed (Z/n) Vo
and a frequency (Z2/n3 ) fo ,
where :
- Vo is about 0.0073 c, 2190 km/s, 7900 000 km/h,
or 4900 000 mph.
- fo is about 6.58 1015 Hz or 3.95 1017 rpm.
(2002-06-02)
What's the speed of sound in a solid?
-
The waves that propagate in the midst of a solid's bulk are called body waves.
For an homogeneous isotropic material, there are (only) two types of these.
Although both could possibly qualify as "sound",
the term "speed of sound" is best reserved for Vp, the celerity of P-waves
(which are always faster than any other mechanical waves for a given solid).
This is also called longitudinal velocity
(VL = Vp) in contradistinction with the
slower transverse velocity (VT = Vs) of S-waves.
- P waves of speed Vp (primary waves or pressure waves)
are longitudinal compression waves,
for which material moves back and forth along the direction of
propagation.
They're also called push-pull waves.
- S waves of speed Vs (secondary waves or shear waves)
are transverse waves for which material moves side-to-side, in a direction
perpendicular to the direction of propagation.
The "S" may also be remembered as standing for "slow", "shake" or "shock"
(since S-waves often cause the most damage in actual earthquakes because of
amplitudes that are often much larger than P-waves).
At the surface of a solid, different propagation conditions prevail,
corresponding to surface waves
(known to seismologists as Rayleigh waves or Love waves).
In the Lab, it's most convenient to study a given material
in the form of a thin rod.
Two types of waves leave invariant the axis of such a rod:
- Extensional waves have the following speed (Ve):
|
 |
| Ve = Vs |
Ö |
(3Vp 2 -4Vs 2 ) /
(Vp 2 -Vs 2 ) |
They are triggered in a thin rod by some longitudinal stress
(for example, a hammer hitting one end in the direction of the axis).
However, any material with a nonzero Poisson's ratio [that's to say almost any material]
will respond to an axial force [or stress] with both an axial and
a lateral elongation [or strain], which means that the cross section of the rod
varies accordingly and extensional waves thus involve some radial motion.
In materials with a very small Poisson's ratio (like beryllium or cork),
these are virtually identical to P-waves.
- Torsional waves propagate a change in torsion.
They have the same speed (Vs) as shear waves.
Besides the solid's density ( r),
the following dynamic quantities are relevant:
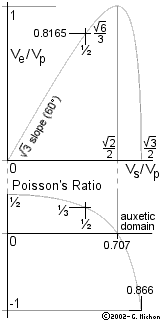
- Poisson's Ratio (n) is the ratio of the lateral
shrinking to the longitudinal elongation which occurs in the direction of a pull.
In a few rare so-called auxetic materials, this may be negative,
which indicates the expansion is both longitudinal and lateral.
- Elasticity (E) is the increase in tension per unit of cross-sectional area
or a small relative increase in the elongation of a wire.
E is often called Young's modulus, in contradistinction
with other elasticity coefficients.
A relative increase in length is a dimensionless quantity called strain,
and E is thus a "stress to strain ratio".
So are the other elasticity coefficients
G, K and l, described below.
All of these are in units of pressure (or stress):
pascals (Pa, N/m2 ) or GPa.
- Rigidity (G), also called
modulus of rigidity, shear modulus, or torsional modulus:
...

- Stiffness
or Bulk modulus (K): The increase in pressure
for a small relative decrease in volume.
K is the reciprocal of compressibility
(ks ).
| K = -V |
æ |
¶p |
ö |
[Subscript "S" is for isentropic,
see below.] |
| è |
 |
ø S |
| ¶V |
- Lamé modulus (l):
l = K-2G/3
is one of the two Lamé constants sometimes used in basic elasticity theory
(the other one is m = G ).
Since l = 3K n / (1+n),
it's negative for auxetic materials
(-1 < n < 0 ).
Dynamic Properties of Selected Isotropic
(or Polycrystalline) Substances
(20°C, 1 atm)
Ranked by
Vp
(speed of sound) |
Vp
(m/s) | Vs
(m/s) | Ve
(m/s) |
n |
E
(GPa) | G
(GPa) | K
(GPa) |
r
(g/L) |
|---|
| Ultrahard Fullerite |
25000 | 9500 | 16000 | 0.42 |
810 | 286 | 1600 |
3170 |
| Diamond |
17450 | 11570 | 17221 | 0.11 |
1043 | 471 | 443 |
3516 |
| Boron |
15000 | 9460 | 14470 | 0.17 |
490 | 210 | 247 |
2340 |
| Beryllium |
12890 | 8820 | 12840 | 0.06 |
306 | 143 | 118 |
1848 |
| Aluminum |
6435 | 3035 | 5000 | 0.36 |
68 | 25 | 79 |
2702 |
| Titanium |
6090 | 3125 | 5080 | 0.32 |
117 | 44 | 109 |
4540 |
| Fused Quartz |
5968 | 3764 | 5757 |
0.17 |
73 | 31 | 37 |
2201 |
| Iron |
5960 | 3240 | 5205 |
0.29 |
213 | 83 | 170 |
7874 |
| Steel (1% C) |
5935 | 3220 | 5175 |
0.29 |
210 | 81 | 168 |
7850 |
| Granite
(LdB) |
5820 | 3360 | 5313 | 0.25 |
75 | 30 | 50 |
2667 |
| Osmium |
5795 | 3135 | 5042 | 0.29 |
574 | 222 | 462 |
22570 |
| Pyrex Glass |
5640 | 3280 | 5175 | 0.24 |
62 | 25 | 41 |
2320 |
| a-Cristobalite |
5415 | 4090 | 5288 |
-0.16 |
65.3 | 39.1 | 16.4 |
2335 |
| Basalt (typ.) |
5140 | 3070 | 4800 | 0.22 |
63 | 25 | 38 |
2740 |
| Crown Glass |
5100 | 2840 | 4536 | 0.28 |
46 | 18 | 34 |
2240 |
| Copper |
4760 | 2324 | 3810 | 0.34 |
130 | 48 | 139 |
8960 |
| Brass 70Cu, 30Zn |
4725 | 2100 | 3485 | 0.38 |
104 | 38 | 141 |
8600 |
| Zinc |
4210 | 2437 | 3850 | 0.25 |
106 | 42 | 70 |
7136 |
| Flint Glass |
3980 | 2380 | 3720 | 0.24 |
54 | 22 | 32 |
3880 |
| Ice (0°C) |
3760 | 2000 | 3228 | 0.30 |
9.6 | 3.7 | 8.1 |
917 |
| Gold |
3240 | 1205 | 2030 | 0.42 |
80 | 28 | 166 |
19330 |
| Nylon 6-6 |
2620 | 1070 | 1790 | 0.40 |
3.6 | 1.3 | 5.9 |
1110 |
| Lead |
2220 | 700 | 1190 | 0.45 |
16 | 6 | 49 |
11350 |
| Rubber |
1550 | 25 | 43 | »0.50 |
0.0018 | 0.0006 | 2.3 |
950 |
| Seawater |
1520 | 0 | 0 | 0.50 |
0 | 0 | 2.4 |
1025 |
| Fresh Water |
1485 | 0 | 0 | 0.50 |
0 | 0 | 2.2 |
998 |
| Mercury |
1450 | 0 | 0 | 0.50 |
0 | 0 | 28.5 |
13546 |
| Cork |
500 | 354 | 500 | »0.00 |
0.062 | 0.031 | 0.021 |
250 |
| Dry Air |
343 | 0 | 0 | 0.50 |
0 | 0 | 142 kPa |
1.204 |
| |
Vp
(m/s) | Vs
(m/s) | Ve
(m/s) |
n |
E
(GPa) | G
(GPa) | K
(GPa) |
r
(g/L) |
|---|
| Ideal Rubber |
V
large | u/Ö3
small |
u
small |
» ½ |
E
small |
E / 3
small |
K
large |
E / u2
K / V2 |
| Fluid |
V | 0 | 0 |
½ |
0 | 0 | K | K / V2 |
| Ideal Cork |
V | V/Ö2 | V |
0 |
E |
E / 2 |
E / 3 |
E / V2 |
| Data compiled from various
sources. May have been adjusted slightly for self-consistency. |
-
The following relations hold between the above quantities
[do multiply by 109 the values tabulated in GPa
for the elasticity coefficients E, G and K]:
9/E = 3/G + 1/K
E = 2(1+n)G
= 3(1-2n)K
= 9 KG / (3K+G)
(Vp)2 = 3K/r (1-n) / (1+n)
=
(K + 4G/3) / r
(Vs)2 = G/r
(Ve)2 = E/r
[Note: Ve > Vs if
n > -½ ]
|
 |
| Ve = Vs |
Ö |
(3Vp 2 -4Vs 2 ) /
(Vp 2 -Vs 2 ) |
x + n = x n + ½
[where x = (Vs/Vp)2 ]
1/x
= 4/3 + K/G = 1 + 3K/E
x = (n-½) / (n-1)
The above elasticity coefficients involved in wave propagation are the
isentropic (or adiabatic) ones.
Static measurements of these coefficients may also be done
fairly slowly under isothermal conditions.
A correction is to be applied to translate such an isothermal coefficient
into an adiabatic one.
For example, the adiabatic bulk modulus
(K = KS) is slightly larger
than its isothermal counterpart
(KT).
At some absolute temperature T, we may call Cp the
specific
heat capacity at constant stress (in J/K per kg)
and a the expansivity
(the relative change in volume per kelvin, also known as
thermal
coefficient of cubical expansion).
If we introduce the quantity
W = r Cp / Ta2
[which is homogeneous to a pressure],
we have:
1/KT =
1/KS + 1/W and:
KS = KT /
(1 - KT / W )
KT = KS /
(1 + KS / W )
| [ a = |
1 |
|
æ |
¶V |
ö |
is 3 times the relative change in length per kelvin
(b) ] |
 |
è |
 |
ø p |
| V |
¶T |
Usually, the quantity W is much larger than K and the relative difference
between the adiabatic and the (smaller) isothermal coefficient
is thus very close to K/W.
For example, in the case of iron, a/3
is listed at 11.8 10-6/K,
whereas Cp is about 448 J/kg K
and r is 7874 g/L.
At 20°C (T = 293.15 K), this makes W
roughly 9600 GPa.
As K itself is about 56 times smaller than that (about 170 Gpa),
we obtain a relative difference of 1.8 %,
which is of borderline relevance here.
For the record, the isothermal and adiabatic versions of rigidity are identical
(G = GS = GT).
On the other hand, the two flavors of Young's modulus obey the same type of relation
we just described above for the bulk modulus, except that the
linear coefficient of expansion (a/3) takes the
place of the cubical one (a) which ends up involving
9W instead of the quantity W defined above, so that we have:
1/ET
= 1/ES + 1/9W.
(You may notice that these relations make the identity
9/E = 3/G + 1/K hold in both the
adiabatic and the isothermal case.)
We are proposing to call the pressure W
the (thermal) wring of the material.
Further Reading, References & Online Data...
- David R. Lide (Editor-in-Chief)
CRC Handbook of Chemistry and Physics
76th Edition (1995-1996)
[page 14-34; data from 1950 to 1960]
- Geophysical Data
for the Geologist
by Kristoffer T. Walker.
About
auxetic materials (negative Poisson's ratio)
- Negative Poisson's Ratio
by Rod Lakes (University of Wisconsin).
- Cristobalite
and Molecular Dynamics (MD)
simulation.
-
Amir Yeganeh-Haeri,
Donald
J. Weidner,
John B. Parise
(1992).
Elasticity of a-cristobalite:
A silicon dioxide with a negative Poisson's ratio.
Science 257: 650-652.
About Utrahard Fullerite :
- V.D. Blank, V.M. Levin, V.M. Prokhorov, S.G. Buga, G.A. Dubitskii,
N.R. Serebryanaya
Elastic properties of ultrahard
fullerites
Journal of Experimental and Theoretical Physics.
October 1998, Volume 87, Issue 4, pp. 741-746.
- V.D. Blank, A.A. Nuzhdin, V.M. Prokhorov, R.Kh. Bagramov
[...] thermodynamic
characteristics of fullerite and various covalent elements
Physics of the Solid State.
July 1998, Volume 40, Issue 7, pp. 1261-1263.
 (2002-06-09)
[ SAW = Surface Acoustic Waves ] (2002-06-09)
[ SAW = Surface Acoustic Waves ]
What's the speed of a Rayleigh wave?
 Rayleigh waves were first described mathematically in 1885 by Lord Rayleigh
(born John William Strutt, 1842-1919) before being
actually observed in earthquakes.
Rayleigh waves were first described mathematically in 1885 by Lord Rayleigh
(born John William Strutt, 1842-1919) before being
actually observed in earthquakes.
A Rayleigh wave is a surface acoustic wave (SAW) which propagates in an
homogeneous and isotropic solid
at the planar boundary with some medium
having little or
no inertia (air or vacuum).
In the midst of such a solid,
body waves propagate with two different celerities;
P-waves travel at the longitudinal celerity Vp and
S-waves travel at the transverse celerity Vs.
We may call x the ratio Vs/Vp
[which is at most ½Ö3 (86.6%)
but only exceeds ½Ö2 (70.7%) in the rare case of
auxetic substances].
This parameter
x is tied to the solid's Poisson's ratio
(n):
n + x2 = n x2 + ½ ;
n = (1-2x2 ) / (2-2x2 ) ;
x2 = (1-2n) / (2-2n)
If we call VR
the celerity of Rayleigh waves, we may call h
the ratio VR/VS
and the following relation holds:
h6 - 8 h4 + 8 (3-2x2 ) h2
- 16 (1-x2 ) = 0
[ VR = h VS ]
As a cubic polynomial of h2,
this equation may have other positive roots with a physical meaning
(see article
by Edouard G. Nesvijski)
but there's only one which is less than unity and
is relevant to pure Rayleigh propagation.
More precisely, h decreases from about
0.95531250 for rubbery materials (x » 0) to
0.87403205 for Ideal Cork (x = ½Ö2) or, possibly, even down to 0.68889218 for the most
auxetic substances we could dream of
(x » ½Ö3).
An approximative formula for ordinary materials
(positive n) was proposed by L. Bergmann (in 1954):
h » (0.87 + 1.12 n) / (1+n)
=
(2.86 - 3.98 x2 ) / (3 - 4 x2 )

 (2002-06-10)
(2002-06-10)
Is there anything harder than diamond?
Two substances are harder than diamond :
- Ultrahard Fullerite (C60 ); positively!
- Carbon Nitride
( b-C3N4 ); probably...
Ultrahard Fullerite
Ultrahard fullerite is a polymerized phase of fullerene discovered in 1995,
which is the object of several patents awarded to Dr. Michael Yu.
Popov.
It is currently used in the
NanoScan (NS)
scanning force microscope (SFM).
Some experimental studies indicate that ultrahard fullerite is about
twice as hard as diamond (approximately 300 GPa, vs. 150 GPa for diamond).
Normally, fullerene crystallizes as a fairly soft yellow solid of low density
(1680 g/L) where buckyballs are held together by
van der Waals forces, similar to what holds together
the hexagonal carbon planes underlying the
structure of graphite (the density of graphite is 2267 g/L).
However, the polymerization of fullerene which occurs at high temperature
under gigapascals of pressure yields an ultrahard phase whose density
(3170 g/L)
compares to that of diamond (3516 g/L).
Under normal conditions, the resulting stable structure
leaves little room for compression...
The material is more than three times stiffer than either diamond or osmium,
according to the above table
(itself based on published acoustic properties of ultrahard fullerite).
From borazon (1957) to carbon nitride and beyond...
In 1989, Marvin Cohen and his graduate student Amy Liu (then at UC Berkeley)
devised a theoretical model to predict a crystal's stiffness
[its bulk modulus], which was thought
until recently
to be a good indicator of the more elusive quality called
hardness.
Noteworthy candidates which did not live up to expectations, according to this model,
included cubic boron nitride. (CBN is the hard form of "BN".
It was first synthesized in 1957 by Dr. Robert H. Wentorf of
the General Electric Company.
It's known in the trade as borazon.)
On the other hand, Cohen's model clearly indicated that a carbon nitride crystal
should be stiffer (and possibly harder) than diamond.
The race was on to obtain the stuff in crystalline form and measure its properties.
Some early efforts
by the team of Yip-Wah Chung (at Northwestern University) resulted in a layered composite of
titanium nitride and carbon nitride (a so-called superlattice)
which was, surprisingly, almost as hard as diamond.
Crystals of carbon nitride were apparently first synthesized at
Lawrence Berkeley Lab (LBL)
by Eugene Haller and William Hansen,
using an approach similar to the synthesis of industrial diamonds.
A 1993 patent for this new superhard material was subsequently awarded to
Cohen, Haller and Hansen.
However, the jury seems still out...
[See March 1998
APS conference, and
May 2000
Nature article.]
Because ultrahard fullerite is so much harder than diamond,
we may venture the guess that it's harder than carbon nitride as well,
but we won't know for sure until someone manages to make a carbon nitride crystal
big enough to test...
Recently
(February 2004)
a new kind of synthetic diamond was found to be
at least 50% harder than natural diamond.
This was obtained at the Carnegie Institutionís
Geophysical Laboratory (Washington, DC)
by submitting to extreme temperatures and pressures (2000°C, 5-7 GPa)
crystals synthesized [much faster than before] by a new chemical vapor deposition (CVD) process.
(2002-06-10)
How is Hardness Defined ?
Hardness
is the resistance to permanent surface damage...
It's totally different from elastic resilience, in spite of a loose correlation.
Unlike stiffness, which is an elastic property of a solid
[quantitatively, stiffness is simply the solid's bulk modulus],
hardness actually indicates the resistance of a solid's surface to
permanent deformation (scratching or indentation) by another solid.
Hardness is somewhat correlated with elastic moduli (the larger the moduli,
the harder the material is expected to be).
This correlation is far from perfect,
as was spectacularly demonstrated in 2002 by a measurement proving
osmium stiffer than diamond, although osmium is not nearly as hard as diamond.
(The term indentability is a less ambiguous alternative for hardness.)
Some news reports have wrongly described osmium as a "soft" metal, whereas
it is one of the hardest metals, with a Mohs hardness of 7...
Hardness does not have a theoretical definition.
Instead, it is evaluated using a number of
practical scales,
which are only roughly compatible with each other.
Hardness values obtained by conversion between such scales are
notoriously fuzzy and/or unreliable.
 | |
The oldest scale of hardness is the Mohs' scale,
which can barely be called quantitative.
It was first devised in 1812 by the German mineralogist Friedrich Mohs (1773-1839)
who published it in 1822.
This scale is based on comparisons with the materials below,
which are assigned the values listed.
If a material scratches another, it's said to be of equal or greater hardness.
Mohs' scale is popular with geologists in the field,
who can use it by carrying a kit containing the standard Mohs minerals and/or other
substances of intermediate hardness:
Lead is 1½,
a fingernail is 2½ (so are galena and gold),
a knife blade is 5½ (so is window glass),
a steel file is 6½,
tungsten is 7½ (tungsten carbide is almost 9).
It's not necessary to have an expensive diamond in such a kit,
except to "identify" other diamonds, because all other minerals
are much softer (as of 2002, only one or two synthetic substances are
known to be harder than diamond, as discussed above).
| MH 1 | MH 2 | MH 3 | MH 4 | MH 5 |
|---|
Talc
Mg3H2(SiO3)4 |
Gypsum
CaSO4 |
Calcite
CaCO3 |
Fluorite
CaF2 |
Apatite
Ca5PO4(OH) |
| Basic Mohs Hardness
(MH) Scale |
|---|
| MH 6 | MH 7 | MH 8 | MH 9 | MH 10 |
|---|
Orthoclase
KAlSi3O8 |
Quartz
SiO2 |
Topaz
Al2SiO4 X2 |
Corundum
Al2O3 | Diamond
C |
Some english speakers have been known to
memorize this sequence using the dubious sentence:
Those Girls Can Flirt And Other Queer Things Can Do.
The rungs in this hardness "ladder" are uneven:
According to some plastometric hardness scales (described below),
diamond (MH 10) is about 3½ times harder than
corundum (MH 9), whereas fluorite or fluorspar
(MH 4; sometimes misspelled "flourite" or "flourspar")
is only 20% harder than calcite (MH 3).
Pure corundum is colorless.
Colored corundum gemstones are called either ruby if red
(because of the presence of chromium) or sapphire otherwise
(mostly blue, in the presence of titanium).
Widely used for grinding and polishing, the emery abrasive contains
» 60% corundum (Al2O3 ),
mixed with magnetite (Fe3O4 )
and spinel (MgAl2O4 ; MH 8)
This problem with Mohs' scale has been somewhat corrected in a so-called
extended scale,
which departs from the above beyond MH 6 and assigns a hardness of 15
to diamond (instead of 10). This extended scale remains much less popular
with geologists than the above original one...
Better quantitative ratings of hardness are mostly obtained with
two very different kinds of instruments,
which may well measure different characteristics of the material under test.
One of these is known as a durometer, the other is called a plastometer
(of various types, named after the specific indenter used).
A durometer ["dur" is French for "hard"] is simply a diamond-pointed
hammer which slides under its own weight in a glass tube and rebounds off the
surface of the material under test.
The height of the rebound is measured and compared with what would be obtained
for some reference material.
If a conventional rating of 100 is assigned to high carbon steel,
this principle defines the so-called Shore scale,
which is divided into overlapping subscales (A, B, C, D, O, OO)
covering progressively softer materials with different measurement specifics.

Other hardness scales are based on the size of the indentation left by a
plastometer after pressing [usually for 30 seconds]
an object (indenter) of known geometry with a calibrated
force against a planar surface of the material under test.
The above picture shows an oblique view of the imprint
obtained on a silicon nitride surface by applying a force of 10 kgf (about 98 N)
to a so-called "Vickers indenter"
(a diamond square pyramid with an angle of 136° between opposing faces).
Such a picture offers clues that the observed remnant is smaller than what
the indentation used to be when the indenter was still in it.
The elastic recovery which took place is properly disregarded in
the evaluation of hardness, which is supposed to be a measure of
how difficult it is to inflict permanent indentations (or scratches)
on the surface of a solid.
A plastometric hardness is then defined (in units of pressure)
as the ratio of the calibrated force to the total surface area of that part of
the indenter at rest which has the same cross-sectional area
as the observed indentation.
In those cases where the indenter is not much harder than the material under test
a theoretical correction may be needed to estimate the size of an indentation
that would have been left by an infinitely hard indenter.
This is also the correct way to extend to diamond
(and/or substances like ultrahard fullerite, the hardest stuff known to Man)
a scale like the Vickers scale, which is normally based on direct readings
from instruments with diamond indenters
(valid for ordinary materials, compared to which diamond may be considered "infinitely hard").
Kelly (Bakersfield, CA. 2001-08-29; e-mail)
I am from Guam, but now live in Bakersfield, California. [...]
I get a sunburn quicker in Guam than in Bakersfield.
I say that it's because being in Guam [latitude 13.5°N] puts me closer
to the Sun than being in Bakersfield [35.4°N].
Am I correct? [...]
-
Not quite so.
What you want to compare is what happens in the two locations
at the same local solar time, say noon.
You may as well compare the
situations of two points B and G on the half meridian directly facing the
Sun (noon local time) and located at the respective latitudes of Bakersfield
and Guam (the longitudes of Bakersfield and Guam are irrelevant).
Let's do a rough calculation first (always a good idea).
The Earth is almost a perfect sphere
of radius R = 6371000 m.
Because the sun is so far away, the difference in the solar distances of two points
 A and B on the Earth is accurately estimated as the distance between the two
parallel planes containing A and B that are perpendicular to the rays from the Sun.
Therefore, you may observe that the difference between the solar distances of
two illuminated points on Earth may not exceed the Earth radius (R).
This overestimate is good enough for our next point...
A and B on the Earth is accurately estimated as the distance between the two
parallel planes containing A and B that are perpendicular to the rays from the Sun.
Therefore, you may observe that the difference between the solar distances of
two illuminated points on Earth may not exceed the Earth radius (R).
This overestimate is good enough for our next point...
The difference in solar distances at noon is thus [much] less
than 6371 km.
Since the Sun is about 150 000 000 km
away, this amounts to less than 0.0000425 of the distance to the Sun.
Now, the energy received from the Sun per unit of area
(physicists call it the radiant illumination)
is inversely proportional to the square of the distance to the Sun.
The difference in radiant illumination
due to the difference in solar distance is thus no more than 0.0085%.
Obviously, such a minuscule difference could not possibly account for
the observation concerning sunburns.
There's another explanation...
What's important is the angle of the Sun's rays, not the distance to the Sun!
This matter of angles also explain why summers are warmer than winters
[in the Northern Hemisphere],
in spite of the fact that the Earth happens to be closer to the
Sun in Winter than in Summer. [Believe it or not.]
The basic reason why it's colder in Winter is that each square mile of the Earth's
surface "sees" the Sun at a more oblique angle and thus receives a narrower
beam of sunlight.
Also, there's less time available between sunrise and sunset to receive the Sun's energy.
Your observation about sunburns, however, involves yet another angular aspect.
Sunburns are directly related to UV exposure in the middle of the day.
It's important to realize that the atmosphere is a natural UV filter.
The lower you see the Sun on the horizon, the thicker the filter.
At noon, the Sun is higher in Guam and will therefore burn you faster.
At sunrise or at sunset, you can't possibly get sunburned.
In Guam or in Bakersfield...
|
 rsg160 (
rsg160 (
 (2002-01-27)
(2002-01-27)








 A and B on the Earth is accurately estimated as the distance between the two
parallel planes containing A and B that are perpendicular to the rays from the Sun.
Therefore, you may observe that the difference between the solar distances of
two illuminated points on Earth may not exceed the Earth radius (R).
This overestimate is good enough for our next point...
A and B on the Earth is accurately estimated as the distance between the two
parallel planes containing A and B that are perpendicular to the rays from the Sun.
Therefore, you may observe that the difference between the solar distances of
two illuminated points on Earth may not exceed the Earth radius (R).
This overestimate is good enough for our next point...