Trigonometry, Elementary & Special Functions
(2002-01-25)
What are some of the common and "special" numerical functions?
-
Well, people have been inventing special functions ad nauseam.
The list is quite literally endless, but we may attempt the beginning of a classification
for those functions which are common enough to have a universally accepted name.
Let's start with the truly elementary functions:
- Polynomial functions:
The value y is obtained from the variable x using only
a finite number of additions and/or multiplications involving given constants.
The simplest such function is the null function (no degree; y = 0),
then [assuming a ¹ 0]
all the other constant functions (degree 0; y = a),
the linear functions (degree 1, very rarely called monic;
y = ax+b),
the quadratic functions (degree 2;
y = ax2+bx+c),
cubic functions,
quartic (or biquadratic), quintic, sextic (rarely hexic),
etc.
Specific adjectives are virtually unused for polynomials beyond degree 6:
degree 7 is either septic
[sic!] or heptic, degree 8 is octic, 9 is nonic, 10 is decic,
and we are told that some have called degree 100 "hectic"...
- Rational functions:
The functions you obtain when division is allowed as well.
A rational function is the quotient of two polynomials. The simplest of these is the
reciprocal function y = 1/x.
- Algebraic functions: The term applies to any function for which the value y and
the variable x are algebraically related, which is to say that there's a two-variable
polynomial P such that P(x,y) = 0.
Only a few of these functions have an explicit name and/or symbol.
The most notable is the
square root function y = Öx.
Like the square root function, most algebraic functions can only be defined continuously
over the complex plane as multivalued functions. Alternately, such functions may
be construed as univalued (ordinary) functions of a variable whose domain is
a so-called Riemann surface for which several points may have the same projection
on the complex plane.
- Elementary transcendental functions:
The simplest of these is y = ex,
the (natural)
exponential function y = exp(x), a function which is equal to its
own derivative (all other such functions are proportional to it).
The exponential function is defined (univalued) over the entire complex plane,
and so are the other transcendental functions which may be defined directly in terms of it,
including the so-called trigonometric or circular functions
(for example y = cos(x) = ½(exp(ix)+exp(-ix))) and the
hyperbolic functions (for example y = ch(x) = ½(exp(x)+exp(-x))).
Modern usage is to consider only the 3 preferred trigonometric functions
(sine, cosine and tangent)
whereas their 3 reciprocals (cosecant, secant and cotangent) are being deprecated.
A similar remark applies to the 3 preferred hyperbolic functions (sh, ch, th), whose
reciprocals are rarely used.
Also classified as elementary transcendental functions are the inverses of
the above, starting with the (natural) logarithm function, y = ln(x),
which is the inverse of the exponential (x = exp(y)).
If continuity is required in the realm of complex numbers,
the logarithm function may only be defined as a multivalued function.
The same thing is true of the inverse trigonometric functions (arcsin, arccos, arctg)
or the inverse hyperbolic functions, which complete the modern list of
elementary functions.
- Important named combinations
of elementary functions.
One example is the Gudermannian or hyperbolic amplitude,
named after the German mathematician
Christoph
Gudermann (1798-1852):
gd(x) =
2 arctg( ex ) - p/2
= 2 arctg( th x/2 )
[NB: gd is odd.]
The derivative of gd(x) is 1/ch(x),
and the inverse of the Gudermannian is a primitive of 1/cos(x)...
In a Mercator conformal map,
the distance to the equator of a point at latitude gd(u) is proportional
to u.
The so-called sine cardinal, or sampling function, is
sinc(x) = sin(x)/x
(it often arises to express the Fourier transtorm of
a rectangular function).
- Gamma function (see below).
Arguably, the most common special function,
or the least "special" of them.
The other transcendental functions listed below are called "special" because
you could conceivably avoid some of them by staying away from many
specialized mathematical topics.
On the other hand, the Gamma function y = G(x)
is certainly most difficult to avoid.
- Elliptic functions and elliptic integrals.
- Exponential and logarithm integral (Ei, li),
sine and cosine integral (si, ci).
- Bessel functions.
- Lambert's W function
(multivalued); if y = W(x), then x = y exp(y).
- Riemann's Zeta function.
A simple function with a complicated structure,
best known for its nontrivial zeroes (its trivial zeroes are the even
negative integers).
Infinitely many of these have been shown (by G.H. Hardy)
to have a real part of ½,
and billions of them have actually been found on that critical line,
but it's still not known whether all of them are there,
as Bernhard Riemann first conjectured in 1859.
The far-reaching implications of this statement, known as the Riemann Hypothesis,
make it the most important unproved mathematical proposition of our times.
- ... ...
As advertised, the list is endless...
(2002-01-29)
What are the basic laws used with trigonometric functions
to obtain all the elements of a triangle when only
some of them are known?
-
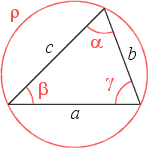A planar triangle is determined by 3 independent quantities.
These could be the 3 sides (a,b,c,
each of which is less than or equal to the sum of the other two),
1 angle and 2 sides, or 1 side and 2 angles.
Instead of a side, you may be given some other length related to the triangle; for example,
the radius r of the circumscribed circle
(see figure at right).
The angular data is usually (but not always) expressed directly in terms of the
inside angle(s) between the sides
(the angles a, b, g, which add up to
p).
| The Law of Sines : |
| 2 r = |
a |
= |
b |
= |
c |
 |
|
|
| sin a |
sin b |
sin g |
|
|---|
| The Law of Cosines : |
c2 = a2 + b2
- 2 ab cos g
|
|---|
| The Law of Tangents : |
| a - b |
= |
tg (a/2 - b/2) |
|
|
| a + b |
tg (a/2 + b/2) |
|
|---|
The Law of Sines may well be the most useful of the three.
It delivers directly any missing quantity in all cases except two,
namely the case where you are given 3 sides
and the case where you are given 2 sides and the angle between them
(the so-called "SAS case", in high-school parlance).
If the 3 sides are given, the Law of Cosines gives you any angle
you may want (via its cosine).
The Law of Cosines will also give you the missing side (c)
when a, b and g are given (the "SAS case").
Having the three sides, you could then obtain either of the missing angles by using
the Law of Cosines again.
However, it's more elegant and more direct to compute
the missing angles with the Law of Tangents
(especially, if you do not care about the value of the missing side c):
Since you know a/2+b/2
(it's equal to p/2-g/2),
the Law of Tangents gives you the (tangent of the) angle
a/2-b/2.
and the missing angles are simply the sum and the
difference of a/2+b/2 and a/2-b/2.
The Law of Tangents was first stated around 1580 by François
Viète (Viette, or Vieta).
It has always been the least popular of the three,
and it's not always found in textbooks...
It may be proved by expressing the ratio
(a - b)/(a + b) in terms of
sin a and sin b,
using the Law of Sines.
The result is then immediately obtained from the following identity for the denominator and
from its counterpart for the numerator
(replace b by -b).
sin a + sin b
= 2
sin(a/2 + b/2) cos(a/2 - b/2)
The Law of Sines itself is proved by remarking that,
if O is the center of the circumscribed circle,
one may consider an isoceles triangle like OAB which has two sides of length
r forming an angle 2g, so that its
base of length c is twice the side opposite to an angle g
in a right triangle of hypotenuse r.
A proof was published in 1342 by the Provençal rabbi
Levi
ben Gerson
(1288-1344; "RaLBaG") who is also known as
Levi ben Gershon, Léon de Bagnols,
Magister Leo Hebraeus, or Gersonides
[son of Gershon
ben Solomon d'Arles].
The Law of Cosines is best proved (or memorized) in the modern context of
vector algebra: Consider two vectors U (from A to C) and V (from A to B),
the vector U-V
goes from B to C and its square (U-V)2 is
|U|2 - 2 U.V + |V|2.
The scalar product ("dot product") U.V is equal to the cosine of the angle
formed by the two vectors multiplied by the product of their magnitudes.
(2003-06-20)
Spherical Trigonometry
What are some basic relations applicable to spherical triangles?
A spherical triangle is a figure on the surface of a sphere of radius R,
featuring three sides which are arcs of great circles
(a "great circle" is the intersection of the sphere with a plane containing the
sphere's center).
Each such figure divides the surface of the sphere into two parts,
whose areas add up to
4pR2 .
Unless otherwise specified, the smaller of these is usually considered the "inside"
of the triangle, but this need not always be so...
The study of spherical triangles is often called spherical trigonometry
and is about as ancient as the simpler planar trigonometry summarized
above.
The internal angles of a spherical triangle always add up to more than a
flat angle (of p radians).
Expressed in radians, the difference
(denoted e, with 0<e <4p)
is usually called the spherical excess, a term coined around 1626
by the French-born Dutch mathematician Albert Girard (1595-1632),
who showed that the surface area of a spherical triangle is
simply equal to:
e R 2 =
( (a + b + g) - p ) R 2
Nevertheless, there are some striking similarities between the two kinds of trigonometries,
including the spherical Law of Sines of Abu'l-Wafa
(940-998):
| sin a |
= |
sin b |
= |
sin c |
|
|
|
| sin a |
sin b |
sin g |
In this, a, b and c are the angular "lengths" of the
sides (as seen from the sphere's center); they are the
curvilinear distances along the
great arcs, using R as a unit.
The spherical excess may also be expressed in terms of these quantities
and the semiperimeter
s = ½ (a+b+c),
using the spherical equivalent of Heron's formula
known as L'Huilier's Theorem:
[tg(e / 4)]2 =
tg[s / 2] tg[(s-a) / 2] tg[(s-b) / 2]
tg[(s-c) / 2]
This beautiful formula is named after the Swiss mathematician
Simon
L'Huilier (1750-1840) who was once a teacher of Charles-François Sturm in Geneva.
(His last name is sometimes also spelled "L'Huillier" or "Lhuilier".)
(V. R. of India.
2000-10-16)
Let cos A + cos B = 2p and sin A + sin B = 2q .
Prove that
tan A/2 + tan B/2 = 2q / (p2 + q2 + p)
-
Let u be tan(A/2) and v be tan(B/2).
We have cos(A) = (1-u2)/(1+u2),
sin(A) = 2u/(1+u2),
and similar relations for B and v. Therefore:
2p = (1-u2)/(1+u2)+(1-v2)/(1+v2)
2q = 2u/(1+u2)+2v/(1+v2)
Expressions such as these, which are symmetrical with respect to u and v, may be expressed
in terms of the sum X=u+v and the product Y=uv.
For example u2+v2 is X2-2Y and
(1+u2)(1+v2) is 1+X2-2Y+Y2 or
X2+(1-Y)2.
The above two relations thus become:
2p(X2+(1-Y)2) = (1-u2)(1+v2)+(1-v2)(1+u2) = 2-2Y2
= 2(1-Y)(1+Y)
2q(X2+(1-Y)2) = (2u)(1+v2)+(2v)(1+u2) = 2X+2XY
= 2X(1+Y)
Adding or subtracting these two after multiplying each either by (1-Y) or X
(and removing the nonzero factor X2+(1-Y)2 which turns up)
greatly simplifies this system of equations, which boils down to a linear system:
pX = q(1-Y) and p(1-Y)+qX = (1+Y)
This may be rewritten
pX+qY = q and qX-(p+1)Y = (1-p).
Solving for X gives X[p(p+1)+q2]=q(p+1)+q(1-p)=2q, which is the desired relation:
tan(A/2)+tan(B/2) = X = 2q/(p2+q2+p)
Also, we may solve for Y and obtain:
tan(A/2)´tan(B/2) = Y = (p2+q2-p)/(p2+q2+p)
brentw (Brent Watts
of Hickory, NC. 2001-03-11)
How do I show that |sin (x + iy)| 2 =
sin 2(x) + sinh 2(y) ?
-
The well-known relation exp(x+iy)=exp(x)(cos(y)+ i sin(y))
may be turned into a definition of the cosine and sine function
(since x and y need not be real in this).
In particular, exp(iz)=cos(z)+ i sin(z),
so sin(z)=(exp(iz)-exp(-iz))/2i. Therefore:
sin(x+iy)
= [eix-y - e-ix+y ] / 2i
= [e-y(cos(x)+ i sin(x)) - expy(cos(x)- i sin(x))]/2i
= [cos(x)(e-y - ey ) + i sin(x)(e-y + ey )] / 2i
So far, we did not assume that x and y were real, now we do:
|z| 2 is the sum of the squares of
the real and imaginary parts of z.
When z is the last of the above expressions, this translates into
|sin(x+iy)|2
= [cos2(x)(e-y - ey )2 + sin2(x)(e-y + ey )2 ] / 4
= [(e-2y + e2y ) - 2 cos(2x) ] / 4
Now, you may identify this expression with the one you give by noticing that:
- sin 2(x) = 1/2 - cos(2x)/2
- sinh 2(y) =
(e 2y + e-2y )/4 - 1/2
Therefore, the entire expression is indeed
sin2(x) + sh2(y),
as advertised.
(J. S. of Canada.
2000-10-15)
How do you solve these equations to exact values for x?
- ln(x-2) - 3 = ln(x+1)
- sin(2x)sin(x) + cos(x) = 0
1) If ln(x-2)-3 = ln(x+1) then ln((x-2)/(x+1)) = ln(e3)
so we must have
(x-2) = (x+1)e3
and x can only be equal to
(2+e3)/(1-e3).
Now, however, this value of x happens to be negative
(it's about -1.157) which makes it unacceptable,
since both (x-2) and (x+1) should be positive
(or else you can't take their logarithm).
Therefore, the original equation does not have any solutions at all!
2) Rewrite sin(2x)sin(x)+cos(x) = 0 as 2 cos(x)sin(x)sin(x) + cos(x) = 0,
or cos(x)[2sin2(x)+1] = 0.
The second factor cannot be zero (it's more than 1)
so this equation boils down to cos(x) = 0,
which has infinitely many solutions of the form
x = (k+½)p,
where k is any integer (positive or not).
| arcsin | arccos | arctan |
|---|
| sin | cos | tan |
|---|
FlyingHellfish (2003-07-28)
In a broken calculator, only the 6 functions shown
at right are available.
Can any positive rational number be obtained from an initial 0?
Yes. Actually, Ö[p/q]
can be obtained for any positive integers p and q, since:
| If p < q, then
Ö[p/q] |
= sin arctan Ö[p/(q-p)]
|
| If p > q, then
Ö[p/q] |
= tan arccos Ö[q/(p+q)]
= tan arccos sin arctan Ö[q/p]
= tan arccos sin arctan sin arctan Ö[q/(p-q)]
|
Using whichever relation is relevant, we may thus reduce any case to a simpler one,
until we reach the trivial case p = q,
which is solved by pushing cos once.
There's (almost) no need to say that the above shows that all positive rationals
can be obtained, since each of them is the square root of its square.
( John of Garland, TX.
2000-11-19)
How are the values of trigonometric functions calculated?
For example, how do we determine that sin(32°) = 0.52991?
-
Basically, the following relation is used:
sin(x) = x
- x3/6
+ x5/120
- x7/5040
+ x9/362880 - ...
+ (-1)k
x2k+1/(2k+1)! + ...
To use this for actual computations,
you've got to remember that x should be expressed in radians
(1° = p/180 rad).
In your example, x = 32 ° = 0.558505360638... rad.
The series "converges" very rapidly:
After 1 term, S = 0.55850536063818
After 2 terms, S = 0.52946976180816
After 3 terms, S = 0.52992261296708
After 4 terms, S = 0.52991924970365
After 5 terms, S = 0.52991926427444
After 6 terms, S = 0.52991926423312
After 7 terms, S = 0.52991926423332
(no change at this precision after this)
Your computer and/or calculator uses this along with a technique called
economization
(the most popular of which is the Chebyshev economization)
which allows a polynomial of high degree (or any reasonable function)
to be very well approximated by a polynomial of lower degree.
In the case of the sine function, the convergence of the above series is so good
that economization only saves you a couple of multiplications for a given precision.
In some other cases (like the atan function), it is quite indispensable.
Footnote: about atan: The atan function has a nice
Chebyshev expansion which allows one to bypass the intermediates
step of a so-called Taylor expansion like the above.
This is rather fortunate because the convergence of atan's
Taylor expansion is quite lousy when x is close to 1.
Modern atan routines use an economized polynomial for x between 0 and 1,
and reduce the computation of atan(x) to that of atan(1/x)
when x is above 1.
See the following article for more details...
What is Chebyshev economization?
Over a finite interval, it is always possible to approximate a continuous function
with arbitrary precision by a polynomial of sufficiently high degree.
In some cases
[one example is the sine function in the previous article]
truncation of the function's Taylor series works well enough.
In other cases, the Taylor series may either converge too slowly or not at all;
the function may not be analytic or, if it is analytic, the radius of
convergence of the Taylor series may be too small to cover comfortably
the desired interval.
If a good polynomial approximation of the continuous real function f(x)
is desired over a finite interval, the following approach may be used and
is in fact the most popular one.
We may consider without loss of generality that the desired interval
is [-1,1] (if it is not, a linear change of variable will make it so),
so that a new variable q can be introduced via the relation
cos q = x.
When the range of q is [0,p],
the range of x is [-1,1] and either variable is a decreasing function of the other.
The fundamental remark is that cos(nq) is a polynomial
function of cos(q).
In fact, either of the following relations defines a polynomial of degree n
known as the Chebyshev polynomial [of the first kind] of degree n.
The symbol "T" is conventionally used for these because
of alternate transliterations from Russian, like Tchebycheff
or Tchebychev.
(the spellings "Chebychev" and "Tchebyshev" also appear).
cos(nq) = Tn(cos q)
or
ch(nq) = Tn(ch q)
[ch = hyperbolic cosine]
The trigonometric formula
cos(n+2)x = 2 cos x cos(n+1)x - cos nx
translates into a simple recurrence relation which makes Chebyshev polynomials
very easy to tabulate: Tn+2(x) =
2x Tn+1(x) - Tn(x)
| T0(x) | = |
1 |
|---|
| T1(x) | = |
| x |
|---|
| T2(x) | = |
-1 | | +2x2 |
|---|
| T3(x) | = |
| -3x | | +4x3 |
|---|
| T4(x) | = |
1 | | -8x2 | | +8x4 |
|---|
| T5(x) | = |
| 5x | | -20x3 | | +16x5 |
|---|
| T6(x) | = |
-1 | | +18x2 | | -48x4 |
| +32x6 |
|---|
| T7(x) | = |
| -7x | | +56x3 | | -112x5 |
| +64x7 |
|---|
| T8(x) | = |
1 | | -32x2 | | +160x4 |
| -256x6 | | +128x8 |
|---|
We'll need to know that, if y2 = x2-1
(y need not be real), then:
Tn(x) = [ (x+y)n + (x-y)n ] / 2
This is a consequence of de Moivre's relation
(with x = cos q
and y = i sin q ):
[ cos q + i sin q ] n
=
exp(i q) n =
exp(i nq) =
cos nq + i sin nq
Now, f(cos q) is obviously an even
function of q (it's continuous because f is).
As such, it has a well-behaved
Fourier expansion which contains only cosines and
translates into the so-called Chebyshev-Fourier expansion of f(x):
| f(cos q) =
co /2 + |
|
cncos(nq)
therefore: f(x) = co /2 +
|
|
cnTn(x) |
The last expression is a series which is always convergent.
For "infinitely smooth" functions, it converges exponentially fast
(as a function of n, the coefficient has to be smaller than the reciprocal of
a polynomial of degree k+1, for any k,
or else the Fourier series of the k-th derivative of
f(cos q) would not converge).
This is much more than what can be said about a Taylor power series...
A truncated Fourier-Chebyshev series is thus expected to give
a much better approximation than a Taylor series truncated at the same order.
What is known as Chebyshev economization is often limited to the
following dubious technique: Take a good polynomial approximant
with many terms (possibly coming from a Taylor expansion) and express it
as a linear combination of Chebyshev polynomials
(whose coefficients may be obtained from the inversion formula below).
This expression may be truncated at some low order to
obtain a good approximation as a polynomial of lower degree.
The following inversion formula is valid in that context, or for a nice
Taylor expansion of the form
f(x) = å an
x n .
[Watch out for the halving of c0 in explicit formulas.]
| cn = 2 |
|
|
ì2p+n
î p |
ü
þ |
a2p+n |
|
| 22p+n |
| x | = |
| T1(x) |
|---|
| 2 x2 | = |
T0(x) | | +T2(x) |
|---|
| 4 x3 | = |
| 3T1(x) | | +T3(x) |
|---|
| 8 x4 | = |
3T0(x) | | +4T2(x) | |
+T4(x) |
|---|
| 16 x5 | = |
| 10T1(x) | | +5T3(x) |
| +T5(x) |
|---|
| 32 x6 | = |
10T0(x) | | +15T2(x) | |
+6T4(x) | | +T6(x) |
|---|
The better approach, whenever possible, is to compute the exact
Chebyshev expansion of the target function and to truncate that
in order to obtain a good approximation by a polynomial of low degree...
For that purpose the above complete inversion formula (infinite sum)
is occasionally handy,
or one may always obtain the coefficients cn via the
Euler formulas, which give:
| cn = |
2 |
ó 1
õ-1 |
f(x) Tn(x) |
dx = |
2 |
óp
õ0 |
f(cos q)
cos(nq) dq |
|
|
|
| p |
 |
p |
| |
| Ö |
1-x2 |
In at least one (important) case, we don't even have to do that, as we may obtain
the Chebyshev expansion directly by algebraic methods...
Consider the arctangent function, which gives the angle in radians between
-p/2 and p/2
whose tangent equals its given [real] argument.
That function is variously abbreviated
Arctg (Int'l/European), arctan (US), atg or atan (computerese).
The following relation is true for small enough arguments.
[It would be true modulo p for unrestricted arguments,
because of the formula giving tg(a+b) as (u+v)/(1-uv) if
u and v are the respective tangents of a and b.]
This may thus be considered an algebraic relation
between formal power series:
Arctg( (u+v)/(1-uv) ) = Arctg(u) + Arctg(v)
With this in mind, we may as well use this formal identity for the complex numbers
u = k [x+iÖ(1-x2
)]
and
v = k [x-iÖ(1-x2 )], so that
2kn Tn(x) =
(u n + v n).
This turns the RHS of the above identity directly into a Chebyshev expansion where the
coefficient cn is simply the coefficient of the arctangent power series
multiplied by 2kn.
On the other hand, the LHS becomes
Arctg(2kx/(1-k2 )).
If we let k be Ö2-1,
this boils down to Arctg(x) and we have:
| Arctg(x) |
=
ån
[2(Ö2-1)2n+1 (-1)n / (2n+1)]
T2n+1(x)
|
| = 2(Ö2-1)
ån
[(2Ö2-3)n / (2n+1)]
T2n+1(x)
|
That's [almost] all there is to it:
We got the Chebyshev expansion at very little cost!
How good is the convergence of this series?
Well, we may first remark that it converges even if the magnitude of
x exceeds unity.
More precisely, when x is larger than 1, Tn(x) is asymptotically
equal to half the n-th power of
x+Ö(x2-1) ,
a quantity which equals the reciprocal of
Ö2-1
when x is Ö2.
Therefore, the series converges if and only if the magnitude of x is
less than (or equal to) Ö2.
More importantly, when the magnitude of x is not more than 1,
a partial sum approximates the whole thing with an error smaller than the coefficient
of the first discarded term.
Suppose we want to use this to find a polynomial approximant of the arctangent function
at a precision of about 13 significant digits
(we need it only over the interval [-1,1], as we may obtain the arctangent of x for x>1
as p/2 minus the arctangent of 1/x).
We find that for 2n+1=31, the relevant coefficient is about
0.88 10-13
so that the corresponding term is just about small enough to be dropped.
The method will thus give the desired precision with an odd polynomial of degree 29,
whose value can be computed using 16 multiplications and 14 additions.
A similar accuracy would require about 10 000 000 000 000
operations with the "straight" Taylor series...
Some economization, indeed!
The above "formal" computation gives the same results as the (unambiguous) relevant
Euler formula for the coefficients of the Chebyshev expansion
of the arctangent function.
This may puzzle a critical reader, since the whole thing seems to work as long as
the quantity 2k/(1-k2 ) is equal to unity,
and this quadratic condition is true not only when k is
Ö2-1, but also for the alternate root
-(Ö2+1) as well.
This latter value, however, leads to a formal Chebyshev series which diverges for
any value of x...
(Mark Barnes, UK.
2000-10-24)
What can you
tell
me about the
Gamma function?
I can work out values for G(x)
if x is integral or x is an integer plus one half.
How can I calculate values for
G(x),
if x is some other value,
like 2.8 or 67/9?
What actually is the function?
The following intimidating definitions of the transcendental Gamma function hide
its simple nature:
G(z+1) is merely the generalization of the factorial function
(z!) to all real or complex values of the number z [besides negative integers].
- Euler integral of the 2nd kind
(valid only if Re(z)>0):
G(z) =
ò0¥e-t tz-1 dt
G(z) =
ò1¥e-t tz-1 dt
+ å (-1)n/(n!(n+z))
-
Gauss' definition:
G(z) =
limn®¥ nzn! / (z(z+1)...(z+n))
-
Weierstrass's definition: (g
being the Euler-Mascheroni constant, namely
0.5772156649015328606065120900824024310421593359399235988...
):
G(z) = e-g z / z
Õ ez/n/(1+z/n)
G(z) has an elementary
expression only when z is either a positive integer n,
or a positive or negative half-integer
(½+n or ½-n):
G(n)
|
|
(n-1)!
G(1/2 + n)
|
|
Öp |
(2n-1)!!
G(1/2 - n)
|
|
(-2)n Öp |
|
|
|
|
|
|
|
2n |
|
(2n-1)!! |
In this, k! ("k factorial") is the product of all positive integers less than or equal to k,
whereas k!! ("k double-factorial")
is the product of all such integers which have the same parity as k, namely
k(k-2)(k-4)...
Note that k!, is undefined (¥) when k is a negative integer
(the G function is undefined at z = 0,-1,-2,-3,...
as it has a simple pole at z = -n with a residue of
(-1)n/n! , for any natural integer n).
However, the double factorial k!! may also
be defined for negative odd values of k:
The expression (-2n-1)!! = -(-1)n / (2n-1)!! ) may be obtained
through the recurrence relation (k-2)!! = k!! / k , starting with k=1.
In particular (-1)!! = 1, so that either of the above
formulas does give G(1/2) = Öp , with n=0.
(You may also notice that either relation holds for positive or negative values of n.)
When the real 2x is not an integer, we do not know any expression of
G(x) in terms of elementary functions:
G(1/3) = 2.67893853470774763365569294097467764412868937795730...
G(1/4) = 3.62560990822190831193068515586767200299516768288006...
G(1/5) = 4.59084371199880305320475827592915200343410999829340...
The real [little known] gem which I have to offer about numerical values of the Gamma
function is the so-called "Lanczos approximation formula" [pronounced
"LAHN-tsosh" and named after the Hungarian mathematician
Cornelius
Lanczos (1893-1974), who published it in 1964].
Its form is quite specific to the Gamma function whose values
it gives with superb precision, even for complex numbers.
The formula is valid as long as Re(z)
[the real part of z] is positive.
The nominal accuracy, as I recall, is stated for
Re(z) > ½,
but it's a simple application of the "reflection formula" (given below)
to obtain the value for the rest of the complex plane with a similar accuracy.
The Lanczos formula makes the Gamma function almost as straightforward to compute
as a sine or a cosine. Here it is:
G(z) =
[1+C1/(z)+C2/(z+1)+ ... +Cn/(z+n-1)
+ e(z)]
´ Ö(2p)
(z+p-1/2)z-1/2
/ ez+p-1/2
e(z) is a small error term whose value is bounded over
the half-plane described above.
The values of the coefficients Ci
depend on the choice of the integers p and n.
For p=5 and n=6, the formula gives a relative error less than
2.2´10-10
with the following choice of coefficients:
C1=76.18009173,
C2= -86.50532033,
C3=24.01409822,
C4= -1.231739516,
C5=0.00120858003,
and C6= -0.00000536382.
I used this particular set of coefficients extensively for years
(other sources may be used for confirmation)
and stated so in my original article here.
This prompted Paul Godfrey
of Intersil Corp. to share a more precise set and his own method to compute any
such sets (without the fear of uncontrolled rounding errors).
Paul has kindly agreed to
let us post his (copyrighted) notes on the subject here.
Some of the fundamental properties of the Gamma function are:
- Reflection formula:
G(z)G(1-z) =
p/sin(pz)
- Recursion formula: G(1+z) =
zG(z)
- Exact values (when n is an integer;
see above when n is negative):
G(n) = (n-1)! and
G(n+1/2) =
Öp (2n)! / (n!4n)
- Multiplication formula (also called "duplication formula" when n=2):
G(nz) =
(2p)(1/2-n/2)
n(nz-1/2) [
G(z) + ... +
G(z+k/n) + ... +
G(z+(n-1)/n) ]
Other interesting remarks about the Gamma function include:
- | G(ix) | 2 =
p / (x sinh px ) for x real
Louis Vlemincq
(Belgium. 2004-02-19; e-mail)
How is the equation t + ln(t) = T ln( I / i ) solved for t and i ?
Taking the exponential of both sides makes it easy to solve for i:
t et = [I / i] T
i = I / ( t e t ) 1/T
To solve for t, you have to use Lambert's W function,
one of the more common "special" functions presented above:
Apply W to both sides of the first of the above equations.
Since, by definition, W(t exp(t)) is equal to t, we obtain:
t = W( [I / i] T )
This solution is valid for positive values of t (the original equation does not make
sense for negative ones). By itself, the equation
x = t exp(t) has 2 real solutions for t when x is
between -1/e and 0 and no real solution when x is less than -1/e.
The radius of convergence of the Taylor series of W is 1/e (0.36787944117...)
W(z)
|
|
|
|
(-n) n-1 |
z n
[ for |z| < 1/e ]
|
|
|
|
n! |
MathWorld
|
Wikipedia
|
Omega constant
On 2004-02-20, Louis Vlemincq
wrote:
Thanks a lot for your kind, quick and learned answer.
It will be most useful to me.
Best regards,
Louis Vlemincq,
Transmission Specialist, BelcomLab.
BELGACOM / 2, rue Carli, 1140 Evere / Belgium
|
|
