|
Calculus
AlisonWonder
(2002-06-23) The Basics:
What is a derivative?
Well, let me give you the traditional approach first.
This will be complemented by an abstract glimpse of the bigger picture,
which is more closely related to the way people actually use
derivatives, once they are familiar with them.
For a given real-valued function f of a real variable,
consider the slope (m) of its graph at some point.
That is to say, some straight line
of equation y = mx+b (for some irrelevant constant b)
is tangent to the graph of f at that point.
In some definite sense, mx+b is the best linear approximation to f(x) when
x is close to the point under consideration...
The tangent line at point x may be defined as the limit of
a secant line intersecting a curve at point x and point x+h,
when h tends to 0.
When the curve is the graph of f, the slope of such a secant is equal to
[ f(x+h)-f(x) ] / h,
and the derivative (m) at point x is therefore the limit of that quantity, as h tends to 0.
The above limit may or may not exist, so the derivative of f at point x may or
may not be defined. We'll skip that discussion.
The popular trivia question concerning the choice of the letter "m"
to denote the slope of a straight line (in most US textbooks) is discussed
elsewhere.
Way beyond this introductory scope, we would remark that
the quantity we called h is of a vectorial nature
(think of a function of several variables),
so the derivative at point x is in fact a tensor
whose components are called partial derivatives.
Also beyond the scope of this article are functions of a complex variable,
in which case the above quantity h is simply a complex number,
and the above division by h remains thus purely numerical (albeit complex).
However, a complex number h (a point on the plane) may approach zero in a variety of ways
that are unknown in the realm of real numbers (points on the line).
This happens to severely restrict the class of functions
for which the above limit exists.
Actually, the only functions of a complex variable which have a derivative
are the so-called analytic functions
[essentially: the convergent sums of power series].
The above is the usual way the concept of derivative is
often introduced.
This traditional presentation may be quite a hurdle to overcome,
when given to someone who may not yet be thoroughly familar with
functions and/or limits.
Having defined the derivative of f at point x,
we define the derivative function
g = f ' = D( f )
of the function f,
as the function g whose value g(x) at point x is the
derivative of f at point x.
We could then prove, one by one, the simple algebraic rules listed
in the first lines of the following table.
These rules are worth committing to memory, as they allows most derivatives to
be easily computed based on the derivatives of just a few elementary functions,
like those tabulated below
(the above theoretical definition is thus rarely used):
u and v are functions of x ;
a, b and n are constants
| |
Function f |
Derivative D( f ) = f ' |
|---|
| Linearity | a u + b v |
a u' + b v' |
Product
Rule | u ´ v |
u' ´ v +
u ´ v' |
| u / v |
[ u' ´ v -
u ´ v' ] / v 2 |
| Chain Rule | u(v) |
v' ´ u'(v) |
| Inversion | v = u-1
| 1 / u'(v) |
|
| Constants | a |
0 |
| Powers | xn |
n x n-1 |
| Logarithms | ln(x) |
1/x = x -1 |
| Exponentials | e x | e x |
| a x | ln(a) a x |
Trigonometric
Functions | sin x | cos x |
| cos x | - sin x |
| tg x | 1 + (tg x)2 |
| ln | cos x | | - tg x |
Hyperbolic
Functions | sh x | ch x |
| ch x | sh x |
| th x | 1 - (th x)2 |
| ln ( ch x ) | th x |
Inverses of
Trigonometric
Functions | arcsin x
(for |x|<1) |
1 / Ö(1-x2 ) |
| arccos x = p/2 - arcsin x | -1 /
Ö(1-x2 ) |
| arctg x | 1 / (1 + x2 ) |
Inverses of
Hyperbolic
Functions | argsh x |
1 / Ö(1+x2 ) |
| argch x
(for |x|>1) | 1 /
Ö(x2 -1) |
| argth x (for |x|<1) | 1 /
(1 - x2 ) |
Hyperbolic
Amplitude
(Gudermannian) | gd x =
2 arctg ex - p/2 | 1 / ch x |
| gd-1 x =
ln tg (x/2 + p/4) | 1 / cos x |
-
One abstract approach to the derivative concept
would be to bypass (at first) the relevance to slopes,
and study the properties of some derivative operator D,
in a linear space of abstract functions
endowed with an internal product (´),
where D is only known to satisfy the following two axioms
(which we may call linearity and product rule,
as in the above table):
| D(au + bv) | = |
a D(u) + b D(v) |
| D( u ´ v ) | = |
D(u) ´ v + u ´ D(v) |
For example, the product rule imposes that D(1) is zero [in the argument of D,
we do not distinguish between
a function and its value at point x, so that "1" denotes the function whose value
is the number 1 at any point x].
The linearity then imposes that D(a) is zero, for any constant a.
Repeated applications of the product rule give the derivative of x raised to the
power of any integer, so we obtain (by linearity) the correct derivative
for any polynomial.
(The two rules may also be used to prove the chain rule for polynomials.)
A function that has a derivative at point x (defined as a limit)
also has arbitrarily close polynomial approximations about x.
We could use this fact to show that both definitions of the D operator coincide,
whenever both are valid
(if we only assume D to be continuous, in a sense which we won't make more precise here).
This abstract approach is mostly for educational purposes at the elementary level.
For theoretical purposes (at the research level)
the abstract viewpoint which has proven to be the most fruitful is totally different:
In the Theory of Distributions,
a pointwise product like the
above (´) is not even defined, whereas everything revolves
around the so-called convolution product
(*), which has the following strange property concerning
the operator D:
D( u * v )
= D(u) * v
= u * D(v)
To differentiate a convolution product (u*v),
differentiate either factor!
 (2002-06-26) (2002-06-26)
What's the "Fundamental Theorem of Calculus" ?
Once known as Barrow's rule, it states that,
if f is the derivative of F, then:
| F(b) -
F(a) = |
ó b
õa |
f (x) dx |
In this, if f and F are real-valued functions of a real variable,
the right-hand side represents the area between the curve
y = f (x) and the x-axis (y = 0),
counting positively what's above the axis and negatively [negative area!] what's below it.
(C. W.. of Grandy, NC.
2000-10-23)
If a car is doing 0 - 60 mph in 4.59 seconds, how far did the car travel?

Well, the most common way to answer this question is to assume that the car
has a constant acceleration, in which case the distance it travels starting at
zero speed is the same distance it would have traveled at a constant velocity
equal to half the final velocity.
Here that's 30 mph times 4.59 s or, with the proper conversion factors:
(30 mi/h) (4.59 s) (h/3600 s) (5280 ft/mi)
= 201.96 ft
= 67.32 yards
Note the foolproof way of converting units, by introducing unity factors
(like 5280 ft/mi) to cancel those units you don't want in the result.
Now, however, any engineer will tell you that acceleration is not constant,
so the above answer is wrong in practice.
It just gives you a rough idea...
 In theory, a rocket vehicle could have a very large acceleration at the very beginning and
almost nothing after a small fraction of a second.
When that's the case the distance would be (almost) twice the above distance.
In theory, a rocket vehicle could have a very large acceleration at the very beginning and
almost nothing after a small fraction of a second.
When that's the case the distance would be (almost) twice the above distance.
 The opposite (silly) case is when you push by hand the above rocket vehicle for more than
4 seconds (moving it only a few feet, a few inches, or nothing at all),
then the rocket fires up and reaches 60 mph in a fraction of a second,
having traveled only a short distance in the process...
The opposite (silly) case is when you push by hand the above rocket vehicle for more than
4 seconds (moving it only a few feet, a few inches, or nothing at all),
then the rocket fires up and reaches 60 mph in a fraction of a second,
having traveled only a short distance in the process...
(2005-02-06)
Integration by parts
A useful technique to reduce the computation of one integral to another.
The product rule states that the derivative
(uv)' of a product of two
functions is u'v+uv'.
When the integral of some function f is sought,
integration by parts is a minor art form which attempts to use this
backwards, by writing f as a product u'v of two functions, one of which
(u') has a known integral (u). In which case:
ò f dx
= ò u'v dx
= uv
- ò uv' dx
This reduces the computation of the integral of f to that of
uv'. The tricky part, of course, is to guess what choice of
u would make the latter simpler...
The choice u' = 1 (i.e.,
u = x and v = f ) is occasionally useful. For example:
ò ln(x) dx
=
x ln(x) - ò (x/x) dx
=
x ln(x) - x
Another classical example pertains to Laplace transforms
( p > 0 )
and/or Heaviside's operational calculus, where all integrals are
understood to be definite integrals
from 0 to +¥
(with a subexponential function
f ):
ò f '(t) exp(-pt) dt
=
- f (0) +
p ò f (t) exp(-pt) dt
rkanchan
(2000-10-17)
What is the perimeter of a parabolic curve,
given the base length and height of [the] parabola?
Choose the coordinate axes so that your parabola has equation y = x2/2p
for some constant parameter p.
The length element ds along the parabola is such that
(ds)2 = (dx)2 + (dy)2, or
ds/dx = Ö(1+(dy/dx)2)
= Ö(1 + x2/p2).
The length L of the arc of parabola from the apex (0,0) to the point
(x,y=x2/2p) is simply the integral of this, namely:
| |
|
 |
|
 |
|
| L | = |
(x/2) |
Ö |
1 + x2/p2 |
+ (p/2) ln( |
Ö |
1 + x2/p2 |
+ x/p ) |
 |
| |
|
 |
|
 |
|
 |
|
| = |
y |
Ö |
1 + p/2y |
+ (p/2) ln( |
Ö |
1 + 2y/p |
+ |
Ö |
2y/p | ) |
For a symmetrical arc extending on both sides of the parabola's axis, the
length is 2L (twice the above). If the "height" is H, and the "base" is B,
the length 2L is obtained from either of the above expressions by plugging in the values
x=B/2, y=H and p=B2/8H. If you want the whole perimeter, including
the length B of the straight base, just add B to the result.
abandonedmule
(2001-04-10)
Find the ratio, over one revolution, of the distance moved by a wheel rolling
on a flat surface to the distance traced out by a point on its circumference.
-
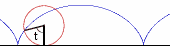
As a wheel of unit radius rolls (on the x-axis),
the trajectory of a point on its circumference is a cycloid,
whose parametric equation is not difficult to establish:
x = t - sin(t)
y = 1 - cos(t)
In this, the parameter t is the abscissa [x-coordinate] of the center of the wheel.
In the first revolution of the wheel (one arch of the cycloid),
t goes from 0 to 2p.
The length of one full arch of a cycloid ("cycloidal arch")
was first worked out in the 17th century by
Evangelista Torricelli (1608-1647), just before the advent of the calculus.
Let's do it again with modern tools:
Calling s the curvilinear abscissa (the length along the curve), we have:
(ds)2 =
(dx)2 + (dy)2 =
[(1-cos(t))2 + (sin(t))2](dt)2
therefore:
(ds/dt)2 = 2 - 2 cos(t) = 4 sin2(t/2)
so, if 0 ≤ t ≤ 2p:
ds/dt = 2 sin(t/2) ≥ 0
The length of the whole arch is the integral of this when t goes
from 0 to 2p
and it is therefore equal to 8,
[since the indefinite integral is -4 cos(t/2)].
On the other hand, the length of the trajectory of the wheel's center
(a straight line) is clearly 2p
(the circumference of the wheel).
In other words, the trajectory of a point on the circumference
is 4/p as long as the trajectory of the center,
for any whole number of revolutions (that's about 27.324% longer, if you prefer).
The ratio you asked for is the reciprocal of that,
namely p/4 (which is about 0.7853981633974...),
the ratio of the circumference of the wheel to the length of the cycloidal arch.
However, the result is best memorized as:
"The length of a cycloidal arch is 4 times the diameter of the wheel."
Pradip Mukhopadhyay
(from Schenectady, NY. 2003-04-07; e-mail)
What is the [indefinite] integral of (tan x)1/3 dx ?
An obvious change of variable is to introduce y = tan x
[ dy = (1+y2 ) dx ],
so the integrand becomes
y1/3 dy / (1+y2 ).
This suggests a better change of variable, namely:
z = y2/3 = (tan x)2/3
[ dz = (2/3)y-1/3 dy ],
which yields z dz = (2/3)y1/3 dy,
and makes the integrand equal to the following rational function of z,
which may be integrated using standard methods
(featuring a decomposition into 3 easy-to-integrate terms):
(3/2) z dz / (1+z3 ) =
¼ (2z-1) dz / (1-z+z2 )
+ (3/4) dz / (1-z+z2 )
- ½ dz / (1+z)
As (1-z+z2 )
is equal to the positive quantity
¼ [(2z - 1)2 + 3] , we obtain:
ò (tan x)1/3 dx
=
¼ ln(1-z+z2 )
+
¼Ö3 arctg((2z-1)/Ö3)
- ½ ln(1+z)
where z stands for | tan x | 2/3
(E. M. of Wisconsin Rapids, WI.
2000-11-21)
[...] Determine the extreme points where the function
z = 3x3+3y3-9xy
is maximized or minimized. Check for second-order-condition.
A necessary (but not sufficient) condition for a smooth function
of two variables to be extremal ("minimized" or "maximized")
is that both its partial derivatives should be zero.
In this case that means 9x2-9y=0 and 9y2-9x=0.
In other words an extremum of z can only occur when (x,y) is either (0,0) or (1,1).
To see whether a local extremum actually occurs,
you must examine the second-order behavior of the
function close to each of the candidate points (in the rare case where the second-order
variations are zero, it's necessary to examine the situation further).
Well, if the second-order partial derivatives are L, M and N, the second-order
variation at point (x+dx,y+dy) is the quantity
½ [ L(dx)2 + 2M(dxdy) + N (dy)2 ]
You may recognize the bracket as a quadratic expression whose sign remains the same
(regardless of the ratio dy/dx) if and only if
its (reduced) discriminant
(M2-LN) is negative.
If it's positive, the point in question is not an extremum.
Back to our example, we have L = 18x, M = -9 and N = 18y.
Therefore, the discriminant is 81(1-4xy).
For the point (0,0) this quantity
is positive (81) so (0,0) is not an extremum.
On the other hand, at the point (1,1)
this quantity is negative (-243) so the point (1,1)
corresponds to the only local extremum of z.
Is this a maximum or a minimum?
Well, just look at the sign of L
(which is always the same as the sign of N for an extremum).
If it's positive, surrounding points yield higher values and, therefore,
you've got a minimum.
If it's negative you've got a maximum.
Here, L = 18, so (1,1) is a minimum.
To summarize: z has only one relative extremum;
it's a minimum of -3, reached at x=1 and y=1.
Does this mean this point is an absolute minimum?
Certainly not!
(When x and y are negative,
a large enough magnitude of either will make z fall below any preset threshold.)
(D. B. of Grand Junction, CO.
2000-10-12)
A particle moves from right to left along the parabola
y = Ö(-x)
in such a way that its x coordinate decreases at the rate of 8 m/s.
When x = -4, how fast is the change in the
angle of inclination of the line joining the particle to the origin?
We assume all distances are in meters.
When the particle is at a negative abscissa x,
the (negative) slope of the line in question is
y/x = Ö(-x)/x and the corresponding
(negative) angle is thus:
a = arctg(Ö(-x)/x)
[In this, "arctg" is the "Arctangent" function, which is also spelled "atan"
in US textbooks.]
Therefore, a varies with x at a (negative) rate:
da/dx = -1/(2´Ö(-x)(1-x)) (rad/m)
If x varies with time as stated, we have dx/dt = -8 m/s, so
the angle a varies with time at a (positive) rate:
da/dt = 4/(Ö(-x)(1-x)) (rad/s)
When x is -4 m, the rate dA/dt is therefore 4/(Ö4
´5) rad/s = 0.4 rad/s.
The angle a,
which is always negative, is thus increasing at a rate of 0.4 rad/s when
the particle is 4 meters to the left of the origin (rad/s = radian per second).
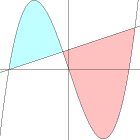
massxv2
(2002-05-18)
What's the area bounded by the following curves?
- y = f(x) = x3 - 9x
- y = g(x) = x + 3
The curves intersect when f(x) = g(x),
which translates into x3 - 10x - 3 = 0.
This cubic equation factors nicely into
(x + 3) (x2 - 3x - 1) = 0 ,
so we're faced with only a quadratic equation...
To find if there's a "trivial" integer which is a root of a polynomial with integer
coefficients [whose leading coefficient is ±1],
observe that such a root would have to divide the constant term.
In the above case, we only had 4 possibilities to try, namely -3, -1, +1, +3.
The abscissas A < B < C of the three intersections are therefore:
A = -3 ,
B = ½ (3 - Ö13)
and
C = ½ (3 + Ö13)
Answering an Ambiguous Question :
The best thing to do for a "figure 8", like the one at hand,
is to compute the (positive) areas of each of the two lobes.
The understanding is that you may add or subtract these,
according to your chosen orientation of the boundary:
- The area of the lobe from A to B (where f(x) is above g(x))
is the integral of f(x)-g(x) = x3 - 10x - 3
[whose primitive is x4/4 - 5x2 - 3x] from A to B,
namely (39Ö13 - 11)/8, or about 16.202...
- The area of the lobe from B to C (where f(x) is below g(x)) is the integral of
g(x)-f(x) from B to C,
namely (39Ö13)/4, or about 35.154...
The area we're after is thus either
the sum (±51.356...) or
the difference (±18.952...) of these two,
depending on an ambiguous boundary orientation...
If you don't switch curves at point B,
the algebraic area may also be obtained
as the integral of g(x)-f(x) from A to C
(up to a change of sign).
(2002-05-18, 2005-08-03)
Signed Planar Areas Consistently Defined
A planar area is best defined as the
apparent area of a 3D loop.
The area surrounded by a closed planar curve may
be defined in general terms, even when the curve does cross itself
many times...
The usual algebraic definition of areas depends on the orientation
(clockwise or counterclockwise)
given to the closed boundary of a simple planar surface.
The area is positive if the boundary runs counterclockwise around the surface,
and negative otherwise
(by convention,
the positive direction of planar angles is always counterclockwise).
In the case of a simple closed curve [without any multiple points]
this is often overlooked, since we normally consider only
whichever orientation of the curve makes the area of its interior positive...
The clear fact that there is such an "interior" bounded by any given closed planar curve
is known as "Jordan's Theorem".
It's a classical example of an "obvious" fact which is rather difficult to prove.
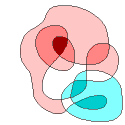
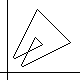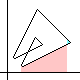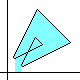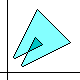
However, when the boundary has multiple points (like the center of a "figure 8"),
there may be more than two oriented boundaries for it,
since we may have a choice at a double point:
Either the boundary crosses itself or it does not (in the latter case,
we make a sharp turn,
unless there's an unusual configuration about the intersection).
Not all sets of such choices lead to a complete tracing of the whole loop.
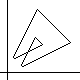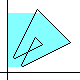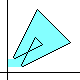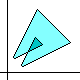
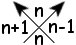 |
|
At left is the easy-to-prove "coloring rule" for a true self-crossing
of the boundary, concerning the number of times the ordinary area
is to be counted in the "algebraic area" dicussed here.
|
It's nice to consider a given oriented closed boundary
as a projection of a three-dimensional loop whose apparent area
is defined as a path integral.
|
S
= ½
òC+
x dy - y dx
=
|
òC+
x dy
=
|
òC+
- y dx
| | |
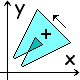 |
 |
 |
 |
brentw (
Brent Watts of Hickory, NC.
2000-11-21)
How do I solve the following differential equations?
- [sin (xy) + xy cos (xy)]dx + [1 + x2 cos (xy)]dy = 0
- [4xy3 - 9y2 +
4xy2]dx + [3x2y2 -6xy +
2x2y]dy = 0
- (3x - y - 5)dx + (x - y + 1)dy = 0
1) For the first DE, what you have is clearly the differential of [x sin(xy) + y]
so the solution is [x sin(xy) + y] = constant.
2) The second DE has a singular solution (the straight line x=0).
The general solution is obtained by noticing that the differential of
[x4y3
- 3x3y2
+ x4y2]
is x2 times the given differential expression.
The solutions to the DE are therefore either curves of equation
[x4y3
- 3x3y2
+ x4y2]
=constant or
"composite" curves made from such algebraic pieces and segments of the singular solution x=0
(joined at the points where they are tangent).
3) The last DE is a no-brainer, but a fairly annoying one.
The general idea is to make a linear change of variables so that the variables "separate"
easily.
For example, you may use x=u+v and y=(u-v)Ö3,
which means
4u=x+yÖ3 and
4y=x-yÖ3.
Your DE then becomes something like (please check):
[2(Ö3+3)v + Ö3-5]du = [2(Ö3-3)u + Ö3+5]dv
If I did manipulate things correctly (please double check),
this means that the solutions are the curves for which the following expression is constant:
[x - yÖ3 + 8/Ö3 - 6]3-Ö3 [x + yÖ3 - 8/Ö3+6]3+Ö3
brentw
(Brent Watts
of Hickory, NC. 2001-04-13/email)
[How do you generalize the method] of variation of parameters when solving
differential equations (DE) of 3rd and higher order? [...]
Will you reply with step-by-step instructions on how to solve
x''' - 3x" + 4x = exp(2t). [...] Thanx.
-
|
This is dedicated to my undergraduate teacher,
who taught me this and much more, many years ago.
|
It's possible to reduce a linear differential equation (DE) of higher order to a system of
first-order linear differential equations involving several variables.
So, let's review this type of system first:
The most general form of a first-order linear system is
dX/dt = AX + B
where X is a column vector of n components (the unknown functions of t),
The square matrix A may depend explicitely on t, whereas B is a column vector
of n explicit functions of t, sometimes called the forcing term(s).
The homogeneous system associated with this is obtained by letting B=0.
Unless A is a constant, finding solutions to the homogeneous system
is an art form in itself, but once you
have n independent such solutions, you may proceed to find a solution to the
forced system by generalizing to n dimensions the common method used with a
single variable (often called the method of "variation of parameter(s)").
Let's do this using only n-dimensional notations:
The fundamental object is the square matrix W formed with the n columns corresponding
to the n independent solutions of the homogeneous system.
Clearly, W itself verifies the homogeneous equation W' = AW.
It's an interesting exercise in the manipulation of
determinants to prove that det(W)' = tr(A) det(W)
(HINT: Differentiating just the i-th line of W gives a matrix
whose determinant is det(W) multiplied by the i-th component
in the diagonal of the matrix A).
Since det(W), the so-called "Wronskian", is
solution of a such a first-order linear DE, it is proportional to the exponential of
some function and is therefore either nonzero everywhere or zero everywhere.
Also, you may want to notice that the two Wronskians obtained for different sets of
solutions of the homogeneous equation are functions of t that are proportional to
each other!
Homogeneous solutions that are linearly independent at some point are therefore
independent everywhere and W(t) has an inverse for any t.
Without loss of generality, we may thus look for the solution X to the nonhomogeneous
system in the form X = WY. We obtain:
AX + B = X' = W'Y + WY' =
AWY + WY'
= AX + WY'
Therefore B = WY'
Y is thus simply obtained by integrating W-1 B.
All told, the general solution of the nonhomogeneous system may be expressed as follows,
with a constant vector K whose n components are
the n expected "constants of integration".
This looks very much like the corresponding formula for a single variable (except that
X, W, K and B are not scalars):
|
X(t) = W(t) [ K +
ò t
W-1(u) B(u) du ]
|
Now, a linear differential equation of order n has the following form
(where ak and b are explicit functions of t):
x(n) +
an-1 x(n-1) + ... +
a3 x(3) + a2 x" + a1 x' + a0 x
= b
This reduces to the above first-order system, if we introduce a vector X whose
components are the successive derivatives of x.
We have X' = AX + B with the following notations:
| A = |
 |
 |
|
 |
 |
X = |
 |
 |
|
 |
 |
B = |
 |
 |
|
 |
 |
|
0 |
1 |
0 |
0 |
... |
0 |
0 |
|
|
x |
|
|
0 |
|
| 0 |
0 |
1 |
0 |
... |
0 |
0 |
x' |
0 |
| 0 |
0 |
0 |
1 |
... |
0 |
0 |
x" |
0 |
| 0 |
0 |
0 |
0 |
... |
0 |
0 |
x(3) |
0 |
| ... |
... |
... |
... |
... |
... |
... |
... |
... |
| 0 |
0 |
0 |
0 |
... |
0 |
1 |
x(n-2) |
0 |
| -a0 |
-a1 |
-a2 |
-a3 |
... |
-an-2 |
-an-1 |
x(n-1) |
b |
 |
|
 |
 |
|
 |
 |
|
 |
The first n-1 components in the equation X' = AX+B
merely define each component of X as the derivative of the previous one,
whereas the last component expresses
the original high-order differential equation.
Now, the general discussion above applies
fully with a W matrix whose first line consists of n independent solutions of the
homogeneous equation (each subsequent line is simply the derivative of its predecessor).
Here comes the Green function...
However, we are only interested in the first component of X.
This simplifies things greatly. We don't have to work out every component of
W-1.
In fact, looking at the above boxed formula, we see that we only need the first component
of W(t)W-1(u)B(u) which may be written G(t,u)b(u),
by calling G(t,u) the first component of
W(t)W-1(u)Z, where Z is a vector whose component are all zero,
except the last one which is one.
This function G(t,u) is called
the Green function associated to the given homogeneous equation. It has a simple
expression (given below) in terms of a ratio of determinants computed for independent
solutions of the homogeneous equation.
(Such an expression makes it easy to prove that
the Green function is indeed associated to the equation itself and not to a particular
set of independent solutions, as it is clearly invariant if you replace any solution by
some linear combination in which it appears with a nonzero coefficient.)
For a third-order equation with homogeneous solutions A(t), B(t) and C(t), the expression of
the Green function (which generalizes to any order) is simply:
G(t,u) =
|
|
 |
A(u) |
B(u) |
C(u) |
 |
|
| A'(u) |
B'(u) |
C'(u) |
| A(t) |
B(t) |
C(t) |
 |
 |
 |
| |
 |
A(u) |
B(u) |
C(u) |
 |
|
| A'(u) |
B'(u) |
C'(u) |
| A"(u) |
B"(u) |
C"(u) |
It's also a good idea to define G(t,u) to be zero when u>t,
since such values of G(t,u) are not used in the integral
ò t G(t,u) b(u) du.
This convention allows us to drop the upper limit of the integral,
so we may write a special solution of the inhomogeneous equation
as the definite integral
(from -¥ to +¥,
whenever it converges):
ò G(t,u) b(u) du.
If this integral does not converge (the issue may only arise when u goes to
-¥), we may still use this formal expression by considering
that the forcing term b(u) is zero at any time t earlier than whatever happens to be the
earliest time we wish to consider.
(This is one unsatisfying way to reestablish some kind of
fixed arbitrary lower bound for the integral of interest when the only natural one,
namely -¥, is not acceptable.)
In the case of the equation x''' - 3x" + 4x = exp(2t), three independent solutions are
A(t) = exp(-t),
B(t) = exp(2t), and
C(t) = t exp(2t). This makes the denominator in the above (the "Wronskian")
equal to 9 exp(3u) whereas the numerator is
(3t-3u-1)exp(u+2t)+exp(4u-t).
With those values, the integral of G(t,u)exp(2u)(u)du when u goes from 0 to t
turns out to be equal to
f(t) = [ (9t2-6t+2)exp(2t) - 2 exp(-t) ]/54, which is therefore a
special solution of your equation. The general solution may be expressed as:
x(t) = (a + bt + t2/6) exp(2t) + c exp(-t)
[ a, b and c are constant ]
Clearly, this result could have been obtained without this heavy artillery:
Once you've solved the homogeneous equation and
realized that the forcing term is a solution of it,
it is very natural to look for an inhomogeneous solution of the form
z exp(2t) and find that z"=1/3 works.
That's far less tedious than computing and using the associated Green's function.
However, efficiency in this special
case is not what the question was all about...
(2001-04-13)
Convolutions and the Theory of Distributions
An introduction to the epoch-making approach of Laurent Schwartz.
-
The above may be dealt with using the elegant idea of
convolution products among distributions.
The notorious Theory of Distributions occurred to the late
Laurent
Schwartz (1915-2002) "one night in 1944".
For this, he received the first
Fields Medal
ever awarded to a Frenchman, in 1950.
 (Schwartz taught this writer Hilbertian Analysis
in the Fall of 1977.)
(Schwartz taught this writer Hilbertian Analysis
in the Fall of 1977.)
A linear differential equation with constant coefficients
(an important special case) may be expressed as a convolution
a * x = b.
The convolution operator * is bilinear,
associative and commutative.
It has an identity element, the so-called
Delta distribution d,
also known as Dirac's "function".
Loosely speaking the Delta distribution d
would correspond to a "function" whose integral is 1,
but whose value at every point except zero is zero.
The integral of an ordinary function which is zero almost everywhere
would necessarily be zero.
Therefore, the d distribution cannot possibly
be an ordinary function: Convolutions must be put in the proper context of the
Theory of Distributions.
A strong case can be made that the convolution product is the notion that gives rise
to the very concept of distribution.
Distributions had been used loosely by physicists for a long time, when
Schwartz finally found a very simple mathematical definition for them:
Considering a (very restricted) space D of so-called test functions,
a distribution is simply a linear function which associates a scalar
to every test function.
Although other possibilities have been studied (which give rise to less
general distributions) D is normally the so-called Schwartz space
of infinitely derivable functions of compact support
These are perfectly smooth functions vanishing outside of a bounded domain,
like the function of x which is
exp(-1 / (1-x 2 ))
in [-1,+1] and 0 elsewhere.
What could be denoted f(g) is written
f*g instead.
This hint of an ultimate symmetry between the rôles of f and g
is fulfilled by the following relation, which holds whenever the integral exists
for ordinary functions f and g.
[f*g](t) =
ò f(t-u)g(u) du
This relation may be used to establish commutativity
(switch the variable to v = t-u, going from
+¥ to -¥
when u goes from
-¥ to +¥).
The associativity of the convolution product is obtained
by figuring out a double integral.
Convolutions have many stunning properties.
In particular, the Fourier transform of the convolution product of two functions is
the ordinary product of their Fourier transforms.
Another key property is that the derivative of a convolution product may be obtained
by differentiating either one of its factors:
(f*g)'
=
f '*g
=
f*g'
This means the derivatives of a function f can be expressed as convolutions, using
the derivatives of the d distribution
(strange but useful beasts):
f = d * f
f' = d'
* f
f'' = d''
* f
etc.
If the n-th order linear differential equation
discussed above has constant coefficients,
we may write it as f*x = b
by introducing the distribution
f = d(n) +
an-1 d(n-1) + ... +
a3 d(3) +
a2 d" +
a1 d' +
a0 d
Clearly, if we we have a function such that
f*g=d,
we will obtain a special solution of the inhomogeneous equation as
g*b.
If you translate the convolution product into an integral, what you obtain is thus
the general expression involving a
Green function G(t,u)=g(t-u),
where g(v) is zero for negative values of v.
The case where coefficients are constant is therefore much simpler than
the general case:
Where you had a two-variable integrator, you now have a single-variable one.
Not only that, but the homogeneous solutions are well-known
(if z is an eigenvalue
of multiplicity n+1 for the matrix involved, the product of exp(zt) by any polynomial of
degree n, or less, is a solution).
In the important special case where all the eigenvalues are
distinct, the determinants involved in the expression of
G(t,u)=g(t-u) are essentially Vandermonde determinants, or Vandermonde cofactors
(a Vandermonde determinant is a determinant where each column consists of the successive
powers of a particular number).
The expression is thus fairly easy to work out and may be put into the following simple form,
involving the characteristic polynomial P for the equation
(it's also the characteristic
polynomial of the matrix we called A in the above).
For any eigenvalue z, the derivative P'(z)
is the product of the all the differences between
that eigenvalue and each of the others (which is what Vandermonde expressions entail):
g(v) =
exp(z1v) / P'(z1) +
exp(z2v) / P'(z2) + ... +
exp(znv) / P'(zn)
if v>0
With this, x = g*b is indeed
a special solution of our original equation f*x = b
brentw
(Brent Watts of Hickory, NC.
2001-05-05)
Laplace Transforms
How
do you use Laplace transforms to solve the following system
of differential equations [with the initial conditions below]:

- w" + y + z = -1
- w + y" - z = 0
- -w' -y' + z"=0
Initial conditions (when t=0): w=0, w'=1, y=0, y'=0, z= -1, z'=1.
The (unilateral) Laplace transform g(p) of a function f(t) is defined via
g(p) = òo¥ f(t) exp(-pt) dt ,
for any positive p, whenever this integral makes sense.
For example, the Laplace transform of a constant k is the function g such that
g(p)=k/p.
The most important property of the Laplace transform is obtained by
integrating by parts
f '(t) exp(-pt) dt and relates the Laplace transform
L(f ') of f ' to the
Laplace transform L(f) of f via: L(f ')[p] =
-f(0) + p L(f)[p].
This may be iterated:
L(f")[p] = -f '(0) + p L(f ')[p] =
-f '(0) - p f(0) + p2 L(f)[p], etc.
This is the basis of the so-called Operational Calculus, invented by
Oliver Heaviside (1850-1925), which translates many practical systems of differential
equations into algebraic ones.
(Originally, Heaviside was interested in the transient solutions to the simple differential
equations arising in electrical circuits).
In this particular case, we may use capital letters to denote Laplace transforms of
lowercase functions (W=L(w), Y=L(y), Z=L(z)...)
and your differential system translates into:
- (p2 W - 1 - 0p)+ Y + Z = -1/p
- W + (p2 Y - 0 - 0p) - Z = 0
- -(pW - 0) -(pY - 0) + (p2 Z - 1 + p) = 0
In other words:
- p2 W + Y + Z = 1 -1/p
- W + p2 Y - Z = 0
- -pW -pY + p2 Z = 1-p
Solve for W,Y and Z and express the results as simple sums
(that's usually the tedious part,
but this example is clearly designed to be simpler than usual):
- W = 1/(p2 +1)
- Y = p/(p2 +1) - 1/p
- Z = 1/(p2 +1) - p/(p2 +1)2
The last step is to go from these Laplace transforms back to the original
(lowercase) functions of t, with a reverse lookup using a table of
Laplace transforms, similar to the (short) one provided below.
- w = sin(t)
- y = cos(t) - 1
- z = sin(t) - cos(t)
With other initial conditions, solutions may involve various linear combinations
of no fewer than 5 different types of functions
(namely: sin(t), cos(t), exp(-t), t and the constant 1),
which would make a better showcase for Operational Calculus than this
particularly simple example...
Below is a small table of Laplace transforms. This table enables a reverse lookup
which is more than sufficient to solve the above for any set of initial conditions:
Function
f(t) |
Laplace transform
g(p)
= òo¥ f(t) exp(-pt) dt |
| 1 = t 0 | 1/p |
| t | 1/p2 |
| t n | n! / pn+1 |
| exp(at) | 1 / (p-a) |
| sin(kt) | k / (p2 + k2 ) |
| cos(kt) | p / (p2 + k2 ) |
| exp(at) sin(kt) | k / ([p-a]2 + k2 ) |
| exp(at) cos(kt) | [p-a] / ([p-a]2 + k2 ) |
| d [Dirac Delta] | 1 |
| f '(t) | p g(p) - f(0) |
| f ''(t) | p2 g(p) -
f(0) -
p f '(0) |
brentw (
Brent Watts of Hickory, NC.
2001-03-19)
1) What is an example of a function for which the integral from
-¥ to +¥
of |f(x)| dx exists, but [that of] of f(x)dx does not?
2) [What is an example of a function f ] for which the opposite is true?
The integral from
-¥ to +¥
exists for f(x)dx but not for |f(x)|dx .
1) Consider any nonmeasurable set E within the interval [0,1]
(the existence of such a set is guaranteed by Zermelo's
Axiom of Choice)
and define f(x) to be: - +1 if x is in E
- -1 if x is in [0,1]
but not in E
- 0 if x is outside [0,1]
The function f is not Lebesgue-integrable,
but its absolute value clearly is (|f(x)| is equal to 1 on [0,1] and
0 elsewhere).
That was for Lebesgue integration. For Riemann integration, you may construct a simpler
example by letting the above E be the set of rationals between 0 and 1.
2) On the other hand, the function sin(x)/x is a simple example of a function
which is Riemann-integrable over
]-¥,+¥[
(Riemann integration can be defined over an infinite interval,
although it's not usually done in basic textbooks),
whereas the absolute value |sin(x)/x| is not.
Neither function is Lebesgue-integrable over
]-¥,+¥[,
although both are over any finite interval.
araimi
(2001-04-10)
Show that: f (D)[eax y] = eax f (D+a)[y] ,
where D is the operator d/dx.
If your notation is what I think it is, it requires some explaining for most readers:
If f (x) is the converging sum
of all terms
an xn
(for some scalar sequence
an ),
f is called an analytic function
[about zero] and it can be defined
for some nonnumerical things that can be added,
scaled or "exponentiated"...
If M is a finite square matrix representing some linear operator
(which we may also call M),
f (M) is defined as a power series of M.
If there's a vector basis in which the operator M is diagonal,
f (M) is diagonal
in that same basis, with f (z) appearing on the diagonal of f (M)
wherever z appears in the diagonal of M.
Now, the differential operator D is a linear operator like any other,
whether it operates on a space of finitely many dimensions
(for example, polynomials of degree 57 or less) or infinitely many dimensions
(polynomials, formal series...).
f (D) may thus be defined the same way.
It's a formal definition which may or may not have a numerical counterpart,
as the formal series involved may or may not converge.
The same thing applies to any other differential operator,
and this is how I interpret f (D) and f (D+a)
in the above question.
To prove that a linear relation holds when f appears homogeneously
(as is the case here),
it is enough to prove that it holds for any n
when f (x)=xn :
- The relation is trivial for n=0
(the zeroth power of any operator is the identity operator) as the relation translates
into exp(ax)y = exp(ax)y.
- The case n=1 is:
D[exp(ax)y] = a exp(ax)y + exp(ax)D[y] = exp(ax)(D+a)[y].
- The case n=2 is obtained by differentiating the case n=1 exactly like the case n+1 is
obtained by differentiating case n, namely:
Dn+1[exp(ax)y] = D[exp(ax)(D+a)n(y)]
= a exp(ax)(D+a)n[y] + exp(ax) D[(D+a)n(y)]
= exp(ax) (D+a)[(D+a)n(y)] = exp(ax) (D+a)n+1[y].
This completes a proof by induction for any f (x) = xn,
which establishes the relation for any analytic function f,
through summation of such elementary results.
|
|
 |

 In theory, a rocket vehicle could have a very large acceleration at the very beginning and
almost nothing after a small fraction of a second.
When that's the case the distance would be (almost) twice the above distance.
In theory, a rocket vehicle could have a very large acceleration at the very beginning and
almost nothing after a small fraction of a second.
When that's the case the distance would be (almost) twice the above distance.
 The opposite (silly) case is when you push by hand the above rocket vehicle for more than
4 seconds (moving it only a few feet, a few inches, or nothing at all),
then the rocket fires up and reaches 60 mph in a fraction of a second,
having traveled only a short distance in the process...
The opposite (silly) case is when you push by hand the above rocket vehicle for more than
4 seconds (moving it only a few feet, a few inches, or nothing at all),
then the rocket fires up and reaches 60 mph in a fraction of a second,
having traveled only a short distance in the process...