johnrp (John P. of Middletown, NJ.
2000-10-14)
Can you rearrange the following infinite series so that its sum equals 43?
1 -1/2 +1/3 -1/4 +1/5 -1/6 +1/7 -1/8 +1/9 -1/10 ...
-
Yes. In fact such a thing can be done for any "target sum" S (here S=43) with any series
which is convergent but not absolutely convergent (that is, the series of absolute values
does not converge). So let's do this in general terms rather than focus on the special case:
Take as many positive terms of the series as strictly necessary to exceed S
(that's always possible, as explained below), then take as many negative terms to have the
partial sum fall below S, then use positive terms again to go above S, switch to negative
terms to go below S again, etc.
Note that, as advertised above, it is always possible to add enough terms of the series to
make up for any (positive or negative) difference between the current sum and the target S.
That's because the series of the absolute values is divergent (so both the series
of negative terms and the series of positive terms must be divergent, or else the whole
series would not be convergent).
In this process (at least after the first step) the difference between S and any partial sum
is never more than the magnitude of the term added at the latest "switch" from negative to
positive (or vice-versa).
Since the magnitudes of such terms tends toward zero, partial sums tend toward S.
S is therefore the sum of the "rebuilt" series.
Now, for the benefit of any reader who may not be familiar with the properties of the
so-called "harmonic" series involved here, we shall prove (as is required to apply the
above in this special case) that the following series does diverge:
1+1/2+1/3+1/4+1/5+1/6+1/7+1/8+1/9+1/10+...
One elementary way to do so is to remark that
the series is bounded from below by the series obtained by replacing 1/n with 1/p,
where p is the lowest power of 2 greater than or equal to n:
1+1/2+1/4+1/4+1/8+1/8+1/8+1/8+1/16+1/16+...
By grouping equal terms in this sum, we see that the partial sum
up to the term of rank n=2p is simply equal to 1+p/2.
The partial sums of the original series up to the same rank are therefore no less than 1+p/2
as well. This means that such partial sums will eventually exceed any preset goal,
no matter how high. The series diverges (rather slowly, though)... QED.
[The above method is attributed to
Nicole
Oresme, who published the remark around 1350.]
 (Brent Watts of Hickory, NC.
2001-04-13)
(Brent Watts of Hickory, NC.
2001-04-13)
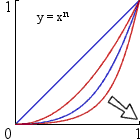
How do you show that the sequence
fn : x ® xn
converges for each x in the closed interval [0,1]
but that the convergence isn't uniform?
-
The simple convergence of a sequence of functions is just pointwise convergence.
In this case, the limit of xn is clearly 0 when x is in [0,1[ and 1 when x=1.
Your sequence of function fn thus converges and its limit is
the function f defined over [0,1] which is zero everywhere except at point 1,
where f(1)=1.
Now, simple convergence does not tell you much about the limit.
The limit of continuous functions may not be continuous (this is what happens here).
Worse, the integral of the limit may not be equal to the limit of the integrals:
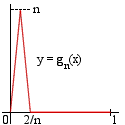 Consider, for example, the sequence of functions gn on [0,1]
for which gn(x) is n2x when x is in [0,1/n],
n(2-nx) when x is in [1/n,2/n] and zero elsewhere.
The pointwise limit of gn(x) is always zero (x=0 included,
since gn(0)=0 for any n).
Yet, the integral of gn is always equal to 1, for any n≥2.
Consider, for example, the sequence of functions gn on [0,1]
for which gn(x) is n2x when x is in [0,1/n],
n(2-nx) when x is in [1/n,2/n] and zero elsewhere.
The pointwise limit of gn(x) is always zero (x=0 included,
since gn(0)=0 for any n).
Yet, the integral of gn is always equal to 1, for any n≥2.
This is why the notion of uniform convergence was introduced: We say that a sequence
of functions fn defined on some domain of definition D converges
uniformly to its limit f when it's always possible for any positive quantity
e to exhibit a number N(e) such
that whenever n is more than N(e), the quantity
|fn(x)-f(x)| is less than e,
for any x in D. (Note that a "domain of definition" is not necessarily a "domain"
in the sense of an open region, ita est. Whenever it's critical, make sure to specify
which meaning of "domain" you have in mind.)
Uniform convergence does imply that the integral of the
(uniform) limit is the limit of the integrals. It also implies that the (uniform) limit
of continuous functions is continuous.
Since you have a discontinuous limit here, the convergence can't possibly be uniform...
The above is enough to answer your question, but you may also want
(for educational purposes) to show directly that it's not possible for a given
(small enough) quantity e>0
to find an N such that fn(x) is within e
of its limit for any x whenever n≥N.
This is so because, for 0<e<1,
any x in [e1/n,1[
is such that fn(x) is more than
e away from the (zero) limit at this point.
brentw (
Brent Watts of Hickory, NC.
2000-12-07)
What is the definition of a Cauchy sequence? [...]
-
A Cauchy sequence is a sequence U for which,
given any small positive quantity e,
there is some integer N(e) such that,
for any p and q both larger than N(e),
|U(p)-U(q)| is less than e.
A convergent sequence is always a Cauchy sequence.
The converse is only true in a complete space (like the Real Numbers);
it's not true for the rationals.
In fact a complete metric space can be defined as a space
in which every Cauchy sequence converges...
One usually defines real numbers, as equivalence classes of
rational Cauchy sequences
(U and V being equivalent if the limit of U(n)-V(n) is zero).
On 2001-03-11,
Brent asked for:
[A specific] example of how to prove whether a given sequence is a Cauchy sequence or not.
|
In the realm of real numbers, proving that a sequence converges and proving it's a
Cauchy sequence are just two aspects of the same thing. Therefore, we will choose an example
of a sequence in the the field of rationals (a notoriously incomplete space,
as was first glimpsed by Pythagoras about 2500 years ago):
Consider the rational sequence u, recursively defined via:
u(0)=1 and u(n+1) = u(n)/2 + 1/u(n)
u(1)=3/2 u(2)=17/12 u(3)=577/408 u(4)=665857/470832 etc.
First you may want to prove that u(2n) is an increasing sequence and that
u(2n+1)
is a decreasing one, whereas u(2m+1) is greater than any u(2n) for any pair n,m.
With the additional remark that u(2n+1)-u(2n) tends toward zero as n tends to
infinity, you've got all the ingredients to prove that, for p and q greater than n,
|u(p)-u(q)| is less than |u(n)-u(n+1)| and thus tends to zero when n tends to infinity.
In other words, the sequence u is a rational Cauchy sequence.
This should come as no surprise to anyone who knows about the irrational limit
of u (namely Ö2),
a "special" number which was not at all taken for granted 2500 years ago:
The irrationality of what is still sometimes referred to as the constant of Pythagoras
is said to have prompted
the sacrifice to the gods of 100 oxen (a so-called hecatomb)...
brentw
(Brent Watts of Hickory, NC. 2001-04-14)
[...] Explain the concept of Darboux integrals.
-
Before Lebesgue took a radically different (and better) approach to the problem of defining
integrals, there were a succession of definitions which all involved dividing an interval
of integration [a,b] into a finite number of segments with extremities xk such that
a=x0<x1< ... <xn=b.
The length (xk+1-xk) of each segment is less than a
given positive quantity e.
A certain finite sum is then computed for a given function f
(see below for the main types of such sums),
if the sum has a limit as e tends to zero,
regardless of the chosen subdivisions, then the function f is said to be integrable
and the limit is said to be its integral (in the sense of Cauchy, Riemann, Darboux, etc.).
Historically, such definitions have been based on several types of sums,
including:
- Cauchy:
å (xk+1-xk)
f(xk) [This definition is now obsolete]
- Riemann:
å (xk+1-xk)
f(sk)
where sk may be anywhere between xk and xk+1
- Darboux (lower):
å (xk+1-xk)
Lk
where Lk is the
greatest lower bound of f(x) for x in [xk+1-xk]
- Darboux (upper):
å (xk+1-xk)
Uk
where Uk is the
least upper bound of f(x) for x in [xk+1-xk]
The last two sums correspond to the lower and upper Darboux integrals.
The nice thing is that a function f is Riemann-integrable
if and only if
its lower Darboux integral equals its upper Darboux integral.
What Lebesgue did, of course, was to realize that slicing the "area"
delimited by a function into horizontal slices rather than vertical ones
would lead to a notion of integral that is far more general (the Lebesgue Integral),
provided you define carefully the "measure" of such horizontal slices,
which may be quite complex... But that is another story altogether,
which has little to do with Darboux.
 brentw
( Brent Watts of Hickory, NC.
2000-11-25)
brentw
( Brent Watts of Hickory, NC.
2000-11-25)
How do I evaluate the Fourier series of the function
f(x)= x(2p-x)
in the interval 0 < x < 2p ?
The Fourier expansion of a function
f(x) = [f(x-) + f(x+)] / 2
of period 2p is:
f(x)
|


 |
|
ao |
|
 |
|
|
|
[ an cos(nx) + bn sin(nx) ]
|
|
 |
 |


 |
2 |
 |
The coefficients an and bn are twice the
average values of cos(nx) f(x) and sin(nx) f(x), respectively.
They are given by Euler's formulas :
|
For an even function, like the one at hand, the b-coefficients are all
zero and we are only concerned with the first formula, giving the a-coefficients.
(Conversely, the a-coefficients would all be zero for an odd function.)
In this case, all you have to do is integrate by parts twice over the interval
0 to 2p when n is nonzero, whereas the case
n = 0 is trivial
(it's all about integrating a quadratic function).
So, an is -4/n2 if n is nonzero,
whereas ao is
4p2/3.
All told:
x (2p-x)
|


 |
2p2 |
|
4
|
|
|
|
cos(nx) |
[ For x between 0 and 2p ] |
|
 |
 |
 |


 |
3 |
|
n2 |
| p2 |


 |
|
|
1 |
|
You may want to remark that, for x = 0, the above translates
into a proof of a famous result due to Euler (1735): The sum
of the reciprocals of all nonzero perfect squares is
p2/6 ...
|
 |
|
 |
| 6 |


 |
n2 |
Finding the exact value of this sum was an infamous question,
 first posed by
Pietro
Mengoli in 1644, called the
Basel Problem
after the hometown of Jacob
Bernoulli, who was first in a long list of notorious mathematicians (including
Leibniz)
who failed to discover the above solution.
first posed by
Pietro
Mengoli in 1644, called the
Basel Problem
after the hometown of Jacob
Bernoulli, who was first in a long list of notorious mathematicians (including
Leibniz)
who failed to discover the above solution.
brentw (
Brent Watts of Hickory, NC.
2001-03-05)
How does one prove [this relation]?
-
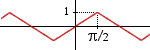
Consider the odd function f(x) of period 2p
with an axis of symmetry at x=p/2 and equal to
2x/p when x is between 0 and p/2
(so that f(p/2)=1).
Its Fourier expansion may be obtained with Euler's formulas:
f(x)
|


 |
8 |
|
|
|
(-1)n |
sin(2n+1)x
|
|
 |
 |


 |
p2 |
(2n+1)2 |
Integrate that to obtain the expansion of a primitive g(x) of f(x), namely:
g(x)
|


 |
C
|
|
8 |
|
|
|
(-1)n |
cos(2n+1)x
|
|
 |
 |
 |


 |
|
p2 |
(2n+1)3 |
The constant C is equal to the average of g(x) over one complete period.
It depends on which value we choose for g(0).
With g(0)=0, we have
g(x)=x2/p
for x between 0 and p/2.
Because of the symmetry about x=p/2,
the average C is clearly
C=g(p/2)=p/4.
Plug this value of C in the above relation at point x=0 (where g(x)=0 and cos((2n+1)x)=1),
and you do obtain the value
p3/32
for the sum you were trying to evaluate.
Consider the following expression, which generalizes the above.
We are only concerned with integral (positive) values of k,
but it should be noted that the function
b, which is called Dirichlet's Beta Function,
may be defined by analytic continuation over the entire complex plane.
It has no singularities.
The above shows that
b(3) =
p3/32.
Differentiating f(x), instead of integrating it, would have given
b(1) = p/4,
a result which is commonly obtained by computing the value of the
arctangent function at x=1, using its Taylor expansion about 0.
It is worth noticing that the above method may be carried further with
repeated integrations.
Every other time, such an integration gives an
exact expression for the alternating sum of some new power of the
reciprocals of odd integers.
In other words, we obtain the value of
b(k) for any odd k, and it happens to be a rational
multiple of p k:
| b(1) = p/4 |
The general expression is
b(2n+1)
|


 |
|
(p/2) 2n+1 |
| E2n |
|
|
 |


 |
2(2n)! |
|
| b(3) = p3/32 |
| b(5) = 5p5/1536 |
| b(7) = 61p7/184320 |
| b(9) = 277p9/8257536 |
| b(11) = 50521p11/14863564800 |
In this, | E2n | is an integer. The Euler number
En is the coefficient of zn/n! in the Taylor expansion of
1/ch(z) [where ch is the hyperbolic cosine function;
ch(z) = (ez +e-z )/2].
Starting with n = 0, the sequence of Euler numbers is:
1, 0, -1, 0, 5, 0, -61, 0, 1385, 0, -50521, 0, 2702765, 0,
-199360981, 0,
19391512145, 0, -2404879675441, 0,
370371188237525, 0, ...
We may also consider the secant function 1/cos(z)
which has the same expansion as
1/ch(z) except that all the coefficients are positive, so that:
¼ px
/ cos(½ px)
=
å n
b(2n+1) x 2n+1
There does not seem to be any similar expression for even powers. In fact,
b(2) is currently defined as an independent
fundamental mathematical constant, the so-called
Catalan Constant:
G = 0.915965594177219015...
This is the exact opposite of the situation for nonalternating sums, where
even powers correspond to an exact expression in terms of a rational multiple of the
matching power of p, whereas odd powers do not...
brentw (
Brent Watts of Hickory, NC.
2000-11-21)
How do you prove the following relation?
(p2/ab)
coth(pa) coth(pb)
|


 |
|
|
|
|
1 |
|
 |


 |
(m2 + a2 ) (n2 +
b2 ) |
-
The relation
åm ån u(m) v(n)
=
[ åmu(m) ]
[ ånv(n) ]
holds whenever the series involved are absolutely convergent
(which is clearly the case here).
Therefore, we only have to establish the following simpler equality:
The sum on the right-hand side looks like a series of Fourier coefficients.
For what periodic function?
Well, it's not difficult to see that the correct denominator is obtained
for the continuous even function of period 2p
which equals cosh(ax)
if x is in the interval [-p,p].
When x is in that interval, the Fourier expansion may be written in two equivalent
form (defining a-m to be equal to am ):
cosh(ax)
|


 |
|
ao |
|
 |
|
|
|
am cos(mx) =
½
|
|
am cos(mx)
|
|
 |
 |


 |
2 |
 |
With Euler's formula, you obtain
am =
[2a(-1)m/p]
sinh(pa) / (m2 + a2 ).
At the point x = p,
we have cos(mx)= (-1)m
and the above relation thus translates into the desired equality
[just divide both sides of the relation by
(a/p)
sinh(pa)].
brentw (
Brent Watts of Hickory, NC.
2001-04-14)
How do you use the Fourier series for the function
f(x) = ex for x in ]0,2p[
to find the sum [S] of the series 1/(k2 + 1) ?
[ k=1 to ¥ ]
-
Use Euler's formulas to compute the Fourier coefficients of f(x).
Note that if you consider f as a function of period
2p equal to exp(x) in
]0,2p[,
it has a jump discontinuity at any point x=2np
(where n is any integer).
This means (and it's important for the rest)
that the Fourier series converge to the half-sum of the left limit and the right limit
at such points of discontinuity,
in particular the value at point 0 is
[exp(2p)+1]/2.
Now, the computation of the Fourier coefficients is easy if you notice that
exp(x)cos(kx) and exp(x)sin(kx)
are the real and imaginary parts of exp((1+ki)x)
(it's clear we will only need the real part, but I'll pretend I did not notice).
The indefinite integral of that is simply
exp((1+ki)x)/(1+ki), which we may also express as
exp((1+ki)x) (1-ki)/(1+k2).
The definite integral from 0 to 2p is thus
(exp(2p)-1)(1-ki)/(1+k2),
and the Fourier coefficients are obtained by multiplying this by
1/p and using the real and imaginary part separately.
All told:
f(x) =
[exp(2p)-1]/p
(½ + SUM[ k=1 to ¥,
(cos(kx) - k sin(kx))/(1+k2) ] )
All you have to do is apply this to x=0
(this is why we did not really need the coefficients of sin(kx)).
With the above remark to the effect that the LHS really represents
[f(x-)+f(x+)]/2 at any jump discontinuity like x=0, we obtain:
[exp(2p)+1] / 2 =
[exp(2p)-1] / p ( ½ + S )
where S is the sum you were after. Therefore:
S = p/2 - ½ + p /
[ exp(2p)-1 ] = 1.076674047...
This is also a special case (a = 1) of the relation established
above in the form:
p coth(p) = 1 + 2 S
brentw (
Brent Watts of Hickory, NC.
2000-11-28)
[...] Please explain the Gibbs phenomenon of Fourier series.
-
At a point x where a function f has a jump discontinuity, any partial sum of
its Fourier series adds up to a function that has an "overshoot"
(i.e., a dampened oscillation) whose initial amplitude is about 9%
of the value of the jump J=|f(x+)-f(x-)|.
This amplitude is not reduced by adding more terms of the Fourier series.
It's not difficult to prove that, with n terms, the maximum value of the overshoot
occurs at/near a distance of p/2n on either side of x.
(You may do the computation with any convenient function having a jump J;
I suggest f(x)=sign(x)J/2 between
-p and p.
Adding a continuous function to that would put you back to the "general"
case without changing the nature or amplitude of the Gibbs oscillations.)
When n tends to infinity, the maximum reached by the first overshoot
oscillation is about 8.948987% of the jump J.
This value is precisely (2G/p-1)/2,
where G is known as the Wilbraham-Gibbs Constant:
| G | = |
óp
õ0 |
sin(q)/q dq |
| = |
1.8519370519824661703610533701579913633458... |
This is sometimes called "the 9% overshoot",
as it is about 9% of the total jump J.
[It's 18% (17.89797...%) when half the jump (J/2) is used as a unit.]
This tells you exactly what kind of convergence is expected from a Fourier series
about a discontinuity of f.
For a small h, you can always increase the number of Fourier terms to that Gibbs
oscillations are mostly confined to the very beginning of the interval [x,x+h].
This is somewhat like the convergence to zero of the sequence of functions
f(n,x)
defined as being equal to 4nx(1-nx) for x between 0 and 1/n, and zero elsewhere.
f(n,x) always reaches a maximum value of 1 for x=1/2n.
f(n,x) does converge to zero, but it is not uniform convergence!
Same thing with partial Fourier sums in a neighborhood of a jump discontinuity...
brentw (
Brent Watts of Hickory, NC.
2000-12-08)
What is the Cauchy principal value (PV) of an integral?
-
If f has no singularities, the principal value (PV) is just the ordinary integral.

If the function f has a single singularity q between a and b
(a<b),
the Cauchy principal value of its integral from a to b is the limit
(whenever it exists),
as e tends to 0+, of the sum of the integral from
a to q-e
and the integral from q+e to b. Also, if the interval
of integration is ]-¥,+¥[ with a
singularity at ¥ the principal value is the limit,
whenever its exists, of the integral in the interval ]-A,+A[ as A tends to infinity.
When f has a discrete number of singularities between a and b
(a and b excluded, unless both are infinite),
the PV of its integral may be obtained by
splitting the interval [a,b] into a sequence of intervals each containing
a single singularity. The above applies to each of these, and the PV of the integral
over the entire interval is obtained by adding the principal values over all such
subintervals.
The fact that the principal value is used may be indicated by the letters PV
before the integral sign, or by crossing with a small horizontal dash the integral sign
(see illustration above).
However, it is more or less universally understood that the Cauchy principal
value is used whenever needed, and some authors don't bother to insist on this
with special typography.
brentw (
Brent Watts of Hickory, NC.
2000-11-21)
How do I solve the differential equation
2(1-x)y" + (1+x)y' + [x - 3 - (x-1)2exp(x)]y = 0
about the pole x=1?
-
The singularity at x=1 is a "regular" one (this means simply that if the coefficient
of y" is normalized to 1, the coefficient of y' has at most a single pole
at x=1 and the coefficient of y has at most a double pole at x=1).
Therefore, the method of Froebenius is applicable.
It consists in finding a solution in the form of a so-called Froebenius series
of the following form (where h=x-x0 in general, and h=x-1 here) with a(0) nonzero:
y = hm [ a(0) + a(1) h + a(2) h2 + a(3) h3 + ... ]
In the above, m is not necessarily an integer, so that a Froebenius series
is more general than either a Taylor series (for which m is a natural integer)
or a Laurent series (for which m is any integer).
In the DE we're asked to study, we have:
-2h y" + (2+h) y' + [h-2-h2exp(1+h)] y = 0
The method of Froebenius is simply to expand the above LHS in terms
of powers of h to obtain a sequence of equations that will successively give
the values of a=a(0), b=a(1), c=a(2), d=a(3), etc.
Let's do it.
The above LHS is hm-1 multiplied by:
[-2am(m-2)] +[a(m-2)-2b(m2-1)]h +[a+b(m-1)-2cm(m+2)]h2 +O(h3)
We have to successively equate to zero all the square brackets.
Since a is nonzero, the first square bracket gives us the acceptable value(s)
of the index m (this is a general feature of the method and this first
critical equation is called the indicial equation).
Generally, the indicial equation has two roots (for a second-degree DE)
and this gives you a pair of independent solutions.
Usually, when the roots differ by an integral value (like here)
you've got (somewhat) bad news, since the Froebenius method is only guaranteed to
work for the "larger" of the two values of m.
However, "by accident" you're in luck here:
The case m=0 gives b=a (second bracket).
Then, the third bracket gives zero for the coefficient of c
(that's the usual problem you encounter after N steps
when starting with the smaller root, if the two roots differ by N)
but it so happens that the rest of the bracket is zero too!
(That's exceptional!) So you can continue with an arbitrary value of c
and obtain d as a linear combination of a and c using the next bracket
(which I was too lazy to work out, since I knew tough
problems could not occur past that point).
The way to proceed from here is to first use a=1 and c=0 to get the first solution
as a Froebenius series F(h),
then a=0 and c=1 to get a linearly independent solution G(h).
The general solution about the singularity x=1 is then
a F(x-1) + c G(x-1).
(You don't have to bother with the index m=2 in this particular case.)
brentw (
Brent Watts of Hickory, NC.
2000-11-21)
How do I determine the Laurent series of [a function about one of its] singular points?
[...]
-
For each singular point (or pole) zo,
you want to expand f(zo+h).
If a pole has multiplicity n,
hn f(zo+h)
is an analytic function.
Compute its Taylor expansion about h=0 and divide that series
by hn
to have the Laurent series for a particular pole.
Let me use an example where the actual computation is minimal so we can do it step by step:
Consider f(z)=1/[z(z-1)2].
There's a single pole at z=0 and a double pole at z=1. Let's look only at the double pole z=1.
First compute f(1+h) [1 is the pole; in its neighborhood h is "small"].
It's just merely a question of replacing z by (1+h). Nothing to it:
f(1+h) = 1/[(1+h)((1+h)-1)2 = 1/[(1+h)h2]
multiply this by h2 and you have an analytic function about h=0 namely:
g(h) = h2 f(1+h) = 1/(1+h)
The Taylor expansion of g is well known:
g(h) = 1 - h + h2 - h3 + h4 - h5 + ...
Since f(1+h)=g(h)/h2, divide the above by
h2 to obtain the Laurent expansion
of f(1+h) about h=0, namely:
f(1+h) = 1/h2 - 1/h + 1 - h + h2 - h3 + ...
That's the Laurent expansion of f about the pole z=1.
The so-called "residue" of f for the pole z=1 is the coefficient of 1/h in the
Laurent expansion (here, that's -1);
that's the only thing that comes into play when integrating over a closed contour.
If you want the format used in many textbook
(which I don't recommend for practical calculations),
just replace h back with (z-1) and obtain something like:
f(z) = 1/(z-1)2 - 1/(z-1) + 1 - (z-1) + (z-1)2 ...
Usually, we're only concerned with the coefficient of 1/h, which is called the
residue for that pole (here it's equal to -1). The integral of a function
along any closed contour around a certain number of poles is equal to
2pi times the sum of the residues for those poles.
This is one of the most practical tools available to compute easily many
otherwise difficult definite integrals...
ó¥
õ0 |
dx |
 |
| (1+x2 )Öx |
yourm0mz (2001-12-15)
How do you find the [following] definite integral? [...]
(I am using the positive x axis as a branch cut.)
-
When attempting to apply Cauchy's residue theorem
 [the fundamental theorem of complex analysis] to multivalued functions
(like the square root function involved here), it is important to specify
a so-called "cut" in the complex plane were the function is allowed to be discontinuous,
so that it is everywhere else continuous and single-valued.
[the fundamental theorem of complex analysis] to multivalued functions
(like the square root function involved here), it is important to specify
a so-called "cut" in the complex plane were the function is allowed to be discontinuous,
so that it is everywhere else continuous and single-valued.
In the case of the square-root function, it is not possible to give a continuous definition
valid around any path encircling the origin.
Therefore, a so-called "branch-cut" line
must be specified which goes from the origin to infinity.
The usual choice is [indeed] to use the positive x-axis for that purpose.
This choice means that, when the angle q is in
[0,2p[, the "square root" of the complex number
z = r exp(iq) is simply
Öz º Ör exp(iq/2)
(the notation Ör being unambiguous because r is a positive
real number and its square root is thus defined as the only positive
real number of which it is the square).
This definition does present a discontinuity when crossing the positive real axis
(a difficulty avoided only with the introduction of Riemann surfaces,
which are beyond the scope of our current discussion).
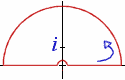 With the above definition of the square root of a complex argument,
we may thus apply the Residue Theorem to the function
f(z)=1/(1+z2)Öz on any contour which does not cross the
positive real axis.
We may choose the contour pictured at left, which does not encircle the origin
[this would be a no-no, regardless of the chosen "branch cut"]
but encloses the pole at +i when the outer circle is big enough.
With the above definition of the square root of a complex argument,
we may thus apply the Residue Theorem to the function
f(z)=1/(1+z2)Öz on any contour which does not cross the
positive real axis.
We may choose the contour pictured at left, which does not encircle the origin
[this would be a no-no, regardless of the chosen "branch cut"]
but encloses the pole at +i when the outer circle is big enough.
On the outer semicircle, the quantity |f(z)| eventually becomes much smaller
than the reciprocal of the
length of the path of integration.
Therefore, the contribution of the outer semicircle to the
contour integral tends to zero as the radius tends to infinity.
The smaller semicircle is introduced to avoid the singularity at the origin,
but its contribution to the contour integral is infinitely
small when its radius is infinitely small.
What remains, therefore, is the contribution of the two straight parts of the contour.
The integral along the right part is exactly the integral we are asked to compute,
whereas the left part contributes i times that quantity.
All told, the limit of the contour integral is (1+i) times the integral
we seek.
Cauchy's Theorem states that the contour integral equals
2pi times the sum of the residues it encircles.
In this case, there's only one such residue, at the pole i.
The value of the residue at pole i is the limit as h tends to
zero of h f(i+h), namely
1/2iÖi,
so the value of the contour integral is
pÖi = pÖ2(1+i)/2.
As stated above, this is (1+i) times the integral we want.
Therefore, the value of that integral is exactly
p/Ö2,
or about 2.221441469...
ó¥
õ0 |
xa dx |
 |
| 1 + x2 |
For what values of a does this integral converge?
What's the value of the integral when it converges?
-
The previous article deals with the special case
a = -1/2.
In general, we see that the integral makes sense in the neighborhood of zero
if a>-1 and it converges in the neighborhood of
+¥ when a<1.
All told, the integral converges when a
is in the open interval ]-1,1[.

We apply the above method to
f(z) = za/(1+z2)
[defining za with the positive x-axis as
branch cut] on the same contour (pictured at right).
The smaller semicircle is useless when a is positive and
it has a vanishing contribution otherwise
(when a>-1).
The contribution of the outer semicircle is vanishingly small also
(when a<1) because |f(z)| multiplied by the
length of the semicircle becomes vanishingly small when the radius becomes large enough.
On the other hand, the contribution of the entire positive x-axis is the integral
we are after, whereas the negative part of the axis contributes
exp(ipa) as much.
All told therefore, Cauchy's theorem tells us that our integral is
2pi/(1+exp(iap))
times the residue of f at the pole z = i.
The residue at z = i is the limit, as h tends to zero,
of h f(i+h), which is simply
exp(iap/2)/2i.
This makes the integral equal to
p exp(iap/2)/(1+exp(iap)),
which boils down to p/(2 cos ap/2),
so that we obtain:
ó¥
õ0 |
xa dx |
= |
p |
[ -1 < a < 1 ] |
 |
 |
| 1 + x2 |
2 cos (ap/2) |
We may notice that this final result is an even function of a,
which we could have predicted with the simple change of variable y = 1/x...