 |
Miscellaneous
( T. D. of Fairbanks, AK.
2000-12-04)
How do I find square roots without the use of a calculator,
especially when the square root will contain a decimal point?
( J. D. of Cape Coral, FL.
2000-12-07)
How do I extract the square root of a number?
-
It works a little bit like a long division with two basic differences:
-
Instead of one digit at a time, you handle "slices" of two digits at a time
(the pair of digits to the left of the decimal point being one such slice).
-
You get each new digit by trying at each step to "extend" twice
the previously found root with another digit to that the product of this extension
by the (largest possible) new digit does not exceed the previously computed remainder.
To make this clear, let's just compute the square root of 2:
- Remainder is 2, Root is 0, DoubleRoot is 0.
The largest digit "?" which is such that "0?" times "?" is no greater than 2 happens to be 1
(save this as the first digit in the square root). "01" times "1" is 1,
which I subract from 2, the result is 1, which gets augmented by the "next slice"
of unprocessed digits, namley "00". So, the new remainder is 100.
- Remainder is 100, Root is 1, DoubleRoot is 2.
What's the largest digit such that "2?" times "?" does not exceed 100. Well it's 4
(save this as the second digit in the root).
"24" times "4" is 96, which I subtract from 100 and augment with the next slice
of "00" digits to get 400 as the new remainder.
- Remainder is 400, Root is 1.4, DoubleRoot is 28.
The largest digit such that "28?" times "?" does not exceed 400 is 1
(which is thus our next digit).
The new remainder is 400-281=119 augmented by the next "00"; 11900 is the new remainder.
- Remainder is 11900, Root is 1.41, DoubleRoot is 282.
The next digit is 4 for which "282?" times "?" is 11296. 11900-11296 is 604;
new remainder is thus 60400.
- Remainder is 60400, Root is 1.414, DoubleRoot is 2828.
The next digit is 2 for which "2828?" times "?" is 56564. 60400-56564 is 3836;
new remainder is thus 383600.
- Remainder is 383600, Root is 1.4142, DoubleRoot is 28284.
The next digit is 1 for which "28284?" times "?" is 282841. 383600-282841 is 100759;
new remainder is thus 10075900.
- Remainder is 10075900, Root is 1.41421, DoubleRoot is 282842.
The next digit is 3 ... etc.
The square root of 2
is: 1.414213562373095048801688724209698...
 (Marc Ordower of Bryan, TX.
2000-09-22) (Marc Ordower of Bryan, TX.
2000-09-22)
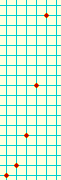
Lattice points are points of the plane with integer coordinates.
Among infinitely many lattice points,
must there always be some infinite subset of collinear points?
No. Just consider the sequence whose general term is (P,P2):
(1,1) (2,4) (3,9) (4,16) ... which does not even contain 3 collinear points.
(These are points on a parabola, but points on any infinite convex curve would do!)
(Marc Ordower of Bryan, TX.
2000-09-24)
In an infinite sequence of lattice points
where the distance [or gap] between two consecutive points is bounded...
- Is there always an infinite subset of collinear points?
- More interestingly: Must some 1000000 points be collinear?
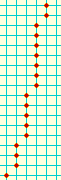 No, there need not be an infinite subset of collinear points in this case either...
Consider the sequence of points whose general term is
(floor(Ön),n):
(1,1) (1,2) (1,3) (2,4) (2,5) (2,6) (2,7) (2,8) (3,9) (3,10) ...
The distance between consecutive points is indeed bounded; it is at most equal to
Ö2.
No more than 3 points of this sequence may belong to a line that's not vertical,
while only finitely many may belong to a vertical line (namely, 2p+1 points at abscissa p).
No, there need not be an infinite subset of collinear points in this case either...
Consider the sequence of points whose general term is
(floor(Ön),n):
(1,1) (1,2) (1,3) (2,4) (2,5) (2,6) (2,7) (2,8) (3,9) (3,10) ...
The distance between consecutive points is indeed bounded; it is at most equal to
Ö2.
No more than 3 points of this sequence may belong to a line that's not vertical,
while only finitely many may belong to a vertical line (namely, 2p+1 points at abscissa p).
This does not settle the more interesting question of knowing whether there exist
for any given M (say M=1000000)
at least M collinear points in such a sequence...
(See next article.)
On 2000-09-29, Marc Ordower wrote:
I'm glad that you find this question so interesting. I had posted it in hopes that someone
would find it as appealing as I do.
However, I cannot take credit for posing this problem, as it is a classic question in
Ramsey theory.
I should also point out that the solution to this problem is known.
I'll refrain from sharing it to avoid spoiling your fun.
However, there are a great many problems along these lines which are still open.
Regards, Marc
|
References:
[Affirmative answer to the second part of the question.]
This obscure result is indeed sometimes known as the
Gerver-Ramsey theorem:
Joseph L. Gerver and L. Thomas Ramsey,
On certain sequences of lattice points, Pacific J. Math. 83 (1979) 357-363,
MR
81c:10039.
It is, in fact, enough to assume only that the gaps
[the distances between pairs of consecutive points]
are bounded on average
(which is to say that the sum of the first n gaps is less than nB,
for some positive constant B):
Carl Pomerance,
Collinear subsets of lattice point sequences--an analog of Szemerédi's theorem,
JCT-A (1980) 140-149,
MR 81m:10104.
(2000-09-29)
In the plane, an infinite sequence of lattice points
with bounded gaps contains at least M collinear points.
This is true for any integer M.
Here's my proof, which may or may not be the "classic" one which
Marc Ordower will not share...

We may assume that:
- The range of the sequence is infinite.
(Or else the result is trivial,
since at least one point must appear infinitely many times, so that infinitely
many elements of the sequence are collinear
because they are equal).
- Consecutive points are distinct.
(The theorem so restricted is clearly equivalent to the more general one).
Without loss of generality,
we may also assume that consecutive points are adjacent
(that is, they are one unit of distance apart).
If the result holds in this special case,
it holds for the general case because of the following argument:
For any sequence S of points (X(n),Y(n))
where two consecutive points are at most D units apart,
we may consider the sequence C obtained
by removing from the sequence (floor(X(n)/D),floor(Y(n)/D)) any consecutive elements which
happen to be equal.
Since C is a sequence of adjacent points, the restricted theorem implies that,
for any M, there is at least one straight line (with some rational
slope q) going through MD2 elements of C.
Well, C clearly corresponds to D by D square cells
which contain each at least one element from the original sequence S.
To the above line of
slope q corresponds a set of at most D2 lines of slope q which contain each at
least one integral point from each of those MD2 aligned cell.
The pigeonhole principle
then tells us that at least one such line contains at least M points from the original
sequence S.
In other words,
the theorem for adjacent consecutive points does imply the general case where
consecutive points are only known to be less than some distance D apart.
We now complete the proof by ...

(2005-10-25)
Ford Circles
Ford circles are named after Lester R. Ford, Sr. (1886-1975)
who introduced the concept in 1938
(American Mathematical Monthly, volume 45, number 9, pages 586-601).
The famous Ford-Fulkerson optimisation algorithm (1956) is named after his son,
Lester Randolph Ford, Jr. (who was born in 1927).
The Ford circle of the rational number p/q (expressed in lowest terms)
is the circle of diameter 1/q2 tangent
from above to the x-axis at point p/q.
Ford circles of irrational numbers are of radius 0 and reduce to a single point.
The line y = 1 is sometimes considered to be a degenerate Ford circle
of infinite radius associated with
¥ (unsigned infinity).
Remarkably, two Ford circles never overlap.
The Ford circles associated with two irreducible fractions
a/b and c/d are
tangent to each other if, and only if,
ad and bc are consecutive integers.
The largest Ford circle between such tangent Ford circles is associated
with the mediant fraction
(a+c) / (b+d).

(2005-10-25)
Farey Series
The nth Farey series is the increasing sequence of all
the rational numbers (irreducible fractions) between 0 and 1
whose denominators are n or less.
For example, the sixth Farey series is:
0, 1/6, 1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 5/6, 1
Each term of a Farey series is the mediant of the two terms that
surround it
(the three corresponding Ford circles are thus pairwise tangent).
In 1816, the geologist
John Farey,
Sen. (1766-1826) published this remark in a
short letter to
the Philosophical Magazine, entitled
"On a curious Property of vulgar Fractions".
This attracted the attention of Augustin Cauchy, who supplied a proof in
Exercises de mathématiques (1816).
Cauchy is responsible for the enduring attribution of these finite sequences to Farey.
In 1802 (14 years before Farey and Cauchy)
one C. Haros had studied the 99th Farey series,
in a paper about the approximation of decimal fractions by common fractions.

(2005-10-28)
Stern-Brocot Tree
A binary tree containing all positive rationals once and only once.
Let's label each node of a binary tree with a triplet of integers so that
the left and right offsprings of a node labeled (x,y,z) are respectively labeled
(x,x+y,y) and (y,y+z,z).
The label of the root determines the labels assigned to all the nodes.
Let's call numerator tree the tree so labeled whose root bears the label
(0,1,1).
Call denominator tree the one whose root is labeled (1,1,0).
Numerator Tree
| 0 |
1 |
1 |
| 1 | 2 |
| 1 | 2 | 3 | 3 |
| 1 | 2 | 3 | 3 | 4 | 5 | 5 | 4 |
| |
Denominator Tree
| 1 |
1 |
0 |
| 2 | 1 |
| 3 | 3 | 2 | 1 |
| 4 | 5 | 5 | 4 | 3 | 3 | 2 | 1 |
|
We use a graphical representation, where each offspring is assigned a box
half the size of its parent's.
In each box, only the middle integer of the "label" is shown.
The other two values are simply found at the top of each bounding vertical line.
(In the middle of an ascendant's box, except for a leftmost or rightmost node.)
The Stern-Brocot tree is the binary tree whose nodes are
labeled with the rational number p/q,
where p (resp. q) is the middle integer in the label of the corresponding node
of the above numerator tree (resp. denominator tree).
Remarkably, all rational numbers are thus obtained
in irreducible form.
Stern-Brocot Tree
| 1/1 |
| 1/2 | 2/1 |
| 1/3 | 2/3 | 3/2 | 3/1 |
| 1/4 | 2/5 | 3/5 | 3/4 |
4/3 | 5/3 | 5/2 | 4/1 |
The rational numbers which appear in the left half of the tree are between 0 and 1.
A Farey series is obtained when the
numbers in the first half of a line are interspersed with the numbers sitting
at the top of the box boundaries.
For example, the fourth Farey series is obtained from the last line shown above:
0, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 1
Any positive rational appears
once and only once in the Stern-Brocot tree, at a location determined by its
continued fraction expansion (CFE)...
To reach the positive rational whose CFE is
[q0,q1,q2...qn]
go q0 steps right, q1 steps left, q2 steps right, and
so forth alternately... then
go back one step (either that,
or perform only qn-1 steps in the last stage).
The Stern-Brocot tree was discovered (at least) twice:
- In 1858 by Moritz Stern
(Über eine zahlentheoretische Funktion. Crelle's Journal 55:193-220).
Moritz Abraham Stern (1807–1894) is credited with noticing the genius of his student
Bernhard
Riemann (1826-1866) early on at Göttingen.
Stern was also one of the main teachers of
Richard
Dedekind (1831-1916) who was Gauss's last student
(receiving his doctorate in 1852).
In 1858, Stern was appointed to succeed Gauss (1777-1855) as professor
ordinarius of mathematics at Göttingen University.
He was the first jewish Ordinarius
in a German university.
- In 1861, by Achille Brocot
(Calcul des rouages par approximation, nouvelle méthode.
Revue Chronométrique 3:186-194).
Achille Brocot (1817-1878) was a famous innovative clockmaker,
who stumbled upon the Stern-Brocot tree while computing optimal gear ratios.
(2005-10-29)
Eisenstein-Stern Diatomic Sequence
(A002487)
Also known as Dijkstra's "fusc" function, the sequence of the so-called
"Stern numbers" form a
recursively defined integer sequence :
b(0) = 0 , b(1) = 1 ,
b(2n) = b(n), b(2n+1) = b(n) + b(n+1)
0,1,1,2,1,3,2,3,1,4,3,5,2,5,3,4,1,5,4,7,3,8,5,7,2,7,5,8,3,7,4,5,1,6,5,9,4...
In 1982, Edsger Wybe Dijkstra
(1930-2002)
called the sequence of Stern numbers "fusc" because it possesses
a curious obfuscated property:
If the sum of two indices, n and m, is
a power of 2, then b(n) and b(m) are coprime.
The sequence of the ratios of two consecutive Stern numbers
un = b(n) / b(n+1) runs through all nonnegative
rational numbers (in reduced form) just once!
0, 1,1/2, 2, 1/3, 3/2, 2/3, 3,1/4, 4/3, 3/5, 5/2, 2/5, 5/3, 3/4, 4, ...
Moshe Newman is credited
with the discovery of a very nice alternate definition of this rational sequence,
namely:
uo = 0 and
un+1 = f (un )
where
f (x) = 1 / (1 + 2 ë x û - x )
When this sequence is displayed as
a binary tree, each level features
the same fractions as in the Stern-Brocot tree, but
at different locations:
The respective positions [0 = leftmost] of a given fraction
are mirror images in binary numeration.
Calkin-Wilf Tree
| 1/1 |
| 1/2 | 2/1 |
| 1/3 | 3/2 | 2/3 | 3/1 |
| 1/4 | 4/3 | 3/5 | 5/2 |
2/5 | 5/3 | 3/4 | 4/1 |
In this tree, the left child of a / b
is a / (a+b) ,
the right child is (a+b) / b.
Thus, if the parent fraction is in lowest terms, so are both offsprings...
References and History :
-
Gotthold
M. Eisenstein (1823-1852)
"Eine neue Gattung zahlentheoretischer Funktionen [...]" (1850)
Verhandlungen der Königlich Preussischen Akademie
der Wissenschaften zu Berlin
-
Moritz A. Stern (1807-1894)
"Über eine zahlentheoretische Funktion" (1858)
Journal für die reine und angewandte Mathematik,
55:193-220.
-
C. Giuli and R. Giuli
"A primer on Stern's Diatomic Sequence" (1979; some errors)
Fibonacci Quarterly,
17:2 (1979) 103-108, 246-248, 318-320.
-
Neil J. Calkin
and Herbert S. Wilf
"Recounting the Rationals"
[ pdf,
July 6, 1999 ]
The American Mathematical Monthly, 107
(April 2000) 360-363.
-
Igor Urbiha
"Tree of fractions and Dijkstra's fusc function"
(March 27, 2002)
Seminar on Number Theory and Algebra, University of Zagreb.
-
Jeremy Gibbons, David Lester and Richard Bird
"Enumerating the Rationals"
[ pdf ]
(2005-10-25)
Pick's Formula (or Pick's Theorem)
The surface area of a planar lattice polygon is I + ½ B
- 1, where:
- I is the number of lattice points in the polygon's interior.
- B is the number of lattice points on its boundary (vertices & edges).
This result is due to
Georg Pick
(1852-1949) who published it in 1899 ("Geometrisches zur Zahlenlehre"
Sitzungber. Lotos, Naturwissen Zeitschrift Prague,
Volume 19, pages 311-319).
Pick was instrumental in the appointment of Albert Einstein to the German University of Prague
and became a close friend of Einstein's during his stay in Prague, from 1911 to 1913.
Pick's theorem became famous in 1969, when it appeared in the
third edition of the popular book
Mathematical Snapshots which
Hugo
Steinhaus (1887-1972) had first published in 1938...
Lattice points (which Pick called reticular points)
are points whose coordinates are integers. A lattice polygon is
a polygon whose vertices are lattice points.
In the plane, a lattice polygon may be dissected into lattice triangles which
have no lattice points (besides their vertices) inside of them or on their borders.
Therefore, Pick's formula for the area of a lattice polygon is a consequence of the
following (surprising) special case:
A lattice triangle which has no lattice points besides its vertices
(i.e., inside of it,
or on its edges) has a surface area of ½

|
|
 |