Arithmetic & Systems of Numeration
dottcomguy00
(2001-03-21)
Is 1 a prime number?
No, 1 is not prime. This fact turns out to be more than a mere "technicality":
The modern definition of primality is that
"a prime number is a positive integer with exactly two positive divisors".
However, this may seem unconvincing (and/or arbitrary) by itself,
until you stop to consider why we define things the way we do in mathematics,
physics or other sciences.
A relevant quote from Henri Poincaré has been given a superb concise
English translation by John A. Wheeler, namely:
Time is defined so that motion looks simple.
Good mathematical definitions are designed to make theorems simpler to state
and easier to use.
We exclude "1" from the realm of prime numbers
simply because almost all the mathematical discourse about prime numbers,
divisibility and factorizations would be more complex and more difficult if we did not...
Consider just one essential example:
"Every positive number has a unique factorization into primes".
This would not be true if "1" was considered prime since you could add any number of
"1" factors to (other) primes and obtain a product with the same value.
Incidentally, even "1" has a unique factorization into primes,
namely the "empty product" which contains no factors and is therefore equal to 1,
the neutral element for multiplication.
(Why is an empty product equal to one? Why is an empty sum equal to zero?
Well, the same principle applies:
Mathematical discourse would be more complex and crippled with annoying "special cases"
if this was not "defined" to be just so.)
Historically, some number theorists did list "1" as a prime
(e.g., D.N. Lehmer, the father of D.H. Lehmer, in 1914).
A few older textbooks also took this deprecated view, including
(according to Jeff Miller)
Exercices d'analyse numérique [Lebesgue, Paris 1859]
Primary Elements of Algebra for Common Schools and Academies [Joseph Ray, 1866]
and Standard Arithmetic [William J. Milne, 1892].
This goes to show that it's not totally impossible to adopt other definitions.
However, such alternate definitions have proven to be far more awkward to use,
and that's why we got rid of them:
1 is not prime. Period.
On 2004-06-14,
Edgar Bonet
wrote: [edited summary]
Regardless of what's currently accepted for positive integers,
wouldn't it be more natural to call "prime"
anything that does not have a non-trivial factor within a given set?
For example, the invertible polynomials [with real coefficients] are the
nonzero constants (the polynomials of degree zero) which I'd like to call
"prime", along with the polynomials of degree 1
and those polynomials of degree 2 which have no real roots.
|
What you are describing are, in fact, the so-called irreducible
elements of a ring; those which cannot be expressed as a non-trivial product
(a product of two factors being considered trivial if at least one of them
has an inverse in the ring).
The concept of irreducibility is more generally applicable than the concept
of primality, which is restricted to those rings where factorizations
into irreducible elements are essentially unique (which is to say that,
in two such factorizations, every factor of one equals some factor of the other
multiplied by a invertible element of the ring).
One example where factorizations are not unique is the set of
complex numbers
of the form a + ibÖ5,
where a and b are integers.
In this, the number 6 has two unrelated factorizations into irreducible factors:
6 = 2 ´ 3
= (1 + iÖ5)
(1 - iÖ5)
There are only nine discrete "grids" of complex numbers where factorizations
are unique, most notably
Gaussian integers and Eisenstein integers.
In those cases where factorizations can be shown to be unique in the above sense,
the term "prime" is often restricted to those irreducible elements which
are not invertible and have some ad hoc additional feature
which ensures factorization unicity. (We keep as primes only positive numbers
in the case of integers, or polynomials with leading coefficients
equal to 1 in the case of polynomials.)
In this context, invertible elements are commonly called "units".
"Units" and "primes" play totally different roles in this general scheme.
+1 and -1 are units, they are not primes.
(2002-06-16)
Is "composite" the opposite of "prime" ?
No it's not, although it comes close.
Even in the realm of positive integers the number 1 is neither composite
nor prime (see previous article).
The term "irreducible" is favored to
denote something that's not composite, but it's prudent to state exactly
what you have in mind just before you use it for the first time in a speech or a text.
The ugly adjective "noncomposite" could be another option, which does not need
prior explanations...
Anonymous query, via Google (2004-11-05)
What two prime numbers add up to their product?
As each prime divides the sum of both, it must divide the other.
This is only possible if the two primes are equal to some number p.
The sum and the product being both equal to 2p, we must have p = 2.
2 + 2 = 2 ´ 2
(2002-06-14)
Gaussian Integers, Gaussian Primes, etc.
How does the concept of primality generalize beyond ordinary integers?
The so-called Gaussian integers are
complex numbers of the
form a+ib, where a and b are integers.
Gauss showed that each Gaussian integer has a unique factorization
as a product of a so-called "unit" (one of the 4 invertible
elements +1, -1, +i, -i ) and irreducible elements in
an abitrarily chosen "quarter" of the complex plane
(the equivalent of positive primes among ordinary integers).
AlisonWonder
(2002-06-23)
How do you find the lowest common multiple (LCM)
of 3, 7, 24, 86, 125 and 214 ?
Small numbers like these are easily factored into primes:
3 and 7 are prime. 24 is 23´3.
86 is 2´43. 125 is 53.
214 is 2´107.
The factorization of their least common multiple (LCM) is obtained by using for each prime
the highest exponent that appears in each of the above factorizations.
The result is, therefore:
LCM(3,7,24,86,125,214) =
23 ´ 3 ´ 53 ´ 7 ´ 43 ´ 107
= 96621000
Factoring larger numbers into primes is often very difficult,
so it's not a realistic option.
(In fact some modern schemes in public key cryptography do rely on the fact
that it's difficult to retrieve two large prime numbers from their product.)
To find the least common multiple (LCM) of two large numbers,
it's much better to first compute their greatest common divisor (GCD)
using Euclid's algorithm
(or related algorithms that are similarly efficient).
You may then use the relation:
LCM(a,b) = ( a ´ b ) / GCD(a,b)
Given huge numbers like:
a = 2562047788015215500854906332309589561
b = 6795454494268282920431565661684282819
The above formula allows you to "easily" compute the LCM of a and b:
15669251240038298262232125175172002594731206081193527869
Note:
The above numbers (a and b) are not random ones.
They are both products of two very special 19-digit prime numbers...
HINT: Their GCD is 1111111111111111111 and the other factors are of a similar nature
(in nondecimal bases of numeration).
(2002-05-22)
[Anonymous query collected by Site's search engine.]
If you multiply together all the odd numbers from 1 to 999,
what will be the final digit? and why?
-
The answer is 5, because the product of a decimal number ending in 5
and any odd number is a number ending in 5.
Your 500-factor product ends with a 5.
As this example is too simple, let's examine a slightly less trivial one:
-
What's the final digit of the product of
all the odd numbers not divisible by 5 from 1 to 999?
-
This is an example of what's called modular arithmetic:
The remainder in the division by some fixed modulus of a sum, a difference
or a product depends only on the similar remainders for both operands.
Here, the modulus is 10 and each remainder is simply equal to
the last decimal digit of the number involved.
So, the product of 4 decimal numbers ending with 1, 3, 7, and 9,
is a number ending with 9.
If you multiply together an even number of such products, the result ends in 1
(because if you multiply two such products, the result ends in 1,
the same trailing digit as for the ordinary product of 9 and 9, which is 81).
As our product of 400 factors is, in fact, obtained as the product of 100 such
4-tuples, its final digit is thus 1 as well.
-
How do I find the last [least significant] digits of such huge numbers?
-
Modular arithmetic is, again, the key to this question:
If you want the last 5 digits of a product,
use modular arithmetic modulo 100000.
A regular pocket calculator with 10-digit accuracy will give an exact result for the
product of any pair of two 5-digit numbers, which is what any integer reduces to
modulo 100000...
This is all you need to find the last 5 digits of the above products
of 500 or 400 factors...
With less modest means [a precision of several hundred digits], we found that...
- The above product of 500 factors ends with:
...821809277089697420848324327380396425724029541015625.
- The above product of 400 factors ends with:
...251632034302682442928182392469846896720096892926001.
-
What about the leading digits? [most significant digits]
If you want a few leading digits, as well as the number of digits in the result,
the easiest way is to compute the decimal logarithm of such a huge product as the
sum of the decimal logarithms of its factors.
For the 500-factor product, we find a decimal logarithm of 1283.0032378550076961...,
corresponding to a 1284-digit number starting with
100748329763750854004...
For the 400-factor product, we find a decimal logarithm of
1026.28235200247947115...,
corresponding to a 1027-digit number starting with
1915808088370632042699972791343618517...
We may summarize both of the above approaches for either product thusly:
500-factor product of 1284 digits: 10074832976375... ...724029541015625.
400-factor product of 1027 digits: 19158080883706... ...720096892926001.
Iggy
(2004-03-31; email)
What two integers without zero digits
have a product of 1000 000 000 ?
Answer:
512 ´ 1953125 = 1000000000.
The first number is the ninth power of 2, the second is the ninth power of 5.
This pair is the only [positive] solution,
because neither factor could have both a 2 and a 5
in its prime factorization, or else it would be a multiple of 10 and would
thus have a 0 as its last digit, which is ruled out.
Generalization :
We may wonder what powers of 10 are products of two integers without any zero digits.
For large numbers, this is very unlikely because there will normally
be 10% of zeroes among many random digits...
In fact, there seems to be only 11 possibilities,
of which the above is the third largest. Namely:
10 0 = 1 x 1
10 1 = 2 x 5
10 2 = 4 x 25
10 3 = 8 x 125
10 4 = 16 x 625
10 5 = 32 x 3125
10 6 = 64 x 15625
10 7 = 128 x 78125
10 9 = 512 x 1953125
10 18 = 262144 x 3814697265625
10 33 = 8589934592 x 116415321826934814453125
The probability is roughly (0.9)n that
the nth power of 10 would yield a solution.
So, the expected number of solutions above the nth power of 10 is
someting like 10 (0.9)n.
Since we've actually checked that there's no other solution below n = 1500,
we can be very confident that we've not missed anything...
(Peter of Portland, OR.
2000-10-10)
What is the divisibility rule of 13?
(D. S. of Hurricane, WV.
2000-11-29)
What is the divisibility rule for 7?
Recall that a number is divisible by 3 or 9 iff (if and only if) the sum of its digits is.
It is divisible by 11 iff the difference between the sum of its odd digits (units, hundreds,
etc.) and the sum of its even digits (tens, thousands, etc.) is so divisible.
The "quick tests" of divisibility by 7 or 13 are somewhat more complex.
Strangely enough, these two are very strongly related (see below for an explanation).
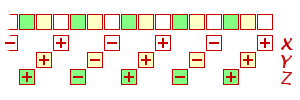The basic process is to form an alternating sum of digits using only every third digit:
From the rightmost digit (the units), you subtract the 4th
rightmost (the thousands),
add the 7th, subtract the 10th, add the 13th, etc.
This gives you the first of three numbers, call this result X.
Do the exact same thing starting with the second rightmost digit (the tens),
subtract the 5th, add the 8th, subtract the 11th, etc.
This gives you a second number, say Y.
Finally, you start with the 3rd rightmost (the hundreds),
subtract the 6th,
add the 9th, subtract the 12th, add the 15th, etc.
This gives you a third number, say Z.
Now, compute the quantity X+10Y+9Z (which is easy to obtain as
X-Z+10(Y+Z), with just three additions and one trivial multiplication by 10).
The original number is divisible by 13 iff this quantity is divisible by 13.
The original number is divisible by 7 iff this quantity is divisible by 7.
It is quite remarkable that the same test works for both 7 and 13!
The real reason why this is so is that
7´13=91=100-10+1.
We are really dealing with divisibility by 91 here!
To see more clearly what happens, consider some base of numeration B,
which may or may not be equal to ten, and consider arithmetic modulo M=B2-B+1
(the expression "X mod M" denotes the remainder when X is divided by M):
(1 mod M) is 1, (B mod M) is B, (B2 mod M) is B-1 (B3 mod M) is M-1
(which is really "-1", that's the ticket!),
(B4 mod M) is M-B, (B5 mod M) is M-(B-1) and
(B6 mod M) is 1,
after which the sequence repeats with period 6.
Therefore, using for base B the alternating sums X,Y and Z defined above for base ten,
we see that the quantity X+BY+(B-1)Z is within a multiple of M of the number
whose divisibility by M is being checked. QED.
In the octal system, for example, the same divisibility test
(based on the quantity X+8Y+7Z) works for 3 and 19.
Just because 3 times 19 is 57=82-8+1.
vorobya
(Alexey Vorobyov.
2002-10-18)
Aurifeuillian Factorization
Prove that n4 + 4 is composite (i.e., not prime) for all n
> 1
Well,
n4 + 4 = (n2 - 2n + 2) (n2 + 2n + 2)
is a proper factorization,
since the first factor is the smaller one and is greater than 1 when
n > 1.
This type of factorization is sometimes called
Aurifeuillian
(less commonly spelled Aurifeuillean) after the Frenchman
[Léon François] Antoine Aurifeuille,
who published a special case in 1873.
Here are some algebraic factorizations:
|
a2 - b2
| = |
( a - b ) ( a + b )
| |
a3 - b3
| = |
( a - b )
( a2 + ab + b2 )
| |
4 a4 + b4
| = |
( 2 a2 - 2ab + b2 )
( 2 a2 + 2ab + b2 )
| |
a6 + b6
| = |
( a2 + b2 )
( a4 -
a2 b2 + b4 )
|
Otisbink
(2002-04-02)
How can I find integer solutions of a linear equation?
For example, (1,4) is an integer solution of 3x + 2y = 11.
How about a harder one like 1024 x - 15625 y = 8404 ?
An equation whose unknown variables are required to be integers is called a
Diophantine equation.
To solve for x and y the linear Diophantine equation
ax + by = c, proceed like this:
First, compute the Greatest Common Divisor (GCD) d of a and b,
using Euclid's Algorithm.
In the process, you will obtain two integers u and v
such that au + bv = d, as explained below.
(The existence of two such integers is a result commonly known as
Bezout's theorem.)
We have a = da' and
b = db' , where a' and b'
are relatively
prime.
Since the RHS of the equation is divisible by d, the LHS must be also.
Therefore, d must divide c, or else the equation has no integer solutions.
Let's assume, then, than c is equal to dc'.
Using the above expression for d, the original equation [divided by d]
may be rewritten as follows:
a' x + b' y = (a' u + b' v) c'
or
a' (x-uc') + b' (y-vc') = 0
Therefore, b' divides the product a' (x-uc').
Since b' and a' are coprime, b' must therefore divide
(x-uc').
In other words, there exists an integer k such that
x = u c' + k b'
and we see that the equation is indeed satisfied if
y = v c' - k a'.
(John of Middletown, NJ.
2000-10-14)
Prove the following:
Given any positive integer N>0, there exists a positive integer M>0 such that MN (M times N)
equals a number whose digits are composed only of 7's and 0's.
Consider the length P of the decimal period of the number 9N
(that is, when computing the decimal expansion of 1/(9N),
the digits ultimately repeat with period P).
We have a relation of the form: 1/9N=K/999...99000..00.
The number 9N thus divides the number which consists of P nines
followed by a certain number J of zeroes.
Therefore, N divides the number consisting of P ones followed by J zeroes,
which is itself a divisor of the integer composed of P sevens followed by J zeroes.
In other words, there is an integer M (M=7K with the above notations)
such that MN is a integer composed of a certain number of 7's
followed by a certain number of zeroes.
(Joe of Ann Arbor, MI.
2000-10-24)
What numbers have exactly 6 proper divisors?
A proper divisor is a number that divides evenly into the dividend,
but is less than (and not equal to) the dividend.
I need to know for a computer homework
if there are any numbers with exactly 6 proper divisors,
because my program keeps running without finding any! [...]
Yes, there are plenty of integers with 6 proper divisors (whether you include "1" as
a "proper" divisor or not):
Consider the factorization into primes of the number
N = AaBbCc...
When it comes to counting the number of divisors
(for the time being let's count both 1 and N as divisors),
only the sequence of exponents a,b,c,... matters
(not the sequence of prime factors A,B,C,...).
To get a divisor of N you should pick one exponent for the first prime among the
(a+1) integers from 0 to a, one exponent for the second prime among the (b+1)
integers between 0 and b, etc.
In other words, the total number of positive divisors
(including 1 and N) is (a+1)(b+1)(c+1)...
If you want the number N to have exactly 6 divisors (counting 1 but excluding itself)
the product (a+1)(b+1)... should be equal to 7.
As 7 is prime this means the product in question only has one factor,
so that you must have a=6 and nothing else.
The number in question must be the sixth power of a prime.
The first of these are 64, 729, 15625, 117649, 1771561, 4826809, etc.
It is worth pointing out that the term "proper divisor" may exclude 1 as well as N.
If you use this convention, the product (a+1)(b+1)... should be equal to 8.
This corresponds to only 3 possible alternatives:
- N is the product of 3 distinct primes.
- N is the product of a prime by the cube of another prime.
- N is the seventh power of a prime.
There are a lot more solutions this time:
- The first class of solutions starts with
2´3´5 = 30, 2´3´7= 42, 2´3´11=66,
2´5´7=70, 2´3´13=78, 2´3´17=102, 3´5´7=105,
2´5´11=110, 2´3´19=114, 2´3´23=138, etc.
- The second class starts with 23´3=24,
23´5=40, 2´33=54, 23´7=56,
23´11=88, 23´13=104, 33´5=135,
23´17=136, etc.
- The third class is the sequence of seventh powers of primes:
128, 2187, 78125, 823543, etc.
The combined list is therefore: 24, 30, 40, 42, 54, 56, 66, 78, 88,
102, 104, 105, 110, 114, 128, 135, 136, 138, ...
Footnote: If you want to exercise your programming talents with a related problem,
you may want to write a program that outputs all the products of 3 distinct primes in
increasing order.
Don't "cheat" at the expense of efficiency (for example, by factoring successive integers
and printing out only those that turn out to be the products of 3 primes).
In fact, you may want the input of your program to be any list of numbers in increasing
order (if it's infinite, like the sequence of primes, such a list is given in terms of
a procedure that generates its successive elements as needed).
The program should then print out in increasing order the products of 3 distinct
elements from the list. To do this efficiently is not as easy as it looks...
(J.E. of Lubbock, TX.
2000-10-25)
Perfect Numbers, Mersenne Primes
A perfect
number is a number whose divisors add up to itself:
1+2+3=6 1+2+4+7+14=28.
After 6 and 28, what are the next perfect numbers?
The proper divisors of a positive integer used to be called
aliquot parts or proper quotients.
These include unity and all other positive divisors of the integer, except itself.
It's often more convenient to consider all the positive divisors of a number.
The sum s(n)
of all the divisors of n
has the desirable property of being multiplicative
(which is to say that
s(pq) = s(p)s(q), whenever p and q are coprime).
A perfect number may thus (also) be defined as an integer n such that
s(n) = 2n.
The factorization into primes of any number n consists of relatively prime factors of the
type pm (p is prime and m is its multiplicity in the factorization);
s(n)/n is the product of the
factors (pm+1-1)/(pm+1-p).
The integer n is a perfect number if and only if this product equals 2.
Only the first four perfect numbers (6, 28, 496 and 8128) were known to Nicomachus
of Gerasa (c.AD 60-120 ; Gerasa is now Jarash, Jordan).
Nicomachus discusses the topic in his celebrated
Arithmetike Eisagoge ("Introduction to Arithmetic", c. AD 100),
an influential work which includes multiplication tables
and the earliest known use of Arabic numerals
(Indian decimal numeration) outside of India.
Nichomachus was the first to deal with Arithmetic independently from geometry,
but his work is far less rigorous than what Euclid had done 4 centuries earlier.
His "results" are often mere guesses.
Wrong guesses tainted the study of
perfect numbers
for centuries...
It's not difficult to show (Euclid did it first) that the even
perfect numbers are the numbers of the form
2n-1(2n-1), provided
(2n-1) is prime.
A prime number of that shape (i.e., one unit less than a power of 2)
is known as a Mersenne prime.
As of March 2005,
only 42 Mersenne primes are known, corresponding to the following values of the
exponent (n):
2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281,
3217, 4253, 4423, 9689, 9941, 11213, 19937, 21701, 23209, 44497, 86243, 110503,
132049, 216091, 756839, 859433, 1257787, 1398269, 2976221, 3021377,
6972593, 13466917, 20996011, 24036583, 25964951, ...
The list is thought to be infinite, but this has yet to be proved.
Double-checking has shown the above list to be complete up to its
38 th member, but
some undiscovered solutions may exist below, or between, the last 4 exponents listed.
The eight
largest known Mersenne primes were found by
GIMPS :
| Rank | Prime Number | Digits | Discovered by | Date |
| 42? | 225964951-1 |
7816230 |
Martin
R. Nowak | 2005-02-18 |
| 41? | 224036583-1 |
7235733 |
Josh Findley | 2004-05-15 |
| 40? | 220996011-1 |
6320430 |
Michael Shafer | 2003-11-17 |
| 39? | 213466917-1 |
4053946 |
Michael Cameron | 2001-11-14 |
| 38 | 26972593-1 |
2098960 |
Nayan Hajratwala | 1999-06-01 |
| 37 | 23021377-1 |
909525 |
Roland Clarkson | 1998-01-27 |
| 36 | 22976221-1 |
895932 |
Gordon Spence | 1997-08-24 |
| 35 | 21398269-1 |
420921 |
Joël Armengaud | 1996-11-13 |
The search for the next Mersenne prime is very active and we encourage you to join it,
by donating your computer's idle time.
This is fully automated and quite painless.
See www.mersenne.org for details
(and/or the latest update).
Therefore, only 42 perfect numbers are known at this [updated] writing,
including huge ones.
Here is the beginning of the list:
6, 28, 496, 8128, 33550336, 8589869056, 137438691328,
2305843008139952128, 2658455991569831744654692615953842176
Of these, the last two (n = 31 and 61 in the above formula)
were respectively discovered by Leonhard Euler (1772) and
I.M. Pervushin (37 digits, in 1883).
The following ones, corresponding to n=89 and n=107,
were discovered by R.E. Powers in 1911 and 1914.
They have respectively 54 and 65 digits.
Before that, the value n=127 had been shown
to give a Mersenne prime of 39 digits (and a perfect number of 77 digits)
by Edouard Lucas (1842-1891) in 1875.
Lucas could only achieve this by designing an efficient test,
which would be the basis of all subsequent efforts,
computerized or not (the "Lucas-Lehmer" test).
Lucas' heroic record would not be broken until the advent of the modern computer.
The next two numbers in the list, the 13th and 14th Mersenne primes,
are much larger (corresponding to n=521 and n=607)
and were both discovered the same day
(January 30, 1952, around 22:00 PST and shortly before midnight)
by Raphael Mitchel Robinson (1911-1995), at the dawn of the computer age.
There's an interesting tale about the later discovery of the 19th and 20th
Mersenne primes (corresponding to exponents 4253 and 4423)
by Hurwitz and Selfridge in 1961:
Because of the way the computer printout was stacked,
Alexander Hurwitz read about the larger number
a few seconds before the smaller one.
The fact that history has now recorded that the 19th Mersenne prime (n = 4253)
never held the record as the
largest known prime
clearly indicates that what we mean by "known" [for now and in this context, at least]
is "known to some human being".
Mathematical and other scientific facts may be gathered automatically,
but they become actual knowledge only when someone is aware of them.
It's simply a question of what our current vocabulary means,
and that meaning may evolve.
Students of philosophy may still have fun wondering if a falling tree makes a sound
when nobody is around to hear it,
but they are currently up against an anthropocentric majority opinion:
In the mid 20th century, we did not [yet?] acknowledge a record broken by a machine,
if nobody was aware of it while it "held"...
Henry Dobb (2002-05-26 e-mail)
was kind enough to confirm the above story, which he heard from John Selfridge
himself around 1990, when Selfridge was a visiting professor of mathematics at
Florida Atlantic University.
Are there any odd perfect numbers?
Nobody knows for sure.
Almost everybody's guess is that there are none, but it's only a guess,
and similar guesses have often been proved wrong in the past...
An
odd perfect number
would necessarily have the following properties:
- No fewer than 300 decimal digits.
[BCR 1991]
- A prime factorization with only one odd exponent.
- At least 8 different prime factors.
[Chein 1979, and/or Hagis 1980]
- At least three prime factors greater than 100.
[Iannucci 2000]
- At least two prime factors greater than 10000.
[Iannucci 1999]
- At least one prime factor greater than 107.
[Jenkins 2003]
- At least one prime power greater than 1020.
[Cohen 1987]
- A sum of the exponents in the prime factorization which has been
shown to be at least 29 by Sayers (1986), at least 37 by
Iannucci
and Sorli (2003) and at least 47 by Kevin
G. Hare (2004,
Update).
An odd perfect number with k prime factors can't exceed
24k
[Nielsen 2003].
The question of finding an odd perfect number, or showing that none exist,
is often presented as the oldest
unsolved mathematical problem...
(S. G.. of San Marcos, TX.
2000-11-22)
How do I represent a floating-point number with hexadecimal normalization?
I can't figure out how to convert exponent and mantissa,
which should both be expressed in binary.
mrjohngribben
(2001-08-10)
How would I write a fractional number in a base other than ten?
What is pi in hexadecimal (base sixteen)?
You can't "convert" mantissa and exponent separately.
Look at the represented number itself and express it in binary.
What you want is probably "binary floating-point"
(it's certainly possible to have "hexadecimal floating-point",
but it's unused in practice).
A binary floating-point number may be written out with hexadecimal digits
for convenience but the exponent still refers to a power of 2 not 16
(again, pure hexadecimal is possible, it's just that we don't use it).
Take p = 3.14159265... for example.
Its first two bits are 1 and 1 (the binary representation of 3),
the next bit is the integral part of twice
0.1415926... namely 0.2831853... so it's 0.
Repeat the process to get each successive bit by doubling the previous fractional part:
You get 0 with 0.56637061...,
1 with 1.3127412...,
0 with 0.265482457... etc.
All told, the (fixed-point) binary representation of p is
pi = 11.0010 0100 0011 1111 0110 1...
You may write this in hexadecimal as 3.243F6... if you wish.
What's the binary floating-point representation of p ?
Well, do just what you would do in decimal:
Shift the pattern so there's just one nonzero digit before the "binary" point
(resist the temptation to call it a "decimal" point)
and record as "exponent" the length of the shift
(that's a negative number if you had to shift the pattern to the left).
For p, you shift the bit pattern only once to the right,
so the exponent is +1 and the pattern is
pi = 1.1001 0010 0001 1111 1011 01... (two)^(+1)
That's the proper binary floating-point representation of p
("two" is spelled out to avoid using multiple bases of numeration in the same expression,
even though "2" would not be ambiguous "16" would be in the discussion that follows).
The commonly used hexadecimal notation is simply a shorthand for the above,
but the exponent still represents a power of two (so the first digit before the
floating point is always a 1 and is therefore actually omitted from many/most/all
internal representations used in computers):
pi = 1.921FA.. (two)^(+1)
What if you wanted everything to use base sixteen? Well, you'd have to shift the bit
pattern by a multiple of 4 only (and count one unit of the exponent for each
"nybble/nibble" of 4 bits so shifted). For p,
this means no shift at all and we have the following purely hexadecimal
representation of p
(I won't repeat it enough, this is not the one used in computers):
pi = 3.243F6... (sixteen)^(0)
What if you have to convert a large decimal floating point number?
Well, you're not gonna like it,
but what you have to do is basically work out the fixed-point representation
and express it in binary (or hexadecimal) using a procedure similar to the above.
For example, instead of attempting to directly "convert" 1.965032919280624e+7,
you would express 19560329.19280624 in binary with the above procedure.
That's tedious, but that's the way it is...
(G. S. of Farley, IA.
2000-11-15)
Can [exponentiation] be calculated, without using a calculator, computer, or the like,
and without actually multiplying the whole thing out
(meaning 1217 = 12x12x12x.....)?
If so, how?
-
Yes, at least two ways:
First way: Use a table of logarithms.
You may use a table of logarithm.
Such tables have been available at your local library
since the early 1600's.
Find the common logarithm of 12 (1.0791812) and multiply by 17.
This gives you 18.3460804.
You then use the log table to find that 0.3460804 is the log of 2.2186,
so that your result is about 2.2186e18.
Second way: Use repeated squaring.
If you want an exact result without going through 17 multiplications,
you can greatly reduce the task by noticing that an even exponent means
squaring the result for an exponent that's only half as big
(so that you "pay" the cost of just one multiplication to halve the exponent
instead of reducing it just by one as you do with the "naive" method).
What if the exponent is odd?
Well, you can reduce the problem to that of an even exponent at the cost of
just one extra multiplication. (Can't you?)
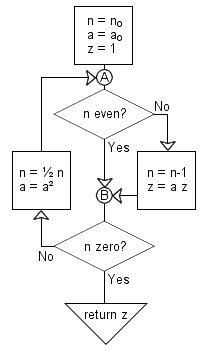
In the case of exponent 17,
you're in luck because you need only one "extra" multiplication:
Squaring 4 times and multiplying once will do the trick:
1217 = (((122)2)2)2
´ 12
In other words:
122 is 144,
1442 is 20736,
207362 is 429981696, finally
42998116962 is 184884258895036416.
Multiply this by 12 to get the answer: 2218611106740436992.
You may think you have not saved yourself a lot of work because you
reduced the number of multiplications only from 16 to 5,
and they were more complicated to perform.
That may be somewhat true in this case.
However, when the exponent is very large, the improved method becomes much better.
Footnote: Number theorists routinely use a computerized version
of the above to compute an
"modulo m" for very large values of the exponent n.
With modular arithmetic, you do not have to deal with larger and larger results
because, at each step, you take the remainder of the division by m, which remains
less than m.
( Steve of Somerville, MA.
2000-11-16)
How many ways can the numbers 1 to 15 be added together to make 15?
Is there a formula for that calculation?
-
The technical term for what you are asking is the "number of partitions of 15",
which is often called p(15).
A partition of n is a collection of positive integers (not necessarily distinct)
whose sum equals n.
This has been studied at length by the best mathematical minds of all times,
including the Indian genius
S.
Ramanujan (1887-1920). He collaborated with
J.H.
Hardy (1877-1947) to come up with a fantastic exact formula for the
partition function p(n), as a sum
[rounded to the nearest integer]
whose number of terms is on the order of Ön.
You may read about this on pages 97-99 of Littlewood's Miscellany by
John
E. Littlewood (1885-1977). In 1937,
Hans Rademacher (1892-1969) gave a formula for p(n) as a convergent series
("On the partition function p(n)" Proc. London Math. Soc. 43 (1937) 241-254).
The number of partitions p(n) is the coefficient of xn in the expansion of
(1+x+x2+x3+...)
(1+x2+x4+x6+...)
(1+x3+x6+...)
(1+x4+x8+...)
(...) ...
This coefficient is indeed obtained by counting the number of ways there is
to choose an exponent multiple of 1 from the
first factor, a multiple of 2 from the second factor, a multiple of 3 from the third, etc.
so these exponents add up to n.
This leads to the formula for the "generating function"
of p(n) which was first given by Euler (1707-1783) as the reciprocal of the products of
all factors (1-xn) where n ranges over the positive integers.
(See Encyclopedia
Britannica.)
Among many other similar essays, we recommend a recent
lecture by Ken Ono.
There are 176 partitions of 15, namely:
15, 14+1, 13+2, 13+1+1, 12+3, 12+2+1, 12+1+1+1, 11+4, 11+3+1, 11+2+2,
11+2+1+1, 11+1+1+1+1, 10+5, 10+4+1, ...
... 2+1+1+1+1+1+1+1+1+1+1+1+1+1+1, 1+1+1+1+1+1+1+1+1+1+1+1+1+1+1.
Values of the Partition Function
[ more... ]
| n |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
8 | 9 | 10 | 11 | 12 | 13 | 14 |
15 | 16 | 17 | 18 | 19 |
|---|
| p(n) |
1 | 1 | 2 | 3 | 5 | 7 | 11 | 15 |
22 | 30 | 42 | 56 | 77 | 101 | 135 |
176 | 231 | 297 | 385 | 490 |
|---|
-
Here's a simple BASIC
program that will compute the number p(n) of partitions of n
as an array of dimension m (m>2). The array "a" is just temporary storage.
The program is based on Euler's basic remark and merely computes the first m
coefficients in the product of all the series
(1+xu+x2u+x3u+ ...).
(arrays "a" and "p" hold the coefficients of the resulting polynomials):
INPUT m
DIM a(m),p(m)
FOR i = 0 TO m: p(i) = 1: NEXT i
FOR u = 2 TO m
FOR i = 0 TO m: a(i) = p(i): p(i) = 0: NEXT i
FOR j = 0 TO m STEP u
FOR k = j TO m
p(k) = p(k) + a(k-j)
NEXT k
NEXT j
NEXT u
REM At this point, p(n) is the number of partitions of n
REM (for any n between 0 and m).
DrGerard (Gérard Michon from Los Angeles, CA.
2000-11-18)
Let M be the sequence: M0= 0, M1= 1, and
Mn+2 = Mn+1 - 2 Mn :
0, 1, 1, -1, -3, -1,
5, 7, -3, -17, -11, 23, 45, -1, -91, -89, 93, 271, ...
A closed expression for Mn is
Mn = (2/Ö7) 2n/2
sin (n atan Ö7 ).
Considering this sequence modulo 8, it's clear that
Mn cannot be equal to 1 if n > 2.
Prove that Mn can't be equal
to -1 if n > 13.
As stated, looking at the sequence modulo 8 (0, 1, 1,
7, 5, 7, 5, 7, ...)
we see it can't go back to +1.
To prove that M never returns to -1 either for
n>13 is more difficult.
We need a few preliminary results about sequences obeying a second-order
linear recurrence relation:
Lemma:
If U0 = 0, U1 = 1, and
Un+2 = A Un+1 + B Un then, for
any sequence V such that Vn+2 = A Vn+1 + B Vn
we have: Vn = V0 Un+1 +
(V1 - A V0 ) Un
(This is easily established by induction on n.)
In particular, with Vn = Un+k+1 :
Un+k+1 = Un+1 Uk+1
+ B Un Uk
For M (namely B = -2) and k = n, we obtain:
M2n+1 = (Mn+1 )2 - 2(Mn )2
Theorem:
Calling x Ù y
the greatest common divisor (GCD) of x and y
(also known as their highest common factor, HCF)
the following relation holds whenever
A Ù B = 1
(that is to say, when the integers A and B are coprime):
Up Ù Uq =
| UpÙq |
Proof (outline):
The case p = q is trivial.
We assume, without loss of generality, that p>q
and we'll let the reader prove, by induction on q, that
Uq+1 Ù Uq = 1.
We then use the above lemma (with n+k+1 = p and k = q):
|
Up Ù Uq |
= |
( Up-q Uq+1 + B Up-q-1 Uq )
Ù Uq =
( Up-q Uq+1 ) Ù Uq |
| = |
Up-q Ù Up |
This parallels the relation
pÙq = (p-q)Ùq ,
on which Euclid's algorithm may be based, and the conclusion follows from
the foundation
U0 = 0.
This theorem shows that a term in the M sequence can only be a prime
or a unit (±1)
if its index is either prime or divisible only by indices corresponding to earlier units
(±1) in the sequence.
Below 13 and besides n = 1, the only such indices are 2, 3, 5, and 13.
We see by inspection that the pairwise products and the squares of these special indices
do not correspond to a -1 value of M.
From this, we deduce that the lowest index n above 13 corresponding to a -1 value
cannot be composite. It must be prime.
Now, consider the sequence modulo 1171.
Its period is 1170, which is divisible by 3, 5 and 13.
The preperiod is of length zero
(which is to say that the two residues 0 and 1 occur again consecutively,
1170 terms later).
Also, the only terms in the first period that are congruent to -1 correspond to
the indices 3, 5 and 13.
This means that any index n for which M is equal to -1 must be of one of the following
three forms (for some integer k):
1170 k + 3,
1170 k + 5, or
1170 k + 13.
Each of these is divisible by 3, 5, or 13.
This implies that n cannot be prime, unless it's equal to 3, 5, or 13...
Therefore, the value -1 occurs only 3 times in the sequence M.
This proof is only convincing if you actually check 1170+2 terms
of the sequence modulo 1171.
There are many moduli like 1171 (including
1991, 3513, 5855, 5973, 6377, 8197, 8971 ...)
for which the period of M is a multiple of
3´5´13
and all the indices of terms congruent to -1 are divisible by 3, 5, or 13...
Before being solved (by the author) on July 8, 2002,
this
problem was one of the first math topics posted (2002-06-08) on the new
AnswerPool.com board,
where it received more attention than 18 months earlier:
- Maiku, have you got the answer to DrGerard's "-1" question yet?
Working on it with a glass of Jack Daniels hasn't helped me one bit.
[Coldfuse, 2002-06-10 on msn
AnswerPoint]
- I fear that the methods required are over my head.
[FlyingHellfish].
- I've given it some thought, but I'm stuck.
[Maiku]
- I got lost really quickly.
[WiteoutKing]
- This one is a doozy!
[Coldfuse,
2002-07-02]
- I have printed [this proof] for posterity [but] what's
the significance of it all?
[Donaldekliros,
2002-07-13] |
In any integer sequence which
(like M) starts with 0 and 1 and obeys a second-order linear recurrence
with coprime coefficients, a prime number can only occur at an index
which is either prime or only divisible by another index where the sequence is
±1.
For example, Mersenne primes
may only occur at prime locations [sic]
in the Mersenne sequence
A000225.
Similarly, Fibonacci primes occur only at prime indices within the
Fibonacci sequence
A000045,
with just one exception (the number 3 occurs at index 4).
The sequence M itself happens to have the lowest [exponential] growth among such
sequences (we're ruling out 6 trivial cases with subexponential growth).
Heuristically, M is thus expected to be more densely populated with primes
than any other sequence ot its kind.
The above result can be used to prove that there are only 9 composite indices
(4, 6, 8, 9, 10, 15, 25, 26, 65) for which M is actually prime.
This makes it much easier to work out the sequence of all the indices n
for which Mn is prime, namely:
4, 6, 7, 8, 9, 10, 11, 15, 17, 19, 23, 25, 26, 29, 31, 47, 53, 65, 67, 71, 73,
113, 127, 199, 257, 349, 421, 433, 449, 691, 761, 823, 991, 1237, 1277, 1399,
1531, 1571, 3461, 3697, 4933, 6199, 7351 ...
(A101087)
Kirk Guidry (2002-03-30; e-mail)
Faulhaber's Formula
[...]
For a given p, how do you derive a formula for the sum of the p-th powers
of the first n integers?
I have seen formulas for up to p = 10,
but I still have difficulties deriving the formula for p = 5...
The general formula you are after is sometimes called Faulhaber's Formula and I'll
give it to you below... However, your question is not really about formulas but
rather about the methods which may be used to obtain them.
I'll give you two such methods.
The first one is elementary and can easily be used to solve your original concern
about the formula for the sum of fifth powers.
The second method is not so elementary
(it involves the concept of generating functions)
but is much more powerful and can be used to establish the general
formula, which involves Bernoulli Numbers.
I still remember fondly the heroic elementary proof I devised for this very formula,
at age 15 or 16, thus "discovering" this mysterious Bernoulli sequence,
which I had never encountered before.
On 2002-12-24, Ben Orin
wrote: [edited text]
[...]
I recall reading a derivation of this formula in my calculus book
(as the trepidation induced by my first encounter with the Bernoulli sequence
serves to vivify).
I remember the dissatisfaction that ensued,
and the prompt contrivance of the formula that would soon pacify me:
To sum the pth powers of the first n integers,
note that this sum is a polynomial in n of degree p+1,
which is thus fully specified by p+2 of its points.
Therefore, for each p, we may express the sum as a
Lagrange interpolating polynomial. For example:
| n | | p+2 |
{ |
k | |
} |
|
| å |
m p = |
å |
å |
m p |
Õ |
(n-j) / (k-j) |
| m=1 | | k=1 | m=1 | |
j Î{1, 2 ... p+2}-{k} |
|
In the above expression, the chosen range for k and j (namely {1, 2, ... p+2})
is an arbitrary example.
As Ben points out, any set of p+2 points would do.
This approach would establish the formula for p=5, say,
by summing up 7 polynomials of degree 6
(each expressed as a product of 6 linear functions of n).
It fails to highlight the relation to the Bernoulli sequence.
Factored expressions for small values of the exponent p.
| p |
|
|---|
| 0 | n+1 |
| 1 | n (n+1) / 2 |
| 2 | n (n+1) (2n+1) / 6 |
| 3 | n2 (n+1)2 / 4 |
| 4 | n (n+1) (2n+1) (3n2+3n-1) / 30 |
| 5 |
n2 (n+1)2 (2n2+2n-1) / 12 |
| 6 |
n (n+1) (2n+1) (3n4+6n3-3n+1) / 42 |
| 7 | n2 (n+1)2
(3n4+6n3-n2-4n+2) / 24 |
| 8 |
n (n+1) (2n+1)
(5n6+15n5+5n4-15n3-n2+9n-3) / 90 |
| 9 | n2 (n+1)2
(2n6+6n5+n4-8n3+n2+6n-3) / 20 |
| 10 |
n (n+1) (2n+1)
(3n8+12n7+8n6-18n5-10n4+24n3+2n2-15n+5) / 66 |
| 11 | n2 (n+1)2
(2n8+8n7+4n6-16n5-5n4+26n3-3n2-20n+10) / 24 |
| 12 |
n (n+1) (2n+1)
(105n10+525n9+525n8-1050n7-1190n6+2310n5
+1420n4-3285n3-287n2+2073n-691) / 2730 |
| 13 |
n2 (n+1)2
(30n10+150n9+125n8-400n7-326n6+1052n5
+367n4-1786n3+202n2+1382n-691) / 420 |
| 14 |
n (n+1) (2n+1)
(3n12+18n11+24n10-45n9-81n8+144n7+182n6-345n5
-217n4+498n3+44n2-315n+105) / 90 |
| 15 |
n2 (n+1)2
(3n12+18n11+21n10-60n9-83n8+226n7+203n6-632n5
-226n4+1084n3-122n2-840n+420) / 48 |
Denominator sequence: 1,2,6,4,30,12,42,24,90,20,66,24,2730,420,90,48...
(2002-11-16) Multiplicative Functions
(and Dirichet Convolution)
An important class of arithmetic functions:
An arithmetic function (or arithmetical function)
is a numeric function (with real or complex values)
of the positive integers.
In the context of number theory,
an arithmetical function f is said to be multiplicative if
f(ab) = f(a) f(b)
whenever the integers a and b are coprime.
If we rule out the function that's identically zero [as is usually done in this context]
this implies that f(1) = 1
for any multiplicative function f.
The zero function must be ruled out as a multiplicative function
to ensure that a unique multiplicative function is specified by values
attributed to the prime powers, as stated next.
Otherwise, there would be one [and only one] ambiguity between the [useless]
zero function and the [very important] Dirichlet unit
(e) defined below.
To define a multiplicative function,
it is sufficient to specify its value when the argument is the
positive power of a prime
( pn ). Here are a few examples:
- Dirichlet unit:
e(pn ) = 0 [e(k) =
ë1/k
û
= 0k-1 is zero unless k=1]
- Unit constant:
u(pn ) = 1 [u(k) = 1, for any positive integer k]
- Identity function:
N(pn ) = pn [N(k) = k, for any k]
- Number of divisors (so ) :
d(pn ) = n+1.
- Sum of the divisors (s1 ) :
s(pn ) =
(pn+1 -1) / (p-1)
- Abundancy:
s-1 (n) =
s(n) / n
[A perfect number has abundancy 2.]
- Other divisor functions:
sk (pn ) =
(pkn+1 -1) /
(pk -1)
sk (n) is the sum of the k-th powers of the
divisors of n.
- Möbius function:
m(p) = -1 and
m(pn ) = 0
for n>1.
- Liouville's function:
l(pn ) = (-1)n
- [Euler's] totient function:
f(pn ) =
pn-1 (p-1)
f(n) is the number of positive integers
less than n and coprime to n.
- GCD-sum function: g(pn ) =
(n+1) pn - n pn-1
[K.A.
Broughan]
g(n) is the sum of the GCD's with n of the first n integers.
[ g = f*N ]
The ordinary product of two multiplicative functions
is itself a multiplicative function
(so is their quotient, assuming a divisor with only nonzero values).
A multiplicative function raised to the power of an integer is also a
multiplicative function
(so is the nonintegral power of a multiplicative function with
positive real values).
Another very interesting operation must be introduced in this context:
Dirichlet Multiplication
( f * g )
& Inversion Formulas
If f is a multiplicative function and F(n) is defined as the
sum of the terms f(d) for all divisors d of n, then F is a multiplicative
function called the sum-function of f.
The function f may be retrieved from F using the so-called
Möbius inversion formula, which states that
f(n) is the sum of all terms
F(d)m(n/d) for all divisors d of n,
where m is the aforementioned Moebius function.
More generally, if f and g are two multiplicative functions,
another multiplicative function F may be defined by letting F(n) be the sum of the
terms f(d) g(n/d) for all divisors d of n.
The function F is the Dirichlet product
( f*g )
of f and g :
| F(n) =
f*g (n) = |
å |
f(d) g(n/d) |
| |
d | n |
|
The Dirichlet product (also called Dirichlet convolution) is an associative
and commutative operation among arithmetic functions.
Its neutral element (e)
is the Dirichlet unit defined above.
Any arithmetic function f for which f(1) is nonzero
has a Dirichlet inverse (this is the case for all multiplicative functions,
since we're ruling out the zero function, as stated above).
If f(1) = 1 and all values of f
are integers, then the same is true for the Dirichlet inverse of f.
The Dirichlet inverse of the unit constant u [u(n) = 1]
is the Möbius function m.
This statement is equivalent to the aforementioned
Möbius inversion formula :
If F = u * f
then f = m * F
Dirichlet Powers :
Dirichlet powers m[k]
of the Möbius function are easily defined (2004-11-27):
m[k] (pn )
= (-1)n C(k,n)
This formula holds even if k is negative
[u = m[-1] or powers of u,
like d = u*u].
More surprisingly, it's also true for fractional values of k...
It's not difficult to show that, for any positive integer q and any arithmetic function
f with real positive f(1) there's a unique
root
(real positive at point 1) of which f is the Dirichlet q-th power.
This defines the Dirichlet 1/q power of f
and the p/q power of f is the p-th power of that thing.
Any such Dirichlet power of a multiplicative function is itself a multiplicative function.
Dirichlet square root of the Möbius function :
m [ ½ ] (pn) =
(-1)n C(½,n)
| m = |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
10 | 11 | 12 |
| m[½] (m) |
1 | -1/2 | -1/2 | -1/8 | -1/2 | 1/4 |
-1/2 | -1/16 | -1/8 | 1/4 | -1/2 | 1/16 |
Other Special Examples :
Here are some relations involving the above standard multiplicative functions,
featuring links to Sloane's
Encyclopedia of Integer Sequences :
Completely Multiplicative Functions :
A function f is called completely multiplicative
(or totally multiplicative) when
f(ab) = f(a) f(b)
always holds (whether a and b are coprime or not)
in which case its Dirichlet inverse g
is easily defined:
g(n) = m(n) f(n),
since:
|
g*f (n) = |
å |
m(d) f(d) f(n/d)
= f(n) |
å |
m(d)
= f(n) e(n)
= e(n) |
| |
d | n |
|
d | n |
|
The last equality holds for n=1 because f(1)=1,
and for n>1 because e(n)=0.
A completely multiplicative function f and its dirichlet
inverse g are entirely determined by whatever
values f(p) are chosen for prime numbers p, since:
f (pn ) =
f (p) n
whereas
g(p) = - f (p)
&
g(pn ) = 0, if n>1
A multiplicative function which is zero for squares of primes, and higher powers of
prime numbers, is thus the Dirichlet inverse of a totally
multiplicative function.
|
