Mathematical Symbols and Scientific Icons
 Emily Guerin (2004-06-18; e-mail)
The Equality Symbol
Who was the first person to use the = (equal) sign?
A very elongated form of the modern equality symbol (=) was first introduced in print
in The Whetstone of Witte (1557) by
Robert
Recorde (1510-1558) the man who first introduced algebra into England.
He justified the symbol by stating
that no two things can be more equal than a pair of parallel lines...
We've been told that a manuscript from the University of Bologna, dated between 1550 and 1568,
features the same equality symbol,
apparently independently of the work of
Robert Recorde (and possibly slightly earlier).
William
Oughtred (1574-1660) was instrumental in the subsequent popularization
of the symbol,
which appears next in 1618, in the appendix [attributed to him]
of the English translation by Edward Wright of John Napier's
Descriptio
(where early logarithms were first described in 1614).
The mathematical symbol is then seen again, and perhaps more importantly,
in Oughtred's masterpiece Clavis Mathematicae (1631) in which other mathematical
symbols are experimented with, which are still with us today
(including ´ for multiplication).
Instead of the now familiar equality symbol,
many mathematicians of that era used words or abbreviations (including "ae" for the
Latin aequalis) well into the 18th century.
Thomas
Harriot (1560-1621) was using a slightly different symbol
( ),
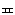while some others used a pair of vertical lines ( || ) instead.
Earliest Uses of Symbols of Relation
(Jeff Miller)
 (2003-08-08)
¥
The infinity symbol introduced by John Wallis in 1655.
This symbol was first given its current mathematical meaning in
"Arithmetica Infinitorum" (1655)
by the British mathematician John Wallis (1616-1703).
+¥ (resp. -¥)
is simply the mathematical symbol used to denote the "limit" of a real quantity which
eventually remains above (resp. below) any preset bound.
Also, in the canonical map between the complex plane
and a sphere minus a point, the
unsigned symbol (¥) corresponds to
the "missing point" of the sphere,
but ¥ is not a
proper complex number... It's just a convenient symbol for the fictitious
"circle at infinity" beyond the horizon of the complex plane, so to speak.
The symbol itself is properly called a lemniscus,
a latin name which means "pendant ribbon"
and was first used in 1694 by Jacob Bernoulli (1654-1705)
to describe a planar curve now called the
Lemniscate of Bernoulli.
The design was a part of Western iconography well before modern times.
In particular, it's found on the cross of
Saint Boniface
(bishop and martyr, English apostle of Germany, né Winfrid c.675-755).
The infinity snake, the
ouroboros symbol
(also, uroboros or uroborus)
is a serpent or a dragon biting its own tail
(ourobóroV
means "tail swallower" in Greek).
The symbol appeared in Egypt as early as 1600 BC, and independently
in Mesoamerica (see a Mayan version at left).
It has been associated with the entire Zodiac and the eternity of time.
It's the symbol of the perpetual cyclic renewal of life.
It has been found in Tibetan rock carvings and elsewhere
depicted in the shape of a lemniscate, although a plain circle is more common
(the circle symbolizes infinity in Zen Buddhism).
The Lemniscate or Infinity Symbol
  (2003-11-10)
Symbols of Infinite Numbers
w and
Ào, the other
infinity symbols.
As discussed above, the infinity symbol of Wallis
(¥) is not a number...
However, there are two different approaches that make sense of actual
infinite numbers. Both of them were first investigated by
Georg
Cantor (1845-1918).
Two sets are said to have the same cardinal number of elements
if they can be put in one-to-one correspondence with each other.
For finite sets, the natural integers (0,1,2,3,4 ...) are
adequate cardinal numbers, but transfinite cardinals
are needed for infinite sets.
The symbol Ào (pronounced
"aleph zero", "aleph null", or "aleph nought") was introduced by Cantor to
denote the smallest of these (the cardinal of the set of the integers themselves).
He knew that more than one transfinite cardinal was needed because his famous
diagonal argument
proves that reals and integers have different cardinality.
The second kind of infinite numbers introduced by Cantor
are called transfinite ordinals.
Observe that a natural integer may be represented by
the set of all nonnegative integers before it,
starting with the empty set ( Æ )
for 0 (zero) because there are no nonnegative integers before it.
So, 1 corresponds to the set {0}, 2 is {0,1}, 3 is {0,1,2}, etc.
For the ordinal corresponding to the set of all the nonnegative integers {0,1,2,3...}
the w infinity symbol was introduced.
Cantor did not stop there, since {0,1,2,3...w}
corresponds to another transfinite ordinal, which is best "called"
w+1.
{0,1,2,3...w,w+1} is w+2, etc.
Thus, w is much more like an ordinary number than
Ào.
In fact, within the context of surreal numbers
described by John H. Conway around 1972, most of the usual rules of arithmetic apply to
expressions involving w (whereas Cantor's scheme for
adding transfinite ordinals is not even commutative).
Note that 1/w is another nonzero
surreal number, an infinitesimal one.
By contrast, adding one element to an infinity of
Ào elements
still yields just Ào
elements, and 1/Ào
is meaningless.
Infinite Ordinals and Transfinite Cardinals
|
The Surreal Numbers of John H. Conway
  (2005-04-10)
Cap: Ç
Cup: È
Wedge: Ù
Vee: Ú
Intersection (greatest below) & Union (lowest above).
The chevron (wedge) and inverted chevron (vee) are the generic symbols used
to denote the basic binary operators induced by some partial ordering.
The chevron symbol (wedge) denotes the highest element "less" than (or equal to)
both operands.
The inverted chevron symbol (vee) denotes the lowest element "greater" than
(or equal to) both operands.
Among positive integers, consider the relation (usually denoted by a vertical bar)
which we may call "divides" or "is a divisor of". It is indeed
an ordering relation, because it's reflexive, antisymmetric
and transitive.
It's only a partial ordering relation because, for example,
2 and 3 can't be "compared" to each other (as neither divides the other).
pÙq is the greatest common divisor
(GCD) of p and q, more rarely called their highest common factor (HCF).
Conversely, pÚq is their
lowest common multiple (LCM).
| pÙq = gcd(p,q)
[ = (p,q) ] (*) |
| pÚq = lcm(p,q) |
(*) We do not recommend the widespread but dubious notation (p,q)
for the GCD of p and q. It's unfortunately dominant in English texts.
In the context of Number Theory, the above use of the "wedge" and "vee" mathematical
symbols needs little or no introduction, except to avoid confusion with the meaning
they have in predicate calculus (the chevron symbol stands for "logical and", whereas
the inverted chevron is "logical or", also called "and/or").
In Set Theory, the fundamental ordering relation among sets may be
called "is included in" (Ì or, more precisely,
Í).
In this case, and in this case only,
the corresponding symbols for the related binary operators assume
rounded shapes and cute names:
cap (Ç) and
cup (È).
AÇB and AÈB
are respectively called the intersection and the union of the sets A and B.
The intersection AÇB is the set of all elements that
belong to both A and B.
The union AÈB is the set of all elements that
belong to A and/or B ("and/or" means "either or both";
it is the explicitly inclusive
version of the more ambiguous "or" conjunction, which normally does mean "and/or"
in any mathematical context).
The chevron symbol is also used for the exterior product
(the wedge product).
In an international context, the same mathematical symbol may be found to denote
the vectorial cross product
as well...
(2005-09-26)
"Blackboard Bold" or Doublestruck Symbols
Letters enhanced with double lines are symbols for sets
of numbers.
Such symbols are attributed to Nicolas Bourbaki,
although they don't appear in the printed work of Bourbaki... Some
Bourbakists like Jean-Pierre Serre advise against
them, except in handwriting (including traditional blackboard use).
Some
Doublestruck Symbols and their Meanings| Doublestruck | Bold |
Etymology | Symbol's Meaning |
|---|
 | P | Prime
Numbers | 2, 3, 5, 7, 11, 13, 17... |
 | N | Natural
Numbers | Monoid of Natural Integers |
 | Z | Zahl
[German] | Group of Integers |
 | Q |
Quotient | Field of Rational Numbers |
 | R |
Real | Field of Real Numbers |
 | C |
Complex | Field of Complex Numbers |
 | H |
Hamilton | Skew Field of Quaternions |
ln(x) =
|
ó x
õ1 |
dt |
 |
| t |
(2003-08-03)
ò
The integration symbol introduced by Leibniz.
Gottfried Wilhelm Leibniz
thought of integration as a generalized summation,
and he was partial to the name "calculus summatorius"
for what we now call [integral] calculus.
He eventually settled on the familiar elongated "s" for the sign of integration,
after discussing the matter with Johann Bernoulli,
who favored the name "calculus integralis"
and the symbol I for integrals...
Eventually, what prevailed was the symbol of Leibniz, with the name advocated by Bernoulli...
(2002-07-05)
Q.E.D.
[ QED =
Quod Erat Demonstrandum ]
What's the name of the end-of-proof box, in a mathematical context?
Mathematicians call it a halmos symbol, after
Paul
R. Halmos (1916-) who is also credited with
the "iff" abbreviation for "if and only if".
Typographers call it a tombstone, which is the name of the symbol in any
non-scientific context.
Before Halmos had the idea to use the symbol in a mathematical context,
it was widely used to mark
the end of an article in popular magazines (it still is).
Such a tombstone is especially useful for an article which
spans a number of columns on several pages,
because the end of the article may not otherwise be so obvious...
Some publications use a small stylized logo in lieu of a plain tombstone symbol.
See Math Words...
Here's a halmos symbol, at the end of this last line!
Jacob Krauze
(2003-04-20; e-mail)
As a math major, I had been taught that the symbol ¶
(used for partial derivatives) was pronounced "dee",
but a chemistry professor told me it was actually pronounced "del".
Which is it?
I thought "del" was reserved for [Hamilton's nabla operator]
Ñ = < ¶/¶x,
¶/¶y,
¶/¶z > ...
"Del" is indeed a correct name for both
¶ and Ñ.
Some authors present these two as the lowercase and uppercase versions of the same
mathematical symbol, although the terms
"small del" and "big del" [sic!] are rarely used, if ever...
Physicists and others often pronounce
¶y/¶x
"del y by del x".
In an international scientific context, the possible confusion between
¶ and Ñ
is probably best avoided by calling the
Ñ mathematical symbol "nabla del",
or simply nabla.
William Robertson Smith (1846-1894) coined the name "nabla"
for the Ñ
mathematical symbol, whose shape is reminiscent
of a Hebrew harp by the same name (also spelled "nebel").
The term was first adopted by Peter Guthrie Tait (1831-1901)
by Hamilton and also by Heaviside.
Maxwell
apparently never used the name in a scientific context.
The question is moot for many mathematicians, who routinely read
a ¶ symbol
like a "d" (mentally or aloud).
I'm guilty of this myself, but don't tell anybody!
When it's necessary to lift all ambiguities without sounding overly pedantic,
"¶" is also routinely called
"curly d", "rounded d" or "curved d".
It corresponds to the cursive "dey" of the Cyrillic alphabet and is sometimes
also known as Jacobi's delta, because Carl Gustav Jacobi is credited with
the popularization of the symbol's modern mathematical meaning
(starting with the 1841 publication of his epoch-making paper entitled
"De determinantibus functionalibus",
in which what we now call Jacobians
are presented.).
Historically, this mathematical symbol was first used by Condorcet in 1770,
and by Legendre around 1786.
 (2003-06-10)
Borromean Links
What are Borromean rings?
These are 3 interwoven rings which are pairwise separated (see picture).
Interestingly,
it can be shown that such rings cannot all be perfect circles
(you'd have to bend or stretch at least one of them)
and the converse seems to be true:
three simple unknotted closed curves may always be placed
in a Borromean configuration unless they are all circles
[no other counterexamples are known].
The design was once the symbol of the alliance between
the Visconti, Sforza and Borromeo families.
It's been named after the Borromeo family who has perused the three-circle symbol,
with several
other interlacing patterns!
The three rings are found among the many symbols featured on the
Borromeo
coat of arms (they are not nearly as prominent as one would expect,
you may need a closer look).
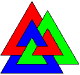
The Borromean interlacing is also featured in other symbols which do not involve rings.
One example, pictured at left, is [one of the two versions of] the so-called
Odin's triangle.
In a recent issue of the journal Science
(May 28, 2004)
a group of chemists at UCLA reported
the synthesis of a molecule with the Borromean topology.
 (2003-06-23)
The tai-chi mandala: Taiji or Yin-Yang symbol.
Niels Bohr's coat-of-arms: "Argent, a taiji Gules and Azure."
The Chinese Taiji symbol (Tai-Chi, or taijitu)
predates the Song dynasty (960–1279). Known in the West as the
Yin-Yang symbol,
it appears in the ancient I Ching (or YiJing,
the "Book of Changes").
It is meant to depict the two traditional types of complementary principles
from which all things are supposed to come from, Yin and Yang,
whirling within an eternally turning circle representing the primordial void
(the Tao).
The Confucian Tai-Chi symbol represents actual plenitude,
whereas the Taoist Wu-Chi symbol (an empty circle) symbolizes undifferentiated emptiness,
but also the infinite potential of the primordial Tao...
 Yin and Yang are each divided into greater and lesser "phases"
(or "elements"). A fifth central phase (earth)
represents a perfect transformation equilibrium.
To a Western scientific mind, this traditional Chinese classification may seem entirely
arbitrary, especially the more recent "scientific" extensions to physics and chemistry,
which are highlighted in
the following table:
| Yin | Yang |
|---|
| Etymology | Dark Side (French: ubac) | Bright
Side (French: adret) |
| Gender | Female, Feminine | Male, Masculine |
| Celestial | Moon, Planet, Night | Sun, Star, Day |
| Ancient Symbol | White Tiger | Green Dragon |
| Colors | Violet, Indigo, Blue | Red, Orange, Yellow |
Greater Phase
Equinox
Transition, Young | West, Metal
and Autumn
Potential Structure | East, Wood
and Spring
Potential Action |
| Weak Nuclear Force | Gravity |
Lesser Phase
Solstice
Stability, Old | North, Water
and Winter
Actual Structure | South, Fire
and Summer
Actual Action |
| Strong Nuclear Force | Electromagnetism |
General
Features |
Dark, Cold, Wet
Solid, Heavy, Slow
Curling, Deep
Soft voice,
Sad
Yielding, Soft,
Relaxed
Stillness, Passivity
Coming, Inward, Pull
Receive,
Grasp, Listen
Descending,
Low, Bottom
Contracting, Preserving
Small, Interior, Bone
Mental, Subtle
Buy |
Bright, Hot, Dry
Gas, Light, Fast
Stretching, Shallow
Loud voice,
Happy
Resistant, Hard,
Tense
Motion, Activity
Going, Outward, Push
Transmit,
Release, Talk
Ascending,
High, Top
Expanding, Consuming
Large, Exterior, Skin
Physical, Obvious
Sell |
| Food | Sweet, Bitter, Mild
Vegetable, Root
Red meat |
Salty, Sour, Hot
Fruit, Leaf
Seafood |
Geometry
Topology | Space, Open angle
Finite, Discontinuous |
Time, Closed circle
Infinite, Continuous |
| Logic | Cause | Effect |
| Orientation | Dexter, Negative, Loss
Front, Counterclockwise | Sinister,
Positive, Gain
Back, Clockwise |
| Binary
Arithmetic | 0, Zero, Even, No
 | 1, One, Odd, Yes
 |
| Chemistry | Acidic, Cation, Oxidant | Alkaline,
Anion, Reductant |
| Genetic
Code | Pyrimidines: Cytosine, Thymine | Purines:
Guanine, Adenine |
| Particle Physics |
Matter, Particle, Fermion |
Energy, Force, Boson |
| Yin | Yang |
|---|
The traditional Chinese taiji symbol became a scientific icon
when Niels Bohr made it his coat-of-arms in 1947
(with the motto: contraria sunt complementa)
but the symbol was never meant to convey any precise scientific meaning...
The oldest known Tai-Chi symbol
was carved in the stone of a Korean Buddhist temple in AD 682.
A stylized version of the Ying-Yang symbol
(Eum-Yang to Koreans) appears on the modern [South] Korean Flag
(T'aeGuk-Ki)
which was first used in 1882, by the diplomat Young-Hyo Park on a mission to Japan.
The flag was banned during the Japanese occupation of Korea, from 1910 to 1945.
|
) denotes the
quantum of spin.
![Modern [South] Korean Flag](taeguk.gif)
