• Primary conversion factors  between customary systems of units.
  6 Basic Dimensionful Physical Constants  (Proleptic SI)
• Speed of Light in a Vacuum (Einstein's Constant):   c = 299792458 m/s.
• Magnetic Permeability of the Vacuum: An exact value defining the ampere unit.
• Planck's constant:  The ratio of a photon's energy to its frequency.
• Boltzmann's constant:  Relating temperature to energy.
• Avogadro's number:  The number of things per mole of stuff.
• Mechanical Equivalent of Light (683 lm/W at 540 THz) defines the candela.
  Fundamental Mathematical Constants: 
• 0:  Zero is the most fundamental and most misunderstood of all numbers.
• 1 and -1:  The unit numbers.
• p ("Pi"): The ratio of the circumference of a circle to its diameter.
• Ö2: The diagonal of a square of unit side.  Pythagoras' Constant.
• f: The diagonal of a regular pentagon of unit side.  The Golden Number.
• Euler's  e:  The base of the exponential function which equals its own derivative.
• ln(2):  The alternating sum of the reciprocals of the integers.
• Euler-Mascheroni Constant  g :  The limit of   [1 + 1/2 + 1/3 +...+ 1/n] - ln(n).
• Catalan's Constant  G :  The alternating sum of the reciprocal odd squares.
• Apéry's Constant  z(3) :  The sum of the reciprocals of the perfect cubes.
• Imaginary  i:  If "+1" is a step forward, then "+ i" is a step sideways to the left.
  Exotic Mathematical Constants: 
• Mertens constant:  How the sum of reciprocal primes (< n) differs from ln(ln n).
• Ramanujan-Soldner constant (m):  The positive root of the logarithmic integral.
• The Omega constant:  W(1) is the solution of the equation   x exp(x) = 1.
• Feigenbaum constant (d) and the related reduction parameter (a).
  Third Tier Mathematical Constants: 
• Brun's Constant:  Stated standard uncertainty  (s)  means a 99% level of  ±3s
• Prévost's Constant:  The sum of the reciprocals of the Fibonacci numbers.
• Grossman's Constant:  The initial point which makes some recurrence converge.
• Ramanujan's Number:   exp(p Ö163)   is almost an integer.
• Viswanath's constant is the mean growth in random additions and subtractions.

Related articles on this site:

• Anything raised to the power of 0 is equal to 1, including 0 to the power of 0.
• Using the Golden Ratio (f) to express the 5 [complex] fifth roots of unity.
• Wilbraham-Gibbs constant and 9% overshoot of partial Fourier series at a jump.
• What is a continued fraction?  Example:  The expansion of p.
• Regular patterns in the continued fractions of some irrational numbers.
• Physical Units: A tribute to the late physicist Richard P. Feynman (Nobel 1965).
• Mathematical Symbols and Scientific Icons
• Perimeter of an Ellipse.  Surface Area of an Ellipsoid.
• Scientific Icons and Symbols.

---

(2003-07-26)     0
Zero is a number like any other, only more so...

Zero is probably the most misunderstood number.  Even the imaginary number i is probably better understood, (because it's usually introduced only to comparatively sophisticated audiences).  It took humanity thousands of years to realize what a great mathematical simplification it was to have an ordinary number used to indicate "nothing", the absence of anything to count...  It's only with the introduction of zero that the ancient Indian system of numeration could take off and become the familiar decimal system we use today.

The counting numbers start with 1, but the natural integers start with 0...  Most mathematicians prefer to start with zero the indexing of the terms in a sequence, if at all possible.  Physicists do that too, in order to mark the origin of a continous quantity:  If you want to measure 10 periods of a pendulum, say "0" when you see it cross a given point from left to right (say) and start your stopwatch.  Keep counting each time the same event happens again and stop your timepiece when you reach "10", for this will mark the passing of 10 full periods.  If you don't want to use zero in that context, just say something like "Umpf" when you first press your stopwatch; many do...  

A universal tradition, which probably predates the introduction of zero by a few millenia, is to use counting numbers (1,2,3,4...) to name successive intervals of time; a newborn baby is "in its first year", whereas a 24-year old is in his 25th.  When translated to calendars this unambiguous tradition seems to disturb more people than it should.  Since the years of the first century are numbered 1 to 100, the second century goes from 101 to 200, and the twentieth century consists of the years 1901 to 2000.  The third millenium starts with January 1, 2001.

For some obscure reason, many people seem to have a mental block about some ordinary mathematical statements when they apply to zero.  A number of journalists, who should have known better, once questioned the simple fact that zero is even.  Of course it is:  Zero certainly qualifies as a multiple of two (it's zero times two).  Also, in the integer sequence, any even number is surrounded by two odd ones, just like zero is surrounded by the odd integers -1 and +1...  Nevertheless, we keep hearing things like:  "Zero, should be an exception, an integer that's neither even nor odd."  Well, why on Earth would anyone want to introduce such unnatural exceptions where none is needed?

What about 0⁰ ?  Well, anything raised to the power of zero is equal to unity and a closer examination would reveal that there's no need to make an exception for zero in this case either:  Zero to the power of zero is equal to one!  Any other "convention" would invalidate a substantial portion of the mathematical literature (especially concerning common notations for polynomials and/or power series).

A related discussion involves the factorial of zero (0!) which is also equal to 1.  However, most people seem less reluctant to accept this one, because of the generalization of the factorial function (involving the Gamma function) which happens to be continous about the origin...

---

(2003-07-26)     1
The unit number to which all nonzero numbers refer.

---

(2003-07-26)     p = 3.141592653589793238462643383279502884197+
The ratio of the circumference of a circle to its diameter.

 

It can be of no practical use to know that Pi is irrational, but
if we can know, it surely would be intolerable not to know.
Edward Charles Titchmarsh (1899-1963)

The symbol "p" for the most famous transcendental number was introduced in a 1706 textbook by William Jones (1675-1749), reportedly because it's the first letter of the Greek verb perimetron ("to measure around") from which the word "perimeter" is derived.  Euler popularized the notation after 1736.  It's not clear whether Euler knew of the previous usage pioneered by Jones.

Expansion of Pi as a Continued Fraction   |   Mnemonics for pi

---

(2003-07-26)     Ö2 = 1.41421356237309504880168872420969807857-
The diagonal of a square of unit side.  Pythagoras' Constant.

 

He is unworthy of the name of man who is ignorant of the fact
that the diagonal of a square is incommensurable with its side.
Plato (427-347 BC)

---

(2003-07-26)     f = 1.618033988749894848204586834365638117720+
The diagonal of a regular pentagon of unit side:  f =  (1+Ö5) / 2

f² = 1 + f.  This ubiquitous number is also known as the Golden Number or the Golden Section; it's the aspect ratio of a rectangle whose semiperimeter is to the larger side what the larger side is to the smaller one.

The 5 Fifth Roots of Unity   |   Continued Fraction   |   Wythoff 's Game

---

(2003-07-26)     e = 2.718281828459045235360287471352662497757+
The base of an exponential function equal to its own derivative:  å 1/n!

Among many other things, e is also the limit of   (1 + ¹/_n ) ⁿ  as n tends to infinity.

The letter e may now no longer be used to denote
anything other than this positive universal constant.
Edmund Landau (1877-1938) 

The Invention of Logarithms   |   Mnemonics for e

---

(2003-07-26)     ln(2) = 0.6931471805599453094172321214581765681-
The alternating sum   1 - 1/2 + 1/3 - 1/4 + 1/5 - 1/6 + 1/7 - 1/8 + ...
or the "straight" sum   ½ + (½)²/2 + (½)³/3 + (½)⁴/4 + (½)⁵/5 + ...

The first few decimals of this pervasive constant are worth memorizing!

---

(2003-07-26)     g = 0.577215664901532860606512090082402431042+
The limit of   [1 + 1/2 + 1/3 + 1/4 + ... + 1/n] - ln(n) ,   as n ® ¥

The Euler-Mascheroni constant is named after Leonhard Euler (1707-1783) and Lorenzo Mascheroni (1750-1800).  It's also known as Euler's constant.

This number was first denoted "g" by Euler, who calculated it to 16 digits in 1781.  In 1790, Mascheroni gave 32 digits, but only the first 19 of these were correct, because of a mistake which was corrected only in 1809, by Johann von Soldner.  In 1878, Adams worked out the thing to 260 decimal places.  It was computed to 7000 digits in 1974 (W.A. Beyer and M.S. Waterman) and to 20 000 digits in 1980 (R.P. Brent).  Over 100 000 000 digits are now known...

Everybody's guess is that g is transcendental but this constant has not even been proven irrational yet...

Charles de la Vallée-Poussin (1866-1962) is best known for having given an independent proof of the Prime Number Theorem in 1896, at the same time as Jacques Hadamard (1865-1963).  In 1898, de la Vallée-Poussin considered the average fraction by which the quotient of a positive integer n by a lesser prime falls short of an integer.  He proved that this quantity tends to  g  for large values of n (and not to ½, as might have been naively expected).

---

(2003-07-26)     G = 0.915965594177219015054603514932384110774+
Catalan's Constant, alternating sum of the reciprocal odd squares.  b(2)

Dirichlet Beta Function (b)

---

(2003-07-26)     z(3) = 1.2020569031595942853997381615114499908-
Apéry's Constant, the sum of the reciprocal cubes:   å 1/n ³

 

Apéry's incredible proof appears to be a mixture of miracles and mysteries.
Alfred van der Poorten

What caused van der Poorten's admiration is the 1977 proof by the French mathematician Roger Apéry (1916-1994) of the irrationality of z(3), starting with the remarkable expression below (featuring a series that converges quickly):

z(3)		5		¥ å k=1		(-1) k-1
		2				k3  ì î 2k k ü þ

Average Energy of a Thermal Photon   |   Experimental Mathematics and Integer Relations

---

(2003-07-26)     i, the basic imaginary number.
If  +1 is one step forward, i is a step sideways to the left...

Idiot's Guide to Complex Numbers

---

(2003-07-30)     B1 = 0.26149721284764278375542683860869585905+
The limit of   [1/2 + 1/3 + 1/5 + 1/7 + 1/11 + 1/13 + ... + 1/p] - ln(ln p)

Mertens constant has been named after the number theorist Franz Mertens (1840-1927).  It is to the sequence of primes what Euler's constant is to the sequence of integers.  It's sometimes also called Kronecker's constant or the Reciprocal Prime Constant.  Proposals have been made to name this constant after Charles de la Vallée-Poussin (1866-1962) and/or Jacques Hadamard (1865-1963), the two mathematicians who first proved (independently) the Prime Number Theorem in 1896.

---

(2003-07-30)     m = 1.451369234883381050283968485892027449493+
Ramanujan-Soldner constant, root of the logarithmic integral:  li(m) = 0

This number is named after Johann von Soldner (1766-1833) and Srinivasa Ramanujan (1887-1920).  It's also called Soldner's constant.

m is the only positive root of the logarithmic integral function "li", which is not to be confused with the so-called offset logarithmic integral:  Li(x) = li(x)-li(2).

li(x)   =	ó	x	dt	=	ó	x	dt
	õ	0	ln t		õ	m	ln t

The above integrals must be understood as Cauchy principal values whenever the singularity at  t = 1  is in the interval of integration...

---

(2004-02-19)     W(1) = 0.567143290409783872999968662210355550-
The Omega constant.

This is the solution of   x = e^-x,  or also   x = ln(1/x).  See Lambert's W function.

The value of the constant could be approximated by iterating the function e^-x, but the convergence is quite slow.  It's much better to iterate the function

f (x)   =  (1+x) / (1+e^x )

which has the same fixed point but features a zero derivative at this fixed point, so that the convergence is quadratic  (the number of correct digits is roughly  doubled  with each iteration).  This is an example of  Newton's method.

---

(2003-07-30)     Feigenbaum Constants
d = 4.66920160910299067185320382046620161725818557747576863+
a = -2.5029078750958928222839028732182157863812713767271500-

What's known as the [first] Feigenbaum constant is the "bifurcation velocity" (d) which governs the geometric onset of chaos via period-doubling in iterative sequences (with respect to some parameter which is used linearly in each iteration, to damp a given function having a quadratic maximum).  This universal constant was unearthed in October 1975 by Mitchell J. Feigenbaum (b.1944).  The related "reduction parameter" (a) is the second Feigenbaum constant...

Feigenbaum Constant :   MathWorld  (Eric W. Weisstein)   |   Mathsoft  (Steve Finch)

---

(2004-05-22)     Brun's Constant:   B = 1.902160582782 (514)
Sum of the reciprocals of  [pairs of]  twin primes:
(1/3+1/5) + (1/5+1/7) + (1/11+1/13) + (1/17+1/19) + (1/29+1/31) + ...

This constant is named after the Norwegian mathematician who proved the sum to be convergent, in 1919:  Viggo Brun  (1885-1978) .

The numerical value and uncertainty quoted above are from the ongoing computation led by Thomas R. Nicely of Lynchburgh, Virginia.

The compact scientific notation used here (and throughout the <Numericana> site) indicates numerical uncertainties by giving an estimate of the standard deviation (s).  This estimate is shown between parentheses to the right of the least significant digit  (expressed in units of that digit).  The magnitude of the error is thus stated to be less than this with a probability of 68.27% or so.

On the other hand, Nicely routinely quotes a so-called  99% confidence level,  which is three times as big.  (More precisely, ±3s is a 99.73% confidence level.)  The following expressions thus denote the same value, with the same uncertainty: 

1.90216 05827 82 ± 0.00000 00015 42 1.90216 05827 82 (514)

Thomas Nicely's computations of Brun's constant began in 1993.  They made headlines shortly thereafter, as Nicely uncovered a flaw in the Pentium microprocessor's arithmetic, which ultimately forced a costly recall of the chip.

Usually, mathematicians have to shoot somebody to get this much publicity.
Thomas R. Nicely   (quoted in  The Cincinnati Enquirer)

---

(2003-08-05)     3.359885666243177553172011302918927179688905+
Prévost's Constant:  Sum of the reciprocals of the Fibonacci numbers.

1/1 + 1/1 + 1/2 + 1/3 + 1/5 + 1/8 + 1/13 + 1/21 + 1/34 + 1/55 + 1/89 + ...

The sum of the reciprocals of the Fibonacci numbers was shown to be irrational by Marc Prévost around 1977, in the wake of Roger Apéry's celebrated proof of the irrationality of z(3), which has been known as Apéry's constant ever since.

The attribution to Prévost was reported by François Apéry (son of Roger Apéry) in 1996:  See The Mathematical Intelligencer, vol. 18 #2, pp. 54-61: Roger Apéry, 1916-1994: A Radical Mathematician available online (look for "Prevost", halfway down the page).

The question of the irrationality of the sum of the reciprocals of the Fibonacci numbers was formally raised by Paul Erdös and may still be erroneously listed as open, despite the proof of Marc Prévost (Université du Littoral Côte d'Opale).

---

(2003-08-05)     0.73733830336929...
Grossman's Constant.   [Not known much beyond the above accuracy.]

A 1986 conjecture of Jerrold W. Grossman (which was proved in 1987 by Janssen & Tjaden) states that the following recurrence defines a convergent sequence for only one value of x, which is now called Grossman's Constant:

a0   =   1    ;     a1   =   x    ;     an+2   =	an
	1 + an+1

Similarly, there's another constant, first investigated by Michael Somos in 2000, above which value of x the following quadratic recurrence diverges (below it, there's convergence to a limit that's less than 1):  0.39952466709679947- (where the terminal "7-" stands for something probably close to "655"). 

a₀ = 0   ;         a₁ = x   ;         a_n+2   =   a_n+1  ( 1 + a_n+1 - a_n )

Footnote: Some early communications by Michael Somos contained a typo in the digits underlined above ("666" instead of "66") which Somos acknowledged nicely when we pointed this out to him (2001-11-24 e-mail).  Unfortunately, the typo remained for several years (until 2004-04-13) in a MathSoft online article, because the original author (Steven Finch) was no longer working at MathSoft and apparently never received our earlier e-mails about this subject...

---

(2003-08-06)     262537412640768743.9999999999992500725971982-
Ramanujan's number:   exp(p Ö163)   is almost an integer.

The attribution of this irrational constant to Ramanujan was made by Simon Plouffe, as a monument to a famous 1975 April fools column by Martin Gardner in Scientific American (where it was claimed that the above had been proven to be exactly an integer, as conjectured by Ramanujan in 1914 [sic!] ).

Actually, this particular property of 163 was first noticed in 1859 by Charles Hermite (1822-1901).  It doesn't appear in Ramanujan's relevant 1914 paper.

There are reasons why the expression   exp (pÖn)   should be close to an integer for specific integral values of n.  In particular, when n is a large Heegner number (43, 67 and 163 are the largest Heegner numbers).  The value n = 58, which Ramanujan did investigate in 1914, is also most interesting.  Below are the first values of n for which   exp (pÖn)   is less than 0.001 away from an integer:

 25:                               6635623.999341134233266+
 37:                             199148647.999978046551857-
 43:                             884736743.999777466034907-
 58:                           24591257751.999999822213241+
 67:                          147197952743.999998662454225-
 74:                          545518122089.999174678853550-
148:                     39660184000219160.000966674358575+
163:                    262537412640768743.999999999999250+
232:                 604729957825300084759.999992171526856+
268:               21667237292024856735768.000292038842413-
522:      14871070263238043663567627879007.999848726482795-
652:   68925893036109279891085639286943768.000000000163739-
719: 3842614373539548891490294277805829192.999987249566012+

Ramanujan’s Constant and its Cousins  by Titus Piezas III  (2005-01-14)

---

(2003-08-09)     1.13198824...
Viswanath's constant was computed to 8 decimals in 1999.

In 1960, Hillel Furstenberg and Harry Kesten showed that, for a certain class of random sequences, geometric growth was almost always obtained, although they did not offer any efficient way to compute the geometric ratio involved in each case.  The work of Furstenberg and Kesten was used in the research that earned the 1977 Nobel Prize in Physics for Philip Anderson, Neville Mott, and John van Vleck.  This had a variety of practical applications in many domains, including lasers, industrial glasses, and even copper spirals for birth control...

At UC Berkeley in 1999, Divakar Viswanath investigated the particular random sequences in which each term is either the sum or the difference of the two previous ones  (a fair coin is flipped to decide whether to add or subtract).  As stated by Furstenberg and Kesten, the absolute values of the numbers in almost all such sequences tend to have a geometric growth whose ratio is a constant.  Viswanath was able to compute this particular constant to 8 decimals.

---

(2003-07-26)     c = 299792458 m/s     Einstein's Constant
The speed of light in a vacuum.  [Exact, by definition of the meter (m)]

In April 2000, Kenneth Brecher (of Boston University) produced experimental evidence, at an unprecedented level of accuracy, which supports the main tenet of Einstein's Special Theory of Relativity, namely that the speed of light (c) does not depend on the speed of the source.

Brecher was able to claim a fabulous accuracy of less than one part in 10²⁰, improving the state-of-the-art by 10 orders of magnitude!  Brecher's conclusions were based on the study of the sharpness of gamma ray bursts (GRB) received from very distant sources:  In such explosive events, gamma rays are emitted from points of very different [vectorial] velocities.  Even minute differences in the speeds of these photons would translate into significantly different times of arrival, after traveling over immense cosmological distances.  As no such spread is observed, a careful analysis of the data translates into the fabulous experimental accuracy quoted above in support of Einstein's theoretical hypothesis.

When he announced his results, Brecher declared that the constant c appeared "even more fundamental than light itself" and he urged his colleagues to give it a proper name and start calling it Einstein's constant.  The proposal was well received and has only been gaining momentum ever since, to the point that the "new" name seems now fairly well accepted.

Since 1983, the constant c has been used to define the meter in term of the second, by enacting as exact the above value of  299792458 m/s.

Where does the symbol "c" come from?

Historically, "c" was used for a constant which later came to be identified as the speed of electromagnetic propagation  multiplied by the square root of 2  (this would be cÖ2, in modern terms).  This constant appeared in  Weber's force law  and was thus known as "Weber's constant".

On at least one occasion, in 1873, James Clerk Maxwell (who normally used "V" to denote the speed of light) adjusted the meaning of "c" to let it denote the speed of electromagnetic waves instead.

In 1894, Paul Drude (1863-1906)  made this explicit and was instrumental in popularizing "c" as the preferred notation for the speed of electromagnetic propagation.  However, Drude still kept using the symbol "V" for the speed of light in an optical context, because the identification of light with electromagnetic waves was not yet common knowledge:  Electromagnetic waves had first been observed in 1888, by Heinrich Hertz (1855-1894).  Einstein himself used "V" for the speed of light and/or electromagnetic waves as late as 1907.

c  may also be called the  celerity  of light:  [Phase] celerity and [group] speed are normally two different things, but the two concepts coincide for light.

For more details, see:  Why is  c  the symbol for the speed of light?   by Philip Gibbs

---

(2003-07-26)     m_o = 4p 10^-7 N/A² = 1.256637061435917295... mH/m
Magnetic permeability of the vacuum.  [Definition of the ampere (A)]

The relation   e_o m_o c ²  =  1   and the exact value of c yield an exact SI value, with a finite decimal expansion, for Coulomb's constant  (see Coulomb's law):

1	=     8.9875517873681764 ´ 10-9   »   9 ´ 10-9   N . m 2 / C 2
4peo

---

(2003-08-10)     Planck's Constant(s):  h  and  h/2p
Quantum of action:    h  = 6.626 068 76(52)   10^-34 J/Hz
Quantum of spin:  h/2p  = 1.054 571 596(82) 10^-34 J.s/rad

A photon of frequency  n  has an energy  hn  where  h  is  Planck's constant.  With the  pulsatance  w = 2pn,  this equals 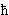 w, where 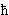   is  Dirac's constant.

The constant 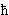  =   h/2p  is actually known under several names: 

• Dirac's constant.
• The  reduced  Planck constant.
• The  rationalized  Planck constant.
• The quantum of angular momentum.
• The quantum of spin.

The constant 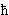(pronounced h-bar) is equal to unity in the natural system of units of theoreticians  (h is 2p).  The spins of all particles are multiples of 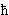  = h/4p  (an  even  multiple for bosons, an  odd  multiple for fermions).

Current technology of the watt balance (which compares an electromagnetic force with a weight) is almost able to measure Planck's constant with the same precision as the best comparisons with the International prototype of the kilogram, the only SI unit still defined in terms of an arbitrary artifact.  It is thus fairly likely that Planck's constant could be given a de jure value in the near future, which would constitute a new definition of the SI unit of mass.

Resolution 7 of the 21^st CGPM (October 1999) recommends "that national laboratories continue their efforts to refine experiments that link the unit of mass to fundamental or atomic constants with a view to a future redefinition of the kilogram".  Although precise determinations of Avogadro's constant were mentioned in the discussion leading up to that resolution, the watt balance approach was considered more promising.  It's also more satisfying to define the kilogram in terms of the fundamental Planck constant, rather than make it equivalent to a certain number of atoms in a silicon crystal.  (Incidentally, the mass of N identical atoms in a crystal is slightly less than N times the mass of an isolated atom, because of the negative energy of interaction involved.)

Peter J. Mohr and Barry N. Taylor have proposed to define the kilogram in terms of an equivalent frequency  n = 1.35639274 10⁵⁰ Hz, which would make the constant h equal to c²/n, or 6.626068927033756019661385... 10^-34 J/Hz.

We tend to think that either h or [rather] h/2p should be given a rounded decimal value instead.  This would make the future definition of the kilogram somewhat less straightforward, but would facilate actual usage when the utmost precision is called for.  To best fit the "kilogram frequency" proposed by Mohr and Taylor, the de jure value of 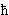could be exactly 1.054571623 10^-34 J.s/rad.

Note: " ħ " is how your browser displays UNICODE's "h-bar" (&#295;)...  OK?

---

(2003-08-10)     Boltzmann's Constant     k = 1.380 6503(24) 10^-23 J/K
Defining entropy and/or relating temperature to energy.

Named after Ludwig Boltzmann (1844-1906)  the constant  k = R/N  is the ratio of the ideal gas constant (R) to Avogadro's number (N).

Boltzmann's constant  is currently a measured quantity.  However, it could possibly be given a de jure value which would define the unit of thermodynamic temperature, the kelvin (K) which is now defined in terms of the temperature of the triple point of water (273.16 .K, exact by definition).

History :

Following Abraham Pais, Eric W. Weisstein reports that Max Planck first used the constant  k  in 1900, in what's now known as  Boltzmann's relation  (giving the entropy S of a system known to be in one of  W  equiprobable  states).

S   =   k  ln{W)

The constant k became known as Boltzmann's constant around 1911.  Before that time, some authors (including Lorentz) had named the constant after Planck.

---

(2003-08-10)     Avogadro Number
Number of things per mole of stuff:  6.022 141 99(47) 10²³/mol

Named after the Italian chemist and physicist Amedeo Avogadro (1776-1856) who formulated what is now known as Avogadro's Law, namely:

At the same temperature and [low] pressure, equal volumes of different gases contain the same number of molecules.

The current definition of the mole states that there are as many countable things in a mole as there are atoms in 12 grams of carbon-12 (the most common isotope of carbon).  Keeping this definition and giving a de jure value to the Avogadro number would effectively constitute a definition of the unit of mass.  Rather, the above definition could be dropped, so that a de jure value given to Avogadro's number would constitute a proper definition of the mole.

---

(2003-07-26)     683 lm/W (lumen per watt) at 540 THz
The "mechanical equivalent of light".  [Definition of the candela (cd)]

The frequency of 540 THz (5.4 10¹⁴ Hz) corresponds to yellowish-green light.  This translate into a wavelength of about 555.1712185 nm in a vacuum, or about 555.013 nm in the air, which is usually quoted as 555 nm.

This frequency was chosen as a basis to define luminous units [matching the eye's photopic response] because it's very special to the human retina in two apparently unrelated respects.  It's very nearly equal to either of the following:

• The frequency at which the retina has the same response under scotopic (low light) or photopic (bright light, standard) conditions. 
• The frequency for which the retina has its maximum photopic response.  (This frequency is thus sometimes called "the most visible light".)

There may be a deep biological reason for which these two frequencies are identical (or nearly identical) but we don't know it.  Please, tell us if you do.

The Power of Light

Primary Conversion Factors

Below are the statutory quantities which allow exact conversions between various physical units in different systems:

• 25.4 mm to the inch :  International inch.  (1959)
  Enacted by an international treaty, effective January 1, 1959.  This gives the following exact metric equivalences for other units of length:  1 ft = 0.3048 m, 1 yd = 0.9144 m, 1 mi = 1609.344 m
   
• 39.37 "US survey" inches to the meter :  "US Survey" inch.  (1866, 1893)
  This equivalence is now obsolete, except in some records of the US Coast and Geodetic Survey.  The International units defined in 1959 are exactly 2 ppm smaller than their "US Survey" counterparts (the ratio is 999998/1000000).
   
• 1 lb   =   0.45359237 kg :  International pound.  (1959)
  Enacted by an international treaty, effective January 1, 1959.  This gives the following exact metric equivalences for other customary units of mass: 1 oz = 28.349523125 g, 1 ozt = 31.1034768 g, 1 gn = 64.79891 mg, since there are 7000 gn to the lb, 16 oz to the lb, and 480 gn to the troy ounce (ozt).
   
• 231 cubic inches to the Winchester gallon :  U.S. Gallon.  (1707, 1836)
  This is now tied to the 1959 International inch, which makes the [Winchester] US gallon equal to exactly 3.785411784 L.
   
• 4.54609 L to the Imperial gallon :  U.K. Gallon.  (1985)
  This is the latest and final metric equivalence for a unit proposed in 1819 (and effectively introduced in 1824) as the volume of 10 lb of water at 62°F.
   
• 9.80665 m/s² :  Standard acceleration of gravity.  (1901)
  Multiplying this by a unit of mass gives a unit of force equal to the weight of that mass under standard conditions approximately equivalent to those that would prevail at 45° of latitude on Earth, at sea-level.  The value was enacted by the third CGPM in 1901.  1 kgf = 9.80665 N  and  1 lbf = 4.4482216152605 N.
   
• 101325 Pa   =   1 atm :  Standard atmospheric pressure.  (1954)
  As enacted by the 10th CGPM in 1954, the atmosphere unit (atm) is exactly 760 Torr.  It's only approximately 760 mmHg, because of the following specification for the mmHg and other units of pressure based on the conventional density of mercury.
   
• 13595.1 g/L (or kg/m³ ) :  Conventional density of mercury.
  This makes 760 mmHg equal a pressure of (0.76)(13595.1)(9.80665) or exactly 101325.0144354 Pa, which was rounded down in 1954 to give the official value of the atm stated above.  The torr (whose symbol is capitalized: Torr) was then defined as 1/760 of the rounded value, which makes the mmHg very slightly larger than the torr, although both are used interchangeably in practice.  The mmHg is based on this conventional density (which is close to the actual density of mercury at 0°C) regardless of whatever the actual density of mercury may be under the prevailing temperature at the time measurements are taken.  Beware of what apparently authoritative sources may say on this subject...
   
• 999.972 g/L (or kg/m³ ) :  Conventional density of "water".
  This is the conventional conversion factor between so-called relative density and absolute density.  This is also the factor to use for units of pressure expressed as heights of a water column (just like the above conventional density of mercury is used for similar purposes).  This density is close to that of natural water at its densest point (SMOW around 3.98°C is about 999.975 g/L) but this is a conventional conversion factor for which the prevailing temperature during measurement is irrelevant (the warning given above for mercury applies here too).
   
• 4.184 J   to the calorie (cal) :  Thermochemical calorie.  (1935)
  This is currently understood as the value of a calorie, unless otherwise specified (the 1956 "IST" calorie described below is slightly different).  Watch out!  The kilocalorie (1 kcal  =  1000 cal) is very often called "Calorie" in dietetics...
   
• 2326 J/kg = 1 Btu/lb :  IST heat capacity of water, per °F. (1956)
  This defines the IT or IST ("International [Steam] Table") flavor of the Btu ("British Thermal Unit") in SI units, once the lb/kg ratio is known.  The value was adopted in July 1956 by the 5th International Conference on the Properties of Steam, which took place in London, England.  The additional relation 1 cal/g = 1.8 Btu/lb defines an IST calorie of exactly 4.1868 J (slightly different from the above thermochemical calorie).  The subsequent definition of the pound as 0.45359237 kg (effective January 1, 1959) makes the IST Btu equal to exactly 1055.05585262 J.