In Fond Memory of
Richard P. Feynman (Nobel 1965)
May 11, 1918 - February 15,1988
The Feynman's Lectures on Physics are based on a famous course of
undergraduate lectures given at Caltech
by Professor Richard Phillips Feynman in the early 1960's.
What Dick Feynman had to say to undergraduates about various physical
units was considered too trivial by the editors and was not included in the published
version of these lectures.
We resurrect it here, from the audio record, as a tribute to Richard P. Feynman.
NOTICE:
The text quoted below was transcribed by Dr. Gerard P. Michon from a copyrighted
6-hour audio record (© 1997 by the California Institute of Technology),
published by Helix Books (Addison-Wesley, Reading, MA) with a printed collection
of edited lectures by Richard P. Feynman, entitled "Six not-so-easy pieces".
Applicable copyright laws allow this short excerpt to appear
here, but a formal permission from the California Institute of Technology and/or other parties
may be required to reproduce any part of this text in a broader context.
For those who want some proof that physicists are human, the proof is in
the idiocy of all the different units which they use for measuring energy.
The Character of Physical Law (1967) R.P. Feynman.
Before I begin the lecture [on spacetime], I wish to apologize for something
that is not my responsibility: Physicists and scientists all over the world have
been measuring things in different units, and causing an enormous amount of
complexity. As a matter of fact, nearly a third of what you have to
learn 1
consists of different ways of measuring the same thing, and I apologize for it.
It's like having money in francs, and pounds, and dollars... with the
advantage over money that the ratios don't change, as time goes on.
For example, in the measurement of energy, the unit we use here
is the joule (J), and a watt (W) is a joule per second.
But there are a lot of other systems to measure energy.
There are at least three different ones for engineers, which I have listed
here.2
The physicists do something else when they want to talk about the energy
of a single atom, instead of the energy of a gross amount of material.
The reason is, of course, that a single atom is such a small thing that to talk
about its energy in joules would be inconvenient.
But instead of taking a definite unit in the same system
(like 10-20 J),
they have unfortunately chosen, arbitrarily, a funny
unit called an electronvolt (eV), which is the energy needed to move an
electron through a potential difference of one volt, and that turns out to be
about 1.6 10-19 J.
I am sorry that we do that, but that's the way it is for the physicists.
 The chemists also talk about the energy per atom.
Since they don't use the atoms individually but large blobs of them,
in cans and barrels, they've chosen a certain number of atoms as a unit.
This number of things is called a mole (mol), and it is
6.023 1023 objects.
The more precise definition, which is now correct
or soon 3 will be,
is that one mole of carbon-12 atoms has a mass of exactly 12 grams.
A mole is just a certain number of things.
So, instead of giving the energy per atom, the chemists give the energy per mole.
It's good, therefore, to know how much energy is a mole of electronvolts.
In other words, if each atom had
one electronvolt of energy, a large number of atoms would have a
reasonable amount of joules, namely 96500 joules per mole.
Incidentally, a mole of electrons has a total charge of 96500 coulombs (C);
these numbers are equal for a reason you have to
figure out.4
The chemists also talk about the energy per atom.
Since they don't use the atoms individually but large blobs of them,
in cans and barrels, they've chosen a certain number of atoms as a unit.
This number of things is called a mole (mol), and it is
6.023 1023 objects.
The more precise definition, which is now correct
or soon 3 will be,
is that one mole of carbon-12 atoms has a mass of exactly 12 grams.
A mole is just a certain number of things.
So, instead of giving the energy per atom, the chemists give the energy per mole.
It's good, therefore, to know how much energy is a mole of electronvolts.
In other words, if each atom had
one electronvolt of energy, a large number of atoms would have a
reasonable amount of joules, namely 96500 joules per mole.
Incidentally, a mole of electrons has a total charge of 96500 coulombs (C);
these numbers are equal for a reason you have to
figure out.4
Now, there is an additional unit that the physical chemists use,
the kilocalorie per mole (kcal/mol), and 23 of those is an electronvolt per atom.
Finally, unfortunately, you have another system for measuring masses.
The mass of an atom, from a chemist's point of view, is given by the mass of a mole
of these atoms.
For example, the mass of carbon-12 is called 12 "atomic mass
units" (u), because a mole of carbon-12 "weighs" 12 grams
(or rather "has 12 grams of mass").
One atomic mass unit represents one gram for every mole of objects,
one gram per mole.
We can measure that in electronvolts also.
"You can't measure mass in electron
volts!" 5
Sure you can,
because of the relation E = mc2 ...
It is useful to know how much energy corresponds to the consumption
of one atomic mass unit of material:
That turns out to be about 931 million electronvolts (MeV).
Incidentally, the rest mass of a proton is 938 MeV,
while the rest mass of an electron corresponds to 0.511 MeV.
The number 938 differs from 931, because a proton has a mass of about 1.008 amu.
I am sorry about the confusion produced by all these systems of units.
I left out, obviously, a large number of different things.
For example, when measuring
luminous 6 energy,
the lumen (lm) is used, which corresponds to about 1.5 mW of
power in the "most visible" light, around 5500 Å (ångströms).
It's all very annoying, but don't worry about it now.
When you need to measure light, just look up in a book what a lumen is.
That's an unfortunate fact that we measure things
in a whole series of different kinds of units.
This causes a lot of confusion.
It's too bad, but I have already apologized, and there is nothing else I can do...
Richard P. Feynman (1961)
Notes :
1 Feynman may well be overstating the case,
but the opposing understatement is so widespread
that we decided to feature this statement as a subtitle for this web page...
2
Consistent "engineering" systems of mechanical units are listed below.
The units of energy and power advocated by Feynman for use at CalTech,
the joule (J) and the watt (W), are metric (SI) units.
The other systems are now obsolete, or are being deprecated:
-
Metric system (SI) for mechanical units (MKS = meter-kilogram-second).
The
unit of force is the newton (N).
-
CGS system (centimeter-gram-second).
The unit of force is the dyne (dyn).
-
British [absolute] system (foot-pound-second).
The
unit of force is the poundal (pdl).
-
Metric-technical system, or "gravitational MKS"
(meter-hyl-second).
The
unit of force is the kilogram-force (kgf).
-
British engineering system, or "English gravitational system"
(foot-slug-second).
The
unit of force is the pound-force (lbf).
3 The CGPM finally adopted this definition of the
mole in 1971.
It is based on the "unified" definition of the "atomic mass unit" (amu)
as 1/12 the mass of a Carbon-12 atom, which was
adopted at the 10th General Assembly of the
International Union of Pure and Applied Physics (Ottawa, 1960)
and subsequently by the
International Union of Pure and Applied Chemistry in 1961.
This replaced two earlier competing definitions of the "amu", both based on oxygen:
The physical amu was defined to be 1/16 of the mass of the Oxygen-16 atom,
while the larger chemical amu was 1/16 of the average mass of an atom of natural
oxygen, with the isotopic composition found on Earth
(99.759% O-16, 0.037% O-17, 0.204% O-18).
The unified amu is only 0.004% more than this chemical amu.
Thus, the chemists got to keep the value of their amu, while the physicists got their
wish in having the atomic mass unit defined in terms of a given nucleus, not a mixture.
The symbol for the unified amu is "u".
A chemical amu was 0.999958 u,
a physical amu was 0.999687 u. [See
sizes.com]
4 Moving a mole of electrons through a potential of
one volt involves an energy equal to a mole of electronvolts. Expressed in joules,
this equals one volt multiplied
by the charge of a mole of electrons, expressed in coulombs.
5 To lift this objection, the "Mev of mass" is
now best abbreviated "Mev/c2", and similar notations could be used for other
mass units obtained from various energy units.
6 In the spoken lecture, Feynman wrongly used the
qualifier "radiant",
instead of the term "luminous" which properly qualifies electromagnetic radiation measured
with the spectral sensitivity of the human eye under normal "photopic" conditions
(when the eye adapts to darkness, it has a different spectral response,
which is called "scotopic").
Luminous power --often called "luminous flux"-- is expressed in lumens,
whereas the corresponding radiant power would simply be measured in watts.
The qualifier "bolometric" may be
used for radiant power, to insist that radiant measurements are meant
to include all energies at all frequencies with the same weight,
which is not the case for luminous measurements.
Current (CODATA-1998) recommended values for the fundamental
constants
and the conversion factors quoted by Feynman:
| Electronvolt (ev) |
1.602 176 462(63) |
10-19 | J |
| - Thermochemical
(1 kcal º 4184 J)a |
23.060 550 07(93) |
| kcal/mol |
| - International Steam Tables (IT, IST)b |
23.045 127 90(93) |
| kcal/mol |
| Avogadro Constant |
6.022 141 99(47) |
1023 | /mol |
| Faraday Constant |
96 485.3415(39) |
| C/mol |
| Atomic Mass Unit (u) |
931.494 013(37) |
| Mev/c2 |
| Mass of the Proton |
938.271 998(38) |
| Mev/c2 |
| 1.007 276 466 88(13) |
| u |
| Mass of the Electron |
0.510 998 902(21) |
| Mev/c2 |
Mechanical Equivalent of Light
(1/683 watt per lumen
at 540 THz)c |
1.464 128 843 338 21... |
| mW/lm |
Wavelength of Light at 540 THz
(c = 299792458 m/s)d |
5551.712 185 185 185... |
| Å |
Precision
is indicated by the estimated standard deviation (between
parentheses),
expressed in units of the least significant digit shown. |
-
In 1935, the thermochemical calorie was defined as exactly equal to 4.184 J.
Historically, the calorie used to be defined as the energy needed to raise a gram of
water by 1°C, just like the Btu (British thermal unit) was the energy to raise a pound
of water by 1°F.
Such definitions depend on the initial temperature and thus gave rise to a multiplicity of
units with the same name.
Also, using a finite increase in temperature (like 1°C or 1°F) in either definition
made the factor of 1.8 reflect only approximately
the effect of switching from the Fahrenheit to the Celsius scale
(the factor is exact for the slopes of the relevant curves, or for equal temperature
increments, not for different finite increments, no matter how small).
This is why the calorie is now defined precisely with the above mechanical
equivalent in joules.
Unfortunately, this definition competes with the 1956 IST definition discussed below.
The trend seems to be that, unless otherwise specified, the calorie is
to be understood as having the above thermochemical definition,
whereas the Btu has the IST definition given in the following note.
-
The 5th International Conference on the Properties of Steam (London, July 1956)
adopted a set of mechanical equivalents to thermal units,
now identified by the abbreviation IT or IST (International [Steam] Tables),
which made 1 Btu/lb exactly equal to 2326 J/kg.
One kilocalorie per kilogram is 1.8 times this ratio, because
there are 1.8°F in 1°C
(this factor applies to ideal units
although the actual energy needed to raise a given mass of water, say,
10°C may be slightly different from 1.8 times what's needed to raise it 10°F).
An IT calorie is thus exactly 4.1868 J.
When the avoirdupois pound was finally defined in metric terms as
exactly 0.45359237 kg (effective January 1, 1959),
the IT Btu became equal to exactly 1055.05585262 J
(namely, 2326 J times the ratio of the pound to the kilogram).
The rarely used "centigrade heat unit" (chu) is 1.8 Btu.
-
The definition of the candela (adopted by
the 16th CGPM in 1979) makes the "Mechanical Equivalent of Light" exactly
one watt per 683 lumens (at 540 THz).
-
The speed of light in a vacuum (c) is Einstein's constant
(the name was advocated by Kenneth Brecher of Boston University, in April 2000).
Because of the (fifth and final) definition of the meter adopted by the 17th CGPM in 1983,
Einstein's constant is now exactly equal to 299792458 m/s.
In 1948, the definition of the ampere by the 9th CGPM gave the
magnetic constant
mo
(the permeability of the vacuum) an exact value of
4p 10-7 H/m.
(One henry per meter is the same as one newton per square ampere.)
The second has been defined in absolute terms since the 13th CGPM,
in 1967.
(The previous astronomical definitions are obsolete.)
The final fundamental step in the construction of the SI system would be to
redefine the kilogram by giving yet another fundamental constant an exact value.
For this transition to happen seamlessly,
current precision
on the known value of such a constant should be about as good as the
precision of comparisons with the international prototype of the kilogram.
We are almost there:
A large device (2 stories high) called a watt-balance
compares a mechanical watt (proportional to a calibrated mass) to an electric watt,
known in
terms of the Planck constant.
The best watt-balances have already determined
Planck's constant
[namely
6.626 068 76(52) 10-34 J/Hz]
to an accuracy (1 s) of about 0.078 ppm,
which is within a factor of 2 or 3 from the best mass comparisons.
The end is in sight.
We are proud to have this page belong to the Feynman Webring, which connects
a number of fine pages which perpetuate the legacy of Richard Feynman in various ways.
Some are more controversial than others:
At this writing, the next site
in this ring happens to feature an essay where
James G. Gilson
presents his own formula (involving two integer parameters)
for the value of the so-called
Fine-Structure Constant
a =
0.007297352533(27)
[whose reciprocal is 1/a =
137.035 999 76(50)].
This dimensionless fundamental constant of Nature
was apparently first introduced in 1915 or 1916, by
Arnold
Sommerfeld (1868-1951).
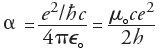
Sommerfeld's Fine-Structure Constant may be viewed as the only
free parameter in QED,
the relativistic quantum theory of the interactions between electrons and photons
(for which Feynman, Schwinger and Tomonaga shared the
1965 Nobel Prize).
In QED, the coupling constant's effective limit is simply the square root of
a, and Feynman was understandably annoyed that QED was
thus based on an unexplained numerical value.
He expressed the wish that a deeper understanding of Nature would
eventually explain that value and/or allow it to be expressed in terms of
known constants, like p or e.
Before and after
Feynman, others have tried to guess such a relation,
possibly hoping that it could be a clue to whatever more general theory may underly
our current understanding of the laws of Nature.
Around 1923,
Sir
Arthur Eddington (1882-1944) "proved" a to be 1/136,
in agreement with early rough estimates.
When subsequently faced with incompatible experimental data,
he amended the "proof" to show that the value had to be 1/137,
so that Punch magazine dubbed him Sir Arthur Adding-One.
See 137 by Charles C. Mann,
or look up the description by
Robert Munafo of the so-called
Eddington
number [the outrageously asserted total number of electrons in the Universe,
as the inverse of the fine structure constant multiplied by a power of two].
The two integers in Dr. Gilson's formula
may be tuned to accurately reflect modern experimental data:
The pair (137,25) was the best match for the midrange of the previous
(1986) CODATA value of a [namely 0.00729735308(33)]
and (137,29) is a good match for the
current one (CODATA 1998, as of 2002).
Interestingly, Gilson quotes Michael Wales,
who had argued that the cube of a
should be the reciprocal of some integer (namely 2573380).
The 1986 CODATA value of a placed Wales' number at
2573379.99(35), which encouraged the conjecture.
However, the more precise 1998 CODATA update gives 2573380.571(29),
which does not stand any reasonable chance of being an integer!
Gilson's formula (and its justifications) may be intriguing at first,
but Gilson is [at best] guilty of wishful thinking when he
presents his formula as a generally accepted fait accompli.
This is simply not so. You've been warned;
you may proceed.
 |
| 2005 |
Photos
from
ESVA (AIP)
|
UMD photos
|
Dissertation
|