(Ashlee of Braithwaite, LA.
2000-05-03
twice)
There is a barber who lives in a small town.
The barber shaves all those men and only those men who do not shave themselves.
Does the barber shave himself?
-
Stay away from the many "cute" answers that do not really address the question:
The barber can't be
a woman (otherwise the term "himself" used in the question would be improper).
It would also be cheating to consider that the barber is a boy (and therefore not a "man")
or any other kind of non-human male creature for that matter...
The dilemma remains (it's not a paradadox, as we shall see):
If the barber doesn't shave himself then he shaves himself.
If he shaves himself, then he doesn't shave himself.
The answer to this classic "problem" is simple:
There cannot possibly be any such barber!
The fact that we are wrongly told at the outset that such a barber exist
just does not make it appear out of thin air in spite of the logical contradictions
his very existence would imply.
This is no more paradoxical than a silly question like:
There's a number whose square is 4 and whose cube is 24. What is it?
Both this and the barber's "problem" are just plain nonsense.
If the existence of something leads to a contradiction,
the thing is thereby shown not to exist and any statements about it are to be considered
either nonsensical or "vacuously true":
Any such barber does shave himself.
Any such barber does not shave himself.
Any such barber has purple hair.
The name of any such barber is Isaac Newton.
All of this is true.
"Vacuously" so.
Russell's Paradox:
More seriously, it is worth pointing out that a fundamental logical
dilemma had to be resolved the same way by the pioneers of set theory:
In what's known as "Russell's paradox", we are asked to consider
the "set" of all sets that are not members of themselves.
Is it a member of itself or not?
Neither answer is acceptable...
Therefore, such a thing can't possibly be called a set!
This paradox was instrumental
in clarifying the (Zermelo-Fraenkel) axioms of modern set theory:
A "set" cannot be just anything we like.
In particular, the axioms imply that no set can be a member of itself.
Therefore, there is no "set of all sets" (it would be a member of itself).
The collection of sets that are not members of themselves thus includes all
sets and it is not a set itself.
That's the way out of Russell's paradox:
"such a set" simply does not exist, exactly like "such a barber"
cannot possibly exist in the barber's dilemma.
Meaningless Statements in Natural Languages:
A related issue about "natural" languages is that there may be
inherently meaningless statements or descriptions in a language
that's allowed to refer to itself.
For example,
"the integers that can be specified in twenty English words or less"
cannot possibly describe any unambiguous set of integers.
Otherwise, there would be such a thing as
"the smallest integer that cannot be specified in less than twenty English words",
which would thus be specified in only 13 English words...
This goes to show that natural or formal languages may include self-contradictory sentences,
not only when they refer to themselves (e.g. "This sentence is false.")
but also when they include other references to the language being used.
Bertrand Russell coined the term Berry paradox
for sentences of this latter type, because of a letter he received from G.G. Berry
introducing the earliest such paradox by discussing, among transfinite ordinals:
The first ordinal that cannot be named in a finite number of words.
You don't have to know what an ordinal is to determine that a sentence like
this one is meaningless.
Its meaning, if it had any, would be an ordinal.
However, by assuming that such a meaning exists, we see that another
ordinal must be described instead.
Thus, the thing can't possibly describe any ordinal.
There's actually no paradox here, just a lack of meaning.
(Melissa of Denver, CO.
2000-11-06)
What is infinity and what does it mean?
(Nagaraj of Anamoose, ND. 2000-11-18)
What is the definition of infinity? Please explain to me in details.
-
Albert Einstein once said that
we can't solve problems by using the same kind of thinking we used
when we created them.
Large
numbers begot the concept,
but they are of no help in the definition of infinity.
Let's try common sense first:
A finite set has n elements, for some nonnegative integer n.
Of course, any set which isn't finite in this sense may be called infinite.
Although this common sense approach is perfectly sound, its seems
the basic distinction between finite and infinite sets ought not
to depend explicitely on the properties of something
as complicated as the integers.
A more fundamental approach was indeed first suggested by
Dedekind,
who turned a well-known paradox (characteristic of infinite sets)
into a natural definition of infinity:
An infinite set is equipollent to one of its proper subsets.
Two sets are said to be equipollent
when there's a one-to-one correspondence between the elements of one and the
elements of the other.
At the most fundamental level (which may not be the most intuitive one)
the existence of infinite sets is built into the
axioms of modern set theory.
Consider the set N of natural integers {0,1,2,3,4,5,6,...}.
The function y = x+1 constitutes a bijection between N and its proper subset
{1,2,3,4,5,6,7,...}.
There's also a one-to-one correspondences between N and the even numbers,
between N and the squares, etc. The set N is thus an example of an infinite one.
The same thing cannot be done with any finite set,
like {1,2,3,4,5,6,7}, which cannot be in a one-to-one
correspondence with any set of fewer than 7 elements.
Tarski's definition of infinity :
The problem with Dedekind's definition of infinity is that
a proof of its equivalence with the common notion
(involving integers) requires the
axiom of choice,
which is normally reserved for advanced nonconstructible proofs.
It's undesirable in a context where even natural integers
are considered too elaborate.
One of the simplest solutions was proposed by
Alfred
Tarski (1902-1983):
Tarski's Definition of Finite Sets (1924)
A set is finite if, and only if, every nonempty
family of its subsets
has a minimal element.
| |
( A minimal element is a set not
containing any member of the family. )
Infinity as a Limit of Large Numbers
If you allow mentally for the existence of such infinite sets (and you should),
you realize that there is no such thing as the "largest" integer.
The process of building larger integers is never ending.
That's what infinity is all about.
This is like the discovery game children play when trying to name the
"largest" number.
Sooner of later, one of them realizes that the game cannot possibly
be won by either player:
Regardless of what number is named, it's always possible to say something
like "twice that" (or "this plus one") and not concede.
Mathematicians routinely study things whose infinite version turns out to be
much simpler than any similar finite version.
One of the simplest examples is the sum (properly called a "series"):
1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + 1/256 + ...
This sum is equal to 1-2-n
when carried out only to its n-th term.
It's simply equal to 1 if all of the infinitely many terms are added up.
When the ancient Greeks were still wrestling with the concept of infinity,
the above sum was underlying something called "Zeno's paradox":
Before an arrow reaches its target it must first travel
half of the distance to it (1/2),
then half of what's left (1/4),
half of what's left after that (1/8), and so forth.
Although there are infinitely many such "steps" the arrow does reach its target...
(Try it!)
ciderspider
(Mark Barnes, UK.
2000-10-11) The Number Line
How do you prove that there are more real numbers than rational ones?
Cantor's so-called diagonal argument is to consider any infinite "list" of real
numbers between 0 and 1 (such a "list" is in one-to-one correspondence with the integers).
A number not in the list may then be constructed whose N-th decimal is
different from the N-th decimal of the N-th number of the list.
Now, make sure that you never choose a 0 or a 9 as decimals for this number
(this is to avoid problems with numbers that have two decimal expansions,
ending with either infinitely many zeroes or infinitely many nines);
you still have 7 digits to choose from at each step.
The number so constructed is definitely not in the list since it has only one
decimal expansion and differs from the Nth number at least in the Nth decimal listed.
This means that any list of reals between 0 and 1, fails to contain all
the reals between 0 and 1.
In other words, there must be more real numbers than there are integers.
(This is one of the simplest and most beautiful proofs of all times.)

Now, to prove that there are more reals than rationals,
you should also prove that rationals may be put in such a list.
There are neater ways to do so, but we'll describe only a
simple-minded scheme here:
At coordinates (p,q) of a whole planar grid, put the value p/q
[use zero as placeholder, if q is zero].
Run through the grid along a square spiral like the one pictured at right.
Put in a growing list each ratio you encounter for the first time as you travel
this way through all possible fractions...
Any given rational will eventually appear in that list,
which is another way to say that all of them belong to the list.

Note: Any set which may be put in such one-to-one correspondence with the integers is
said to be "countable", or to have cardinality
Ào.
(The symbol "Ào" is pronounced
"aleph-null", "aleph-nought" or "aleph-zero" and represents the first
transfinite cardinal,
introduced by Georg Cantor.)
On the probability of rational numbers:
It can be shown that the probability is zero that a randomly chosen real number
will be rational (the statement could be made precise in the proper context
of Lebesgue measure theory).
However, this does not relate at all to the above question,
because it's easy to find a set of numbers which has zero probability but yet contains
just as many elements as the whole set of real numbers.

One such example is the so-called "Cantor set" obtained by removing from a segment
(of numbers from 0 to 1, say) its "middle third" and similarly removing the middle third
of any smaller segment that shows up in this (infinite) process.
Equivalently, you may consider the set of all the numbers
(between zero and one) whose decimal expansions contains
only zeroes and nines.
Its probability is zero, in spite of the fact that this set contains just
as many members as the whole number line
(as a sequence of zeroes and nines is in one-to-one correspondence with a
sequence of zeroes and ones).
(2002-06-04)
What are the fundamental axioms of Set Theory?
-
Well, as Russell's paradox once showed,
we cannot simply call a set anything we like.
The "membership" of a set has to be somewhat restricted;
a set simply cannot be a member of itself (or else we'd run into trouble real fast).
On the other hand, infinite sets must be part of the theory,
if it is to be of any use whatosever... So, it is postulated at the outset that
some sets exists which may be put in one-to-one correspondence with a proper part
of themselves.
Finally, the last axiom listed below (the so-called Axiom of Choice)
postulates that sets need not be explicitely constructible,
but may instead be postulated
to exist as abstract collections of virtual choices.
This is the most controversial axiom of the bunch.
If Set Theory is consistent without the Axiom of Choice,
it is consistent with it as well.
Alternately, weaker versions exists which can replace the axiom of choice.
A proof using the Axiom of Choice
(or, possibly, one of its weaker counterparts) is usually called nonconstructive,
and is rejected by constructivists.
However, such a proof may serve to demonstrate [even to constructivists]
that the negation
of a nonconstructive theorem cannot possibly be shown to be true within the framework
of the rest of Set Theory (since the Axiom of Choice must be consistent with it)...
Axioms of Set Theory
Existence of the Empty Set :
The empty set Æ has no elements.
( $ Æ )
( "x )
( x Ï Æ )
Extensionality :
A set is characterized by its elements.
( "x )
( x Î A
Û
x Î B )
Þ A = B
Separability :
Elements of A with some property
b form a subset of A.
( $ B )
( "x )
( x Î B
Û
( x Î A
& b(x) ) )
Pairing :
Two elements form a set.
( $ A )
( "z )
( z Î A
Û
(z = x) Ú (z = y) )
Union :
The union of a set of sets is the set consisting of all their elements.
( $ C )
( "x )
( x Î C
Û
( $ B Î A )
( x Î B ) )
Power Set :
The power set C = 2 A is the set
of all subsets of A.
( $ C )
( " B )
( B Î C
Û
B Í A )
Regularity :
Set membership is neither reflexive
( A Ï A ) nor circular.
( " A ¹ Æ )
( $ x Î A )
( " y Î x )
y Ï A
[Zermelo, 1930]
Infinity :
An example of an infinite set is
{ Æ, {Æ}, {{Æ}}, {{{Æ}}} ... }
( $ A ¹ Æ )
( " x Î A )
( {x} Î A )
Axiom of Choice :
A set may be formed nonconstructibly, containing
a single element from each nonempty set of a given family of pairwise disjoint sets.
( " A Í
2 E )
( "MÎA "NÎA MÇN=Æ )
Þ
( $ C Í E )
( " B Î
A-{Æ} )
( $ x Î E )
B Ç C = {x}
Further Reading & Online References...
(2005-07-26)
A Set is Strictly Smaller than its Powerset
That's
because no function from A to 2A
can possibly be surjective.
A function f from set A
to set B is said to be surjective
when every element of B is the image of some element
of A.
It is said to be injective when no element of
B is the image of more than one element of A.
Both terms were introduced by the very influential
Nicolas Bourbaki
(the collective pen name of a famous ongoing collaboration of industrious
mathematicians, mostly French, founded on January 14, 1935).
A function that's both surjective and injective is said to be
bijective, or "one-to-one".
(Functions that are surjective, injective, or bijective are respectively called
surjections, injections, or bijections.)
Consider any function
f from set A to its powerset 2A.
Let M be the subset of A consisting of all the
elements x of A such that
x Ï f (x).
Thus defined, M is clearly an element of 2A
which is not the image of any
element x of A.
Our arbitrary function f is thus not surjective.
This shows that there's no surjection from A
to its powerset. 
This much seems obvious for finite set,
but the above proof shows that it holds for all infinite sets as well.
The reader is encouraged to check the above wording for conformity with
the Axioms of Set Theory presented in the
previous article,
assuming only that the concept of a function is familiar enough
(a function from A to B
associates one and only one element of B with each element of A).
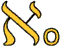
 (2003-11-10)
w and
Ào
(2003-11-10)
w and
Ào
The infinite ordinals and the transfinite cardinals.
Two different approaches make sense of actual
infinite numbers which were both investigated by
Georg
Cantor (1845-1918).
Cardinal Numbers
One may consider natural integers (0,1,2,3,4 ...) to be cardinal numbers.
Each of them describes a property shared by any pair of finite sets that can be put
in one-to-one correspondence with each other.
This is just a fancy way of saying that if you have as many apples as you have oranges,
you may count either the apples or the oranges and you'll come up with the
same number (0 if you have no fruit).
That number is called the cardinality of either set (apples or oranges).
The vocabulary may be intimidating, but the whole thing is really the most basic kind
of numbers, only described in a philosophical way which can be extended.
What about infinite sets?
Can they be "counted" the same way too?
Well, the finite integers are clearly not up to the task.
But can't we just add one more "number"
(using tentatively the "¥" symbol for it)
and say that "¥" is the number of elements
in any infinite set?
Cantor showed that this won't do,
because there are pairs of infinite sets which cannot
be put into one-to-one correspondence with each other.
To be consistent with the very concept of cardinal numbers presented
in the previous paragraph, there has to be more than one
"transfinite" cardinal number.
The symbol Ào (pronounced
"aleph zero", "aleph null", or "aleph nought") was introduced by Cantor to
denote the smallest of these;
it's the number of all the [finite] integers.
An infinite set with this many elements is said to be countable.
An uncountable set is an infinite set which is not countable.
Cantor's diagonal argument
shows that the real numbers (the "points on a line") are uncountable.
His so-called "continuum hypothesis" states that every uncountable set
has at least as many elements as there are points on a line.
Cantor never knew this, but the continuum hypothesis may not
be proved or disproved, it's "undecidable":
We may either assume it's true or assume it's false and no contradiction
will arise, if none was present to begin with.
Cantor's Ordinal Numbers
The second kind of transfinite numbers introduced by Cantor
are called transfinite ordinals.
They may look fancier, but they turn out to be tamer than the transfinite cardinals,
as they do not push against the very boundaries of logic,
the way transfinite cardinals do:
We may start with the following remark:
A natural integer may be represented by
the set of all nonnegative integers before it,
starting with the empty set ({} or Æ)
for 0 (zero) because there are no nonnegative integers before 0.
Then 1 corresponds to {0}, 2 is {0,1}, 3 is {0,1,2}, etc.
For the whole set of nonnegative integers {0,1,2,3...} Cantor introduced the symbol
w.
He did not stop there, since {0,1,2,3...w}
corresponds to another transfinite ordinal, which is best "called"
w+1.
{0,1,2,3...w, w+1} is w+2, etc.
However, you end up doing two different
types of counting if you enumerate a finite set first and an infinite set second or
the other way around...
Addition of Cantor's ordinals is an associative operation
but not a commutative one:
1 + w
= w
¹ w + 1
The maximum number of different results
which can be obtained by changing the order of the terms in a sum of n ordinals
may be tabulated as follows.
The pattern shown in the last pair of lines has exceptions only below n = 15.
Number of different ways to add n ordinals
(A005348)
| 0 | 1 | 2 |
3 | 4 |
| 1 | 1 | 2 | 5 | 13 |
| 5 | 6 | 7 | 8 | 9 |
| 33 | 81 | 193 | 449 | 1089 |
| 10 | 11 | 12 | 13 | 14 |
| 2673 | 6561 | 15633 | 37249 | 88209 |
| 5k + 15 | 5k + 16 | 5k + 17 | 5k + 18 | 5k + 19 |
| 33 ´ 81 k+2 |
81 k+3 |
193 ´ 81 k+2 |
193 2 ´ 81 k+1 |
193 3 ´ 81 k |
The addition of infinite numbers such as w
may also be defined in other ways which retain commutativity.
The most interesting such approach was proposed by John H. Conway,
who defined w essentially as
above, but in the context of so-called surreal numbers,
a very satisfying generalization of the familar concept of "numbers"
(including integers, rationals and real numbers ).
Infinite Numbers among Surreal Numbers
Expressions like
w-1,
2w,
w2,
Öw, or even
ww
have been given a consistent meaning in an extension of the above construction
first described by John H. Conway and presented in the next article...
(2003-11-10)
Surreal Numbers
What's the most general type of ordered numbers?
It turns out that a more general type of number line
(as opposed to unordered things like complex numbers) is conceptually
easier to define than the familiar real numbers.
With the right approach,
it's actually easier to include infinitesimals and transfinite ordinals
than to rule them out...
The term surreal numbers was coined by Donald E. Knuth in 1973 to describe
the beautiful construct of
John
H. Conway, who gave simultaneously a recursive definition of the numbers
and of the order between them...
Conway introduces the compact notation
x = { L | R } =
{ x R | x L }
for what is called a
game;
an ordered pair of two sets L and R, given either by name or by listing their
elements, all of which are [simpler] games themselves...
An element of L or R may be called a left or right option of x.
Numbers are then defined as special games whose options are other numbers,
and which lay "between" their own left and right options, in the following
sense, recursively defined:

Part of Conway's notation is standard: If L or x L
is a set, then L+y is universally understood as the set of all elements obtained
by adding y to an element of L, just like E+F is the set whose elements
are sums of an element of E and an element of F.
If desired, the rest of Conway's notation could easily be translated into
the standard notation of set theory,
by stating that a number may stand for a single-element set within
the "first level" of a "{...|...}" notation and that a comma ( , )
is synonymous with the "union" operator
( È ) in that same context.
Here are single-line definitions of some basic arithmetic operations:
- Sum: x + y =
{ x L + y , x + y L |
x R + y , x + y R }
- Opposite of a number: -x =
{ -x R | -x L }
- Product: xy =
{
xL y + xyL -
xL yL ,
xR y + xyR -
xR yR |
xL y + xyR -
xL yR ,
xR y + xyL -
xR yL }
Well, nobody said this was easy to work with, but it sure is beautiful...
As part of a Grothendieck
universe, surreal numbers
form a set.
This set is certainly larger than most, but it's not an unwieldy
proper class.
Surreal Numbers
(2005-07-09)
Numbers
From integers to real, surreal, and
hypercomplex numbers.
The most rudimentary numbers are the counting numbers
(1, 2, 3, 4 ...) but it's probably best to let
the story begin with the natural numbers (0, 1, 2, 3 ...)
in spite of the fact that zero
is a sophisticated concept of relatively recent origin.
Negative integers originated after the fractions and
constructible numbers which result from the application
of classical rules (compass and straightedge)
to Euclidean geometry.
Algebraic numbers were also considered before negative numbers were accepted
(along with complex numbers, during the Renaissance).
Real numbers were invented in the 19th century to close all "gaps" in the
number line.
(If the real numbers are divided into two sets L and R such that no element of L exceeds
an element of R, then L and R have one element in common.)
Archimedes
attributes to
Eudoxus
what's now called the Archimedean
property of ordinary numbers: Some integral multiple of any given positive quantity
always exceeds another such quantity.
The surreal numbers, mentioned above,
are not Archimedean, as they include infinitesimal positive
quantities whose product by any integer can't exceed a
number like 1
(likewise, no integer exceeds an infinite surreal quantity).
Totally-Ordered Number Classes
(each one contains those below it)
| Number Class | Structure | Countable | Complete | Archimedean |
| Surreal Numbers | Field | No | Yes | No |
| Real Numbers | No | Yes |
| Algebraic Numbers | Yes | No |
| Constructible Numbers |
| Rational Numbers |
| Integers | Ring |
| Natural Integers | Monoid |
| Counting Numbers | Semigroup |
The so-called Cayley-Dickson construct doubles
the dimension of a previously established set of numbers,
by considering ordered pairs of such numbers
and defining their sums, products and conjugates
(the "conjugate" of z is denoted z*) in the following way.
This ensures that the product of a number and its conjugate is a nonnegative
real number, defined to be the square of its norm...
|
( a , b ) + ( c , d )
| = |
( a + c , b + d )
|
|
( a , b ) ( c , d )
| = |
( a c - d b* ,
a*d + c b )
|
|
( a , b )*
| = |
( a* , -b )
|
Hypercomplex Numbers: Normed Division Algebras
(multidimensional
numbers with real coordinates)
| Set | Dimension | Commutativity | Associativity |
| Cayley's Octonions | 8 | No | Alternative |
| Quaternions | 4 | Yes |
| Complex Plane | 2 | Yes |
| Straight Line | 1 |
Arguably, the above process should stop with the octonions, as the
next step up yields a construct (the sedenions) where two
nonzero elements may have a zero product.
It would seem abusive to call such things numbers...
The qualifier may even be dubious for octonions
whose multiplication is only alternative :
"x
"y
(xx)y = x(xy) and y(xx) = (yx)x
By contrast, the noncommutativity of quaternions is acceptable
and interesting; the resulting algebraic structure
is called a skew field, and it repays study.
- Sir William Rowan
Hamilton
(1805-1865) invented the quaternions on October 16, 1843.
The
next day, he told John T. Graves about it...
- John T. Graves (1806-1870)
came up with octonions on December 26, 1843.
They were rediscovered by Arthur Cayley in March 1845.
Interestingly, the term associativity was coined by Hamilton
in 1843, shortly before he found out that octonions failed
to have this basic property:
"x
"y
"z
( x y ) z = x ( y z )
(2005-07-19)
Von Neumann - Bernays - Gödel set theory
(NBG)
A set is a member of a class.
A proper class isn't a member of anything.
The theory originated with John von Neumann (1925).
It was then modified by Paul Bernays (1937) and simplified
by Kurt Gödel (1940).



