Algebra
(R. P. of San Luis Obispo, CA.
2001-01-23)
(M. M. of Gresham, OR.
2001-02-11)
Why is zero factorial equal to one?
The quantity n! (pronounced "n factorial" or "factorial n") is
defined as the product of the n integers from 1 to n.
The basic reason why 0! equals 1 is that it's merely a product of 0 factors;
Such an empty product must be equal to 1,
just like a sum of zero terms (an empty sum) must be equal to 0. Let me explain:
The product of (n+1) factors is clearly equal to the product of the first n factors
multiplied by the last one. This is "clear" to everybody when n is 2 or more.
To make this work for n=1 we have to state that a "product" consisting of a single factor
is equal to that factor.
It follows (for n=0) that a product of zero factors multiplied by any number x must
be equal to x. Therefore, the product of zero factors must be equal to 1.
(The same reasoning for sums leads to the conclusion that a sum of zero terms is equal to 0,
which is less shocking to most people than the corresponding result for empty products.)
Defining n! as a product of n factors (1,2, ... n) when n is nonzero thus implies that the
only consistent definition of 0! is 0!=1.
Another "advanced" argument is to define factorials in term of the analytic
Gamma function ( G ),
whose properties also imply a value 0!=1.
massxv2
(2002-05-13)
and Diane302
(Fort Worth, TX.
2002-05-14):
Why is any number [including 0] raised to the power of 0 equal to one?
If you multiply xn by x, you obtain xn+1.
So, the product of x0 and x is x [= x1].
If x is nonzero, x0 must therefore be equal to 1.
Furthermore, we also have:
00 = 1
This seems to bother some people offhand (including a few
textbook authors,
who should know better),
but x = 0 is not an exception to the above rule:
It's indeed true that 00 = 1 .
The most fundamental explanation is that an empty product
[the product of no factor(s), which is what a zeroth power is]
cannot possibly depend on the value of any factor since
you are not using any such factor to form the "product".
Thus, the value obtained for the zeroth power of any nonzero x
must also be the correct value when x is zero.
In spite of a superficial similarity, this is not a "continuity argument"
(such analytical arguments will not work past the elementary level
where exponents are only integers, because it so happens that
the two-variable function x y
cannot be made continuous at the point x = y = 0, as discussed below).
Instead, the above argument rests purely on basic logic [set theory and algebra].
I could leave it at that and rest my case, but I know that the above
logical argument
is often unable to overcome the psychological reluctance to accept
the fundamental fact we're discussing here...
Although the mathematical case is closed,
some people may find it helpful to take a lexicographer's approach and discover that
unity is the value of zero to the power of zero which is implied in a number of
familiar mathematical contexts.
View the following examples only as a supplement to the above fundamental logic,
which illustrates
that the relevant mathematical discourse is always consistent with it
(because it's based on it)...
- According to the binomial theorem,
(1-1)n
is the alternating sum of the coefficients
in a line of Pascal's triangle.
The result is zero, except for the top line where it's equal to unity
(namely, the only nonzero coefficient in that top line).
- An expression like
å anxn
is understood to have value ao when x = 0.
- etc.
Let's grok
(in fullness):
grok 
tr.v. grok·ked, grok·king, groks. Slang.
To understand profoundly through intuition or empathy.
To assimilate everything about something to the deepest possible extent,
becoming as one with the subject of focus.
[ Stranger
in a Strange Land (1961) by Robert Anson
Heinlein ]
The
American Heritage Dictionary (online)
Do you grok that?
The modern expression xy is defined only under one [or both]
of the following conditions.
(In particular, 0y is not defined unless y is a
nonnegative integer.)
- x is positive (in which case y could be any real or
complex number).
- y is an integer (if y is a negative integer, x must be nonzero).
Lest the reader object that 0y should be defined as
the limit of xy as x®0+,
we'll point out that, when
y is the imaginary number i, we obtain exp(i Log(x)),
which keeps going around the unit circle,
without approaching any limit...
When the exponent (y) in the expression
xy happens to be an integer, the base
(x) can be any number whatsoever
(positive, negative or even complex}
except that it can't be zero when y<0.
In that elementary context, it's clear that algebraic consistency imposes
the zeroth power of any number (positive, negative or complex) to be unity.
There's no reason to make an exception for zero that would introduce an arbitrary
and needless discontinuity at the origin for the function
f(x) = x0, which is everywhere else equal to 1.
As we generalize the notion of exponentiation, this elementary perspective must be
retained, unless it is found to be incompatible with the more general framework.
If such a contradiction occurred,
we would have either to renounce the generalization or
introduce an unwelcome exception to the elementary concept.
Fortunately, were are not faced with this difficult choice in the case
of exponentiation. Read on.
Historically, fractional values of the exponent
were first introduced, in the late Middle Ages, by the Frenchman
Nicole
Oresme (1323-1382).
However, the base x must be positive when fractional exponents are used,
or in any context where they are not ruled out.
The reason why this has to be so is clear only in the context of complex analysis.
The nature of the essential
discontinuity of the two-variable function
f (x,y) = xy
about the origin (x = y =0)
is probably best grasped by considering the curves where this
quantity is constant, for positive values of x and y near the origin [more precisely,
when x is positive and less than 1].
The cartesian equation of such a curve is y = a / ln(1/x) for some
nonnegative value of the parameter a;
all these curves include the origin in their closure!
Along any of them, the value of the function is constant: It's equal
to exp(-a), which can be essentially anything you want between
0 (excluded) and 1 (included).
This does imply that the two-variable function f does not have
a limit at the point (0,0), since you have points in any neighborhood of the
origin for which the value of f is close as you wish from any
choice of a number in the interval [0,1].
The designers of some pocket calculators have decided to make it illegal to raise
zero to the power of zero on their machines.
This is either a misconception on their part, or an overly cautious [misguided]
approach to "fix" the fact that the function "x to the y" is not continuous
about x = y = 0,
which makes it behave erratically when previous rounding errors
have been made.
(Consider that the function equals 0 when x is 0 and y is 0.0000000001,
but it's 1 when x is 0.0000000001 and y is 0).
This is a misguided concern because the problem is with whatever prior rounding errors
occurred, not with the discontinuous function itself.
The fundamental flaw is with the so-called "floating-point" approach of such calculators
(and/or computer languages) which involves a drastic loss of accuracy when nearly
equal quantities are subtracted; It's up to the user to avoid such cases
(numerical analysis is not always easy, even with the help of a computer).
We've also been told about electronic devices which wrongly return an
"infinite" value for the zeroth power of zero
probably because of some careless internal error
propagation when attempting to take the "logarithm of zero",
as a misguided intermediate step...
chormpy (N. N. of New Zealand.
2000-10-21)
Explain what complex numbers are, in terms an idiot could understand.
Picture this. We are both facing each other in an open field and you are challenging
even the existence of negative numbers, let alone complex numbers:
- I ask: "Can you take two steps towards me?"
- You say "Yes" and you do. So nice of you. I thank you.
- Then, I ask you to move "minus two" (-2) steps towards me.
- You smile (having understood what negative numbers are).
You say "Yes", and you take two steps back to your original spot.
- It's my turn to smile: "Can you take an imaginary step towards me?"
- You don't smile. You say "Huh?"...
However, after a lot of thinking you take a step sideways Nice job!
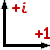
It's ultimately a matter of convention to choose whether
a "forward" imaginary step is to the left or to the right.
However, the universal convention is that a positive imaginary step is a
step sideways to your left (a negative imaginary step is to your right).
In other words, complex numbers are to the plane what real numbers are to the line.
They just describe position and motion in the plane the same
way real numbers do on a line.
In that context, imaginary simply means sideways...
Adding two complex numbers is easy: The total number of steps taken in the "real" direction
is obviously the sum of all steps taken in the real direction. The same applies to the
imaginary direction. In other words, each component (real or imaginary) of the sum is
the sum of the corresponding components of the complex numbers you're adding.
Things become only slightly more delicate if you worry about "multiplying" such "numbers"
together. Just think about it this way: What's the product z of two numbers x and y?
Well it's the number z which is to y what x is to 1! (Isn't it?)
Picture what this means in the complex plane and say x=2+i
(I move two steps forward and one step to the left).
Multiplying any number y by x is like using x as your new "unit" step.
In other words, you are using a new "grid" where each step is of length
Ö5
(that's the length of x, because of the Pythagorean Theorem),
while the whole grid has been rotated about 26.565°,
to align x with the "forward" direction. If you go 3 steps forward and one step right
(corresponding to the complex number y=3-i) in that new grid where do you end up?
Well, you end up on the point of the plane which, by definition, is the product of x and y.
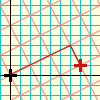
In the "old" grid the rules of complex arithmetic tell you that
z = xy = (2+i)(3-i) = (6+1)+i(3-2) = 7+i
You could have taken 7 "original" steps forward and one step to the left and would have
ended up at the same location.
Draw this on paper --once in your life-- and admire the "coincidence" of the two
results, obtained with or without an intermediate grid.
On 2000-10-22, Chormpy wrote:
Thank you for your answer, Gerard.
Although I'm still far from actually understanding,
your answer did clear things up a little.
It helped me to understand some of the other examples
and explanations of complex numbers I've found.
|
The terms real number and imaginary number
(nombres réels et nombres imaginaires)
were coined by René Descartes in
"La Géometrie" (1637).
Jon
Ball (2002-10-22)
Using the
Golden Ratio (f)
to solve z5 = 1.
How do you express the 5 fifth roots of unity in terms of
f = ½(1+Ö5) ?
Using the fact that cos(2p/5) =
½(f-1) and the relation
f2 = f + 1,
it's not difficult to show that the 5 fifth roots of unity are:
1,
½ [ f-1 ± i
Ö(2+f) ],
and
½ [ -f ± i
Ö(3-f) ].
The 10 tenth roots of unity include the above and their 5 opposites...
ciderspider (Mark Barnes, UK.
2000-11-04)
Does the equation x=2p
have an infinite number of complex solutions?
No, it does not.
The function 2z
can only be defined as exp(ln(2) z).
Just like the exp function itself, it's
single-valued over the entire complex plane.
There's nothing to "solve", the value of x is simply
some real number: 8.824977827...
The only possible source of confusion is the use of the numerical
constant ln(2) in the above definition...
Since the extension of the ln function to complex arguments
is indeed multivalued, why not take any of the "other" values of ln(2)
and go on from there?
I won't skirt the issue, but I must first stress that,
when z is not an integer,
the expression az is never ever used by professionals
(except for fun) unless a is a positive real number.
It is then defined to be exp(ln(a) z),
where ln(a) is the (real) natural logarithm of a.
If you take "another" value of ln(2)
(say: ln(2) + 2pi )
to define your own base-2 exponential,
you simply get another single-valued function which is different from everybody else's.
You could define infinitely many such functions, but so what?
The values of two such functions at the same point
(p or any other point)
have no more reason to be declared "equal" than
Ö4 and -Ö4 do.
In fact, the square root function
is an introductory example of a function which, like the logarithm function, does not
present a problem for (positive) real numbers, but which cannot be generalized
to a continuous function over the whole complex plane.
As explained in the next article,
a continuous generalization of the square root function involves an
entirely new domain of definition (called a Riemann surface).
For the square root function, the Riemann surface consists of the origin and
nonzero points identified as (r,q)
where r is the [positive] distance to the origin and the "angle"
q is understood "modulo 4p",
so that (r,q) and (r,q+2p)
identify two distinct points with different square roots
(which are opposite of each other).
Loosely speaking this surface is composed of two sheets and you end up
back to the same point if you go around the origin an even number of times.
In the case of the logarithm function,
the Riemann surface has infinitely many sheets;
you may visualize it as a flattened helicoid whose nonzero points are
identified as above by a couple (r,q)
except that different values of the real number q
will always identify different points of the surface.
What this means, in concrete terms, is that whenever you use a logarithm
you must absolutely refrain from adding an arbitrary multiple of
2p to the "angle" of the argument.
This is allowed in the complex plane, but prohibited on the relevant Riemann surface
over which the continuous logarithm function is defined.
Do think about Riemann surfaces and you are safe under the umbrella of mathematical rigor.
Forget about this fundamental point and you are bound to produce a number
of false proofs, not always for a recreational purpose...
silenteuphony (2003-07-20)
Generalizing the Square Root Function...
May the square root function ( Ö )
be generalized to negative numbers?
The short answer is no.
Such misguided generalizations would invalidate familiar properties established in the realm
of nonnegative real numbers, where the square root of a number x is unambiguously
defined as the positive number whose square is equal to x.
Among the casualties would be one of the most trusted relations:
Öu Öv =
Ö(uv):
Indeed, if a definition of Ö(-1) could be given which was
consistent with this relation, we would have:
Ö(-1) Ö(-1) =
Ö1,
so that the square of Ö(-1) would be 1
instead of (-1)...
There is a number whose square is -1,
namely the imaginary number i [note that its opposite
-i would do just as well].
However, it is abusive to denote it Ö(-1) for a
number of reasons, including the one given above.
Unfortunately, this has not stopped a number of
otherwise distinguished authors from doing so,
in order to bypass a more proper introduction to what imaginary
and complex numbers really are.
(See above for our own attempt at such an introduction.)
What about the "square root" of a complex number?
If we insist on defining a square root
(sqrt or Ö )
as a single-valued function over the complex plane,
the best we can do is accept discontinuity
(jumping from y to -y) on some kind of curve going from the origin to infinity
(e.g., one half of a straight line).
This annoying issue was cleverly resolved by Bernhard Riemann (1826-1866)
who stated essentially that the "correct" domain of sqrt was not
the complex plane itself, but (roughly) two copies of it,
properly interconnected topologically.
Each such "copy" (loosely speaking) is called a Riemann sheet and the whole thing
is the Riemann surface for the sqrt function.
This surface may be rigorously described as consisting of the origin, together with
the set of ordered pairs (r,q)
where r [the distance to the origin] is positive
and q is a real "angle"
modulo 4p
(whereas a similar definition of the ordinary single sheet complex plane
would specify that q
is "modulo 2p").
The beauty of this approach
is that sqrt is defined and continous everywhere on its two-sheet domain
(its range is the ordinary single sheet complex plane).
The "two-sheet" Riemann surface for the square root function is totally different from
the set of complex numbers.
Loosely speaking, you end up on the same point only if you travel an even
number of times around the origin.
If you wish, you may identify a point on the surface using a notation like
(r,q) where q
is between 0 and 4p,
although it's probably better to make no such restriction and state that the second number
is understood "modulo 4p" (as stated above)
so that the point (r,q)
is identical to (r,q+4kp)
for any integer k...
Points on the two-sheet Riemann surface have square roots that are ordinary complex numbers;
the square root of the point (r,q)
is defined as the complex number
(Ör) exp(iq/2).
Therefore, (r,q) and (r,q+2p)
have two different square roots that are opposite of each other.
Notice that arithmetic on the Riemann surface has its own rules;
in particular, the product of u = (a,a)
and v = (b,b) is
uv = (ab,a+b),
where a+b is understood modulo 4p.
This is how we maintain the validity of properties like
ÖuÖv =
Ö(uv).
A nonzero complex number is associated with
two distinct points of the Riemann surface, which have different square roots
(opposite of each other), so
the "nice" definition of square roots over the Riemann surface does not resolve the
sign ambiguity for ordinary complex numbers.
One "deep" explanation for the impossibilty of defining a continuous generalization of
the square root function over complex numbers is that the relevant
Riemann surface and the complex plane are not
topologically equivalent
(there's no bicontinuous one-to-one correspondence between the two things).
If you choose to define Ö
on the domain of complex numbers rather than on the proper Riemann surface,
your "square root" function cannot be continuous and the "square root" of a product
is not necessarily equal to the product of the "square roots" of its factors.
There's no way around this...
A cardboard model of the Riemann surface for the sqrt function is easy to make
(but not easy to describe; the surface "goes through" itself along one line).
It's pretty too; I am keeping the one I made years ago on a shelf next to my desk,
as a constant reminder of the above fact in the realm of "complex variables"...
(M. M. of Salem, MA.
2000-10-11)
Two numbers have a product of 19551 and a sum of 280.
Without determining the numbers, find their difference.
-
If P, S and D are the product, sum and difference of the two numbers, then:
S2 - D2 = 4P
Therefore, in this case, D2 is
2802-4´19551 or 196.
The difference D between the two numbers is thus 14.
(Don't be silly and object that it could also be -14)
You may want to prove the relation S2 - D2 = 4P
by noticing that:
(x+y)2 - (x-y)2 =
(x2+2xy+y2) - (x2-2xy+y2) = 4 xy
ì
í
î | |
A = x + y +z
B = x 2 + y 2 + z 2
C = x 3 + y 3 + z 3 |
FlyingHellfish (Atlanta, GA. 2002-10-08)
Find the value of D = x4+y4+z4,
given the relations at right, in particular when A=1, B=2, and C=3.
Introducing the elementary symmetric functions,
U = x+y+z, V = xy+yz+zx, and W = xyz. , we have:
A = U,
B = U2-2V,
and C = U3-3UV+3W.
Conversely,
U = A,
V = (A2-B) / 2,
and W = (A3-3AB+2C) / 6.
Since
D = U4-4U2V+4UW+2V2,
we have
D = (A4-6A2B+8AC+3B2) / 6.
For the particular case A=1, B=2, C=3, this means D = 25/6.
The quantities x, y and z are the 3 zeroes of
X3-UX2+VX-W
(in the numerical case above, two of these are complex numbers).
Any symmetrical polynomial of such roots is also a polynomial in U,V,W,
and its value may thus be obtained without solving the cubic equation.
This remark may be generalized to any number of variables...
The Elementary Symmetric Functions:
For m variables, the nth
elementary symmetric function (sn )
is defined via:
| s0 = 1
s1 = |
| Xi
s2 = |
| XiXj
s3 = |
| XiXjXk etc. |
If n>m, sn = 0
(since there are no products of n distinct variables to sum up).
The m variables X1, X2, ... Xm
are clearly the roots of the polynomial [in x]:
| m |
|
m |
|
| Õ |
(Xi - x)
= |
å |
sm-n (-x)n |
| i = 1 |
|
n = 0 |
|
A polynomial in m variables which remains unchanged under any permutation of the variables
is called symmetrical.
Any such polynomial can be expressed as a polynomial of
the above elementary symmetric functions.
Such is the case, in particular,
for the sum of the p-th powers of all the variables (Sp ):
S1 = s1
S2 = s12 -
2s2
S3 = s13 -
3s1s2 + 3s3
S4 = s14 -
4s12s2 + 4s1s3
+ 2s22 - 4s4
This last relation gave us D = S4 in the above case of 3 variables
(s4 = 0).
To extend the list in a systematic way, we may observe that the following
results (known as Newton Identities or Newton-Girard Formulas)
hold for any m:
| |
m |
|
| 0 = m sm +
|
å |
sm-n (-1)n Sn |
| |
n = 1 |
|
This is true for m variables,
because each is a root of the above polynomial
(the right-hand side is thus obtained by summing m zero values of that polynomial).
This holds for less than m variables
(the result for m variables holds if some of them are set to zero)
and also for more than m variables,
because of symmetry and degree considerations which we won't go into...
For example:
S5 =
s1S4 -
s2S3 +
s3S2 -
s4S1 +
5s5
which yields the expression:
S5 =
s15 -
5s13s2 + 5s12s3
- 5s1s4
+ 5s1s22
- 5s2s3 + 5s5 [7 terms]
Such expressions of power-sums in terms of the elementary symmetric polynomials
are known as Girard-Waring expansions
(published in 1629 by
Albert
Girard and between 1762 and 1782 by
Edward
Waring).
If p is the partition function,
Sk expands into p(k) terms: 1,2,3,5,7,11,15,22,30,42,56...
S6 =
s16
- 6s14s2
+ 6s13s3
+ 9s12s22
- 6s12s4
- 12s1s2s3
+ 6s1s5
- 2s23
+ 6s2s4
+ 3s32
- 6s6 [11 terms]
S7 =
s17
- 7s15s2
+ 7s14s3
+ 14s13s22
- 7s13s4
- 21s12s2s3
+ 7s12s5
- 7s1s23
+ 14s1s2s4
+ 7s1s32
- 7s1s6
+ 7s22s3
- 7s2s5
- 7s3s4
+ 7s7
Apparently, no coefficient coprime with k exists in the expansion of
(Sk-s1k ).
The expansion may be given
in the form of a determinant: |
Sk
= |
 |
s1
2s2
3s3
4s4
...
...
ksk |
1
s1
s2
s3
...
...
sk-1 |
0
1
s1
s2
...
...
sk-2 |
0
0
1
s1
...
...
sk-3 |
|
0
0
0
0
...
1
s1 |
|
(S. M. of Bagdad, KY.
2000-10-18)
Find 6 numbers in continued proportion.
Their sum is 14 and the sum of their squares is 133.
Three or more numbers are said to be in "continued proportion"
when the ratio of one term to the previous one is a constant R.
This is now more commonly called a "geometric progression" of ratio R.
If A is the first of 6 such terms, their sum is A(R6-1)/(R-1)
and the sum of their squares
is A2´(R12-1)/(R2-1).
(That's assuming that R differs from 1, but it's easy to check that R=1 does not yield any
solution to the problem at hand.)
If we are told that the former is 14 and the latter is 133, we may solve this using a pair
of relations giving (1) the first quantity and (2) the ratio of these two. Namely:
(1) 14(R-1) = A(R6-1) and
(2) 133(R+1) = 14A(R6+1)
Substituting in (2) the value of AR6 obtained from (1)
(namely 14(R-1)+A) --or the other way
around-- we obtain the relation 9R+4A=47.
(Incidentally, this same relation would hold regardless of the length of the continued
proportion.) Either of the above equations then becomes:
9R7-47R6+47R-9=0.
The obvious root R=1 is to be ruled out, as remarked at the outset
(so we could freely divide by R-1). Dividing by (R-1), there remains to solve a polynomial
equation of degree 6, namely:
9R6-38R5-38R4-38R3-38R2-38R+9=0
Clearly, if R=K is a solution, R=1/K is another one.
Both roots correspond to the same solution
of the original problem but with the 6 numbers listed "forwards" or "backwards".
This calls for changing the unknown variable to X=R+1/R
(which gives X2=R2+1/R2+2 and
X3=R3+1/R3+3X);
if we have a solution for X, it's only a matter of solving a second degree equation to
recover a pair of solutions for R. Dividing the above equation by R3 thus gives
9(X3-3X)-38(X2-2)-38X-38=0, or
9X3-38X2-65X+38=0.
That's still a mouthful but it's only of the third degree so we could solve it with
algebraic methods! I hate doing this, so I'll just give the three roots approximately
(they happen to be all real):
5.41246229893, 0.469896647164, and -1.66013672387.
Now, a solution in X corresponds to a pair of real solutions in R when the equation
R2-XR+1=0 has real solutions. This happens only when X2-4 is positive.
Therefore only the solution X=5.412... is to be retained if we are only interested in real
solutions. This corresponds to the solution R=5.2209925253737229 (or the inverse of this to
list the numbers backwards) and A=(47-9R)/4.
The unique pair of solutions is thus composed of the following 6 numbers listed either
as below or in reverse order (last digits not guaranteed):
11.319041915071,
2.1680145008661,
0.41525483439613,
0.079536634750585,
0.015234202575022,
0.002917912349556.
Now, you may check (I did!) that the sum of the above is indeed 14 and the sum of their
squares is indeed 133...
tenorboy
(Todd A. Moore.
2002-05-19)
In an alley way, a 12 ft ladder leans against a building on one side;
its bottom is on the ground against another vertical building across the alley.
Similarly, a 10 ft ladder leans in the other direction across the alley...
The ladders intersect 4 ft off the ground. What's the width of the alley?
-
Let x be the width of the alley and ux the horizontal distance from the bottom of
the 12-ft ladder to the plumb line at the intersection;
(1-u)x is the corresponding quantity for the second ladder.
Remark that the 4-foot plumb line is equal to u times the top height of the first ladder
and (1-u) times the top height of the second one
(because of the two pairs of similar triangles involved).
In other words: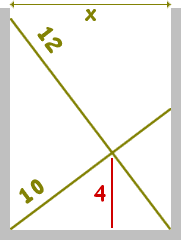
4 = u Ö(122-x2)
and
4 = (1-u) Ö(102-x2)
Eliminating u, we obtain:
1 / Ö(122-x2)
+
1 / Ö(102-x2)
= 1/4
We may use this equation directly to find the solution numerically,
with ludicrous precision:
x = 7.2575891083169677047316337322... ft.
Alternately, we may obtain a polynomial equation,
by eliminating the above two radicals:
First put one radical by itself on one side of the equation;
squaring both sides will then eliminate that first radical.
Isolating the remaining radical on one side and squaring again gives
a rational expression without radicals.
This double squaring gives a quartic [= degree 4] equation
in the variable y = x2.
Because the equation is only a quartic,
it can be solved algebraically, although everybody (including myself) hates to do so.
For the record, here's the quartic:
y4 - 424 y3 + 64912 y2 - 4200448 y + 95420416
= 0
Note that this quartic equation may include roots which do not correspond to solutions of
the original problem...
Indeed the double squaring does introduce just such a spurious solution here
(corresponding to x around 9.6668,
which is clearly not a solution of our original equation).
All told, in this age of computers and nifty scientific calculators,
it's probably best to stick with a simple equation (like the one we first gave)
rather than insist on some not-so-simple polynomial relation with a few irrelevant roots...
|
