Nomenclature & Etymology
(Jon of Visalia, CA.
2000-10-18)
What is the origin of the word "algebra"?
"Algebra" comes from the arabic title of a book by the Persian mathematician
Abu Abd Allah Muhammed ben Musa al-Khwarizmi (c.783-fl.847)
which is transliterated as: Kitab al-mukhasar fi hisab al-jabr wa'l muqabala
(Overview of Calculation by Transposition and Reduction).
The Latin version of that title included two neologisms:
Algebra et Almucabala. The first one stuck.
In fact, al-Khwarizmi describes three different techniques to reduce
equations: al jabr (or transposition from one side of the equation to the other,
mostly to obtain positive quantities only), al muqabala (reduction, or
cancellation of like terms on either side of the equation) and also al hatt
(the division of both sides by the same number).
All such techniques are used jointly and they became
known collectively under the name originally given to the first of them...
By the way, the name "algorithm" comes from al-Khwarizmi's own name
(it was rendered as "Algorismus" in Latin and may otherwise be also transliterated as
"al-Khowarizmi").
So does the rarely used term "algorism" which denotes the decimal system of
numeration, using the so-called "Arabic numerals".
In al-Khwarizmi's own times, these were a fairly recent import from India, and
al-Khwarizmi wrote an elementary text on them, which survives only in its Latin edition
(known to differ substantially from the lost original Arabic version):
Algoritmi de numero Indorum,
which has been translated in English under the questionable title
Al-Khwarizmi on the Hindu Art of Reckoning.
This seminal work seems to be the main reason why modern decimal numerals
are called "Arabic" instead of "Indian".
A footnote about al-Khwarizmi's own name.
He was [apparently] named after his birthplace,
a city whose modern name is Khiva, Khiwa, or Chiwa,
located in modern Uzbekistan, south of the Aral Sea and north of the Caspian Sea
(30 km southwest of Urganch, if you care to look it up).
This walled city is now considered a shrine by the locals.
Its recorded history goes back to the 7th century, but it could be more ancient.
It was once the capital city of Chorasmia
(the country of Kharezm, Khwarazm, or Khorezm),
also known as the Khanate of Khiva from 1511 to 1920
(following conquest by nomadic Uzbeks), straddling modern Uzbekistan and Turkmenistan.
The country was conquered by Russia in 1873 and was known as the
Khorezm Soviet People's Republic from 1920 to 1924...
Because so little is known about al-Khwarizmi's birth, we may wonder if his name
was originally derived from the name of the whole region rather than its capital city,
in which case al-Khwarizmi's exact birthplace would be unknown.
(2004-03-31)
Avoirdupois System (1 av. lb = 1 lb = 0.45359237 kg)
What's the origin of the "avoirdupois" name for units of weight.
Any French-speaking person would instantly recognize this word
as a contraction of the sentence "avoir du poids",
which simply means "to have [a lot of] weight".
The avoirdupois system was originally meant to deal with the measurement of
ponderous goods, as opposed to less bulky things like jewels or
precious metals.
The problem is the spelling.
The French word "poids" is spelled
with a silent "d" not found in the word avoirdupois.
However, this letter was never dropped at all,
since the French changed the spelling of their own word after
the British had borrowed it.
Futhermore, the French did so for a fallacious reason... Read on.
When French spelling was standardized, a few silent letters were
used so that some like-sounding words could be distinguished in writing.
For example, the silent "g" in the word "doigt" (finger)
was borrowed from its Latin etymology (digitus) to distinguish it from
the word "doit" (a form of the verb devoir, which means "must").
Thus, the need to differentiate poids (weight)
and pois (pea) was satisfied by adding a silent "d", ostensibly borrowed
from the Latin word "pondus" (weight).
The funny thing is that the correct etymology of "poids" is
not "pondus" but pensum (massive)
from which the "s" in poi(d)s originates...
So, in a way, it's the French who made the "spelling mistake", not the British.

(D. L. of Manchester.
2000-12-07)
What are the names of the operands in common operations?
- addend + addend = sum (also: term + term = sum)
- minuend - subtrahend = difference
- multiplier ´ multiplicand = product
(also: factor ´ factor = product)
- dividend / divisor = quotient
- base exponent = power
- indexÖradicand = root
With thanks to Steve H. of Edison, NJ (aka bonusspin),
a Math & Physics Junior at Rutgers University (in New Brunswick, NJ),
who appeared on the ABC TV show
Who Wants to Be a Millionaire? on Sept. 14 and Sept. 17, 2000.
Thanks also to Keith McClary
for suggesting multiplier and multiplicand,
whose order may become relevant for noncommutative multiplications,
like the multiplication of matrices (2004-05-24).
Note the consistent use of the suffixes, which are of Latin origin:
-
Dividend= "That which is to be divided"
(the orator Cato ended all of its speeches with
the famous quote "Carthago delenda est": Catharge is to be destroyed).
In a nonmathematical context, dividends are profits that are to be divided among
all shareholders.
-
Divisor = "That which is to do the dividing".
A director does the directing, an advisor
does the advising, etc. In ancient Rome, the Emperor was the
"Imperator", the one supposed to issue the orders (Latin: "Imperare")
A related issue is how native speakers pronounce formulas in English.
Here are the basics:
- x+y : "x plus y".
- x-y : "x minus y".
- x y : "x times y".
- x/y : "x over y".
- If x and y are both integers, y is pronounced as an ordinal:
3/4 = "three fourth".
- xy : "x to the power of y".
- Longer version (elementary level): "x raised to the power of y".
- Shorter version (when x is easy to pronounce): "x to the y".
- If y is an integer, "x to the yth [power]" ("power" is often dropped).
- If y is 2 or 3, "x square[d]" or "x cube[d]" are most common.
There's also the issue of indicating parentheses
and groupings when pronouncing expressions.
If the expression is simple enough,
a parenthesis is adequately pronounced by marking a short pause.
For example, x (y+z) / t could be spoken out
"x times ... y plus z ... over t" (pronouncing "y plus z" very quickly).
When dictating more complex expressions involving parentheses, it's best to indicate
open parent' and close parent', whenever needed.
From a semantical standpoint, the meaning of complex arithmetical expressions
involving elementary operators is the value obtained by applying the operators
in their conventional order of precedence.
Unfortunately, English-speaking schoolchildren are often taught to associate this
with the mnemonic sentence "Please Excuse My Dear Aunt Sally":
Parentheses first,
then Exponentiations, Multiplications, Divisions, Additions and Subtractions...
This should not be blindly relied upon, for the following reasons:
- It tells only part of the whole story.
The other essential part is that you must group things left to right
when encountering operators of the same precedence.
For example, 9-1-2-3 actually means
(((9-1)-2)-3) = 3.
- Addition and subtraction actually have the same precedence so that
9-3+2 is universally understood to mean
(9-3)+2 = 8
(see previous point) and is not equated to the expression
9-(3+2) = 4,
as it would be if addition had higher precedence than subtraction.
- With many computer languages (and/or scientific calculators),
multiplication and division have the
same precedence as well.
This means that 9/3´2
is actually worked out left to right to denote
(9/3)´2 = 6
on many calculators, whereas the written expression
is most likely intended to represent
9/(3´2) = 1½,
according to the rule taught to schoolkids...
Use parentheses to make sure you're understood!
(Monica of Glassboro, NJ.
2001-02-08)
What's the correct terminology for the line
between the numerator and denominator of a fraction?
When the numerator is written directly above the denominator,
the horizontal line between them is called [either a bar or] a vinculum.
(The overbar part of a square-root sign or a guzinta
is also called a vinculum.)
When the numerator and denominator appear at the same level,
separated by a slanted line (e.g., "1/2") such a line is called a solidus
(also virgule or slash).
The related symbol "¸" is called an obelus.
Although this symbol is now virtually unused to separate both parts of a ratio,
it remains very familiar because it is the icon most commonly used to identify the
division key on electronic calculators...
Note:
The name solidus originates from the Roman gold coin of the same name
(the ancestor of the shilling, of the French sol or sou, etc.).
The symbol was originally a monetary symbol, which was still being used for the British
shilling in 1971 (when British money was decimalized).
(2003-11-03) Long Division
Cultural differences in writing the details of a division process.
If you're not a native speaker, you may need to be told that, in English, it's
the same thing to "divide 145 by 5" or to "divide 5 into 145".
How people work out the division 145/5 = 29 depends on where in the World they
learned to do it:
The left layout is used in the US (and the UK, as discussed below).
The right one is apparently dominant elsewhere: France, Brazil, etc.
(There may be others layouts.
Please tell us
how you were taught, where and when.)
Most of the "action" takes place under the dividend (145 in this example).
Either layout is thoroughly confusing to grown-ups who were taught the other way as kids!
On 2004-11-02, Mary
Neerhout Borg (Oregon) asked:[In the US layout]
what is the "little house" over 145 called? |
The order in the English layout (above left) is consistent with the
idiom "5 goes into 145 [29 times]". Therefore, it's been suggested that the symbol
consisting of the top vinculum and the curly vertical part should be
called a guzinta (a tongue-in-cheek name meant to be pronounced like "goes into").
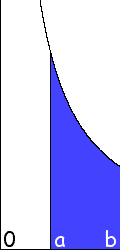
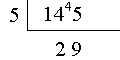 [In a 2004-09-06 e-mail] John
Fannon tells us that, about 1950, young British pupils were instructed
to use the above left layout
[possibly with a straight vertical separation instead of a curly one] only
for long divisions...
For short divisions (with a divisor of 12 or less)
they used another layout, illustrated above,
where the successive remainders appear as superscripts of the dividend's digits...
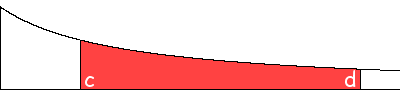
[In a 2004-09-06 e-mail] John
Fannon tells us that, about 1950, young British pupils were instructed
to use the above left layout
[possibly with a straight vertical separation instead of a curly one] only
for long divisions...
For short divisions (with a divisor of 12 or less)
they used another layout, illustrated above,
where the successive remainders appear as superscripts of the dividend's digits...
BigDawn
(2002-02-01)
Is a parallelogram a type of trapezoid?
wazupp
(2002-02-26)
Is a rhombus ever a square?
In a mathematical context, the answer to either question is most definitely yes.
A trapezoid (British English: trapezium) is defined as a quadrilateral
with two parallel sides. If its other two sides happen to be also parallel, the
trapezoid (trapezium) happens to be also a parallelogram. Period.
Common usage may differ from the above because
lexicographers, dictionaries, and the general public often exclude from a general
category some common subcategories.
Mathematicians, however, are much better off considering that
(among many other similar examples):
- an equilateral triangle is an isosceles triangle,
- a circle is an ellipse,
- a square is a rectangle and a rhombus,
- a rectangle is a parallelogram,
- a rhombus is a parallelogram,
- a parallelogram is a trapezoid,
- a trapezoid is a quadrilateral,
- a quadrilateral is a polygon,
- ... etc.
Although you may be able to get away with the opposing view at the most elementary level,
it is poor mathematics to do so.
When the word "trapezoid" is used in actual mathematical discourse, it is universally
understood that any special "subtype" could occur (in the rare cases where it's essential
to have a pair of nonparallel sides, it must be so stated).
Read on, if you're not convinced...
The lexicographers in charge of putting general dictionaries together often
fail to consider the above facts.
Either they copy each other's work, or are content with
the sole monitoring of "common usage", ignoring actual mathematical usage.
Nonmathematical discourse is usually concerned with conveying the most information
in the fewest words about some specific instance of a concept,
so that the word with the narrowest meaning is used whenever possible.
If you're actually looking at some specific circular shape,
you are describing it most accurately as a "circle".
You would not use the term "ellipse" unless the shape failed to be circular...
Mathematical discourse, on the other hand, tries to issue general statements
(theorems)
applicable in the least particular set of circumstances:
If something which is true of circles is true of all other ellipses as well,
it's usually better to state the thing about ellipses in general
(or even conic sections, whenever possible).
Mathematical terms are defined to make
theorems as simple and/or as general as possible.
Nearly anything that is true of an ellipse is also true of a circle, and that is
why mathematicians consider the circle as a special type of ellipse.
In the rare case when a theorem involving ellipses does not apply to circles,
we must say so explicitely.
For example, it's understood that the foci of an ellipse are not necessarily
distinct points...
["Foci", plural of "focus" is pronounced "foe sigh".]
Ultimate argument, for lexicographers:
The meaning of a word is ultimately revealed by its usage.
It stands to reason, then, that lexicographers should find out the meaning of a
mathematical word by analyzing its mathematical usage.
Look at the word "in a sentence" so to speak, rather than put it on a pedestal
and describe whatever prejudices you may have about its meaning.
For the word "trapezoid", you may want to consider a description of
the trapezoid method for approximating integrals:
The definite integral of a positive function f,
is the area bounded by the x-axis, the curve of cartesian equation
y = f(x),
and two "vertical" lines of equations x = a
and x = b (a<b).
For a smooth enough function f, this area is adequately approximated by
using the so-called trapezoid method:
Consider an increasing finite sequence (xn) of points
starting at a and ending at b.
An approximation of the integral of f from a to b
is obtained as the sum (over the relevant range of n) of the areas
of all the trapezoids with vertical bases x = xn
and x = xn+1 whose vertices are either on
the x-axis or on the curve y = f(x).
Now, if f(xn) = f(xn+1), the corresponding
trapezoid happens to be a parallelogram (more precisely,
a rectangle, possibly even a square).
Does this make the above description invalid?
Do you suggest that we should even mention that the
trapezoid could in fact be a rectangle or a square?
Still not convinced about how pervasive inclusive concepts are in regular
mathematical discourse?
Look again at the meaning of other words in the above description of the
trapezoid method.
We talked about an "approximation" to the integral,
but we certainly did not mean to exclude the special case where this
approximation happens to be the exact value, did we?
The approximation is exact when f is linear, but this could
happen in many other cases.
Do you want to even mention such cases?
Also, when f is linear, the "curve" of equation
y = f(x)
is actually a straight line.
Does this bother you?
In the unlikely event that you (or someone you love) could not come to terms with this,
I humbly suggest staying away from any scientific material whatsoever...
Are there exceptions to this rule?
Scientific concepts are as inclusive as they can be, unless a word is used
whose etymology implies exclusion. For example, the term
"pseudoprime" is normally understood
not to apply to a prime number (although definitions and theorems
would be simpler if it did).
We may then clarify things with locutions like
"prime or pseudoprime" for the inclusive concept and "composite pseudoprime"
for the exclusive one (it's better to be pleonastic than misunderstood).
In those cases where there's only one prominent (or "maximal")
special case, the qualifier "proper" may be used:
A proper ellipse is not a circle.
A proper class is not a set.
A proper trapezoid is not a parallelogram.
(L. T. of Austin, TX.
2000-03-30)
What are the names of the polygons 10 sides and up?
(Jason of Canajoharie, NY.
2000-12-06)
What is an 11-sided polygon called?
[What are] the names for polygons with sides numbering 12-20?
(M. Q. of New Port Richey, FL.
2000-11-10)
What are the names of polygons with 11 ,12, 13, 14, ... sides?
(H. I. of Martinsville, VA.
2000-11-30)
What do you call an 11-sided polygon?
(Fred F. of Beverly Hills.
2001-02-10)
What do you call a 13-sided polygon?
(M. K. of Uzbekistan.
2001-02-10)
What is a 32-sided shape called?
An 11-sided polygon is an hendecagon.
Terms like "undecagon" and "duodecagon" have sometimes appeared to denote polygons
with 11 or 12 sides. These are macaronic terms (namely, terms built from a mixture
of different languages, like Greek and Latin) and they should be avoided.
Unfortunately, the term "undecagon" seems to be used almost as often as "hendecagon"
to describe an 11-sided polygon (the very questionable spelling "endecagon" is, mercifully,
a very distant third).
The systematic
naming of polygons is
purely based on Greek roots (we do not call polygons "multigons").
The classification below starts with "polygons" with one or two sides,
which are legitimate topological objects.
Such sides may not be straight lines in euclidean geometry,
but they can be "straight" in noneuclidean geometries:
On the surface of a sphere, the equivalent of a straight line is a great circle
and a monogon or henagon consists of a single vertex and
any great circle going through it,
whereas a digon consists of two vertices and both of the great arcs joining them
(for two antipodal vertices, many digons may be constructed whose edges are
great half-circles).
There's no specific name for the empty polygon, 0-gon (0 vertices, 0 edges),
so the entire sequence is as follows (it's also acceptable to call an "n-gon"
any polygon with n edges):
henagon or monogon (1; almost unused), digon (2; almost unused),
triangle or trigon (3; adjective is "trigonal" or "triangular"),
quadrilateral, quadrangle or tetragon (4; adjective is "tetragonal" or "quadrangular"),
pentagon (5), hexagon (6), heptagon (7; avoid "septagon"), octagon (8),
enneagon (9; avoid "nonagon"),
decagon (10),
hendecagon (11; avoid "undecagon"),
dodecagon (12; avoid "duodecagon"),
triskaidecagon or tridecagon (13),
tetrakaidecagon or tetradecagon (14; avoid "quadridecagon"),
pentakaidecagon or pentadecagon (15; avoid "quindecagon"),
hexakaidecagon or hexadecagon (16),
heptakaidecagon or heptadecagon (17; avoid "septadecagon"),
octakaidecagon or octadecagon (18),
enneakaidecagon or enneadecagon (19; avoid "nonadecagon"),
icosagon (20),
icosikaihenagon or henicosagon (21),
icosikaidigon or docosagon (22),
icosikaitrigon or tricosagon (23),
icosikaitetragon or tetracosagon (24),
icosikaipentagon or pentacosagon (25),
icosikaihexagon or hexacosagon (26),
icosikaiheptagon or heptacosagon (27),
icosikaioctagon or octacosagon (28),
icosikaienneagon or enneacosagon (29; avoid "nonacosagon"),
triacontagon (30), triacontakaihenagon or henitriacontagon (31),
triacontakaidigon or dotriacontagon (32)...
tetracontagon (40)... pentacontagon (50)... hexacontagon (60)... heptacontagon (70)...
octacontagon (80)... enneacontagon (90; avoid "nonacontagon")... hectagon (100), ...
chiliagon (1000), ... myriagon (10 000).
(2001-06-24)
Chemical Nomenclature:
The Greek numerical prefixes are not limited to the naming of polygons; they are the
basis of the systematic naming of other families of scientific objects which depend on
some primary count.
One important example is the
(extended)
official nomenclature for organic molecules,
based on the number of carbon atoms in the backbone of the molecule,
as established in 1957 by the IUPAC
(International Union of Pure and Applied Chemistry).
As is the case with simple polygons, simple organic molecules may have a common name
which was used in various languages before systematic naming was introduced.
Much more so, in fact...
Note that systematic classifications may or may not be extended to start with zero:
Some early chemists did classify water as the simplest
(carbon-free) alcohol.
(Water is about as good a polar solvent as other alcohols.)
However, it's much less useful to view hydrogen as the "simplest alkane".
 It would be a counterproductive, misguided and dubious endeavor
[you've been warned!] to introduce degenerate cycles of
1 or 2 carbon atoms into chemical nomenclature,
but let's have some investigative fun:
Ethylene (C2H4 or H2C=CH2) is in fact
"cycloethane", whereas methylene (CH2 ) is "cyclomethane".
On the other hand, "cycloethanol" would be yet another name for
ethenol (H2C=CHOH), also known as vinyl alcohol or hydroxyethylene.
Finally, "cyclomethanol" would be hydroxymethylene
(HCOH).
It would be a counterproductive, misguided and dubious endeavor
[you've been warned!] to introduce degenerate cycles of
1 or 2 carbon atoms into chemical nomenclature,
but let's have some investigative fun:
Ethylene (C2H4 or H2C=CH2) is in fact
"cycloethane", whereas methylene (CH2 ) is "cyclomethane".
On the other hand, "cycloethanol" would be yet another name for
ethenol (H2C=CHOH), also known as vinyl alcohol or hydroxyethylene.
Finally, "cyclomethanol" would be hydroxymethylene
(HCOH).
| n | Polygon |
Alkane
H(CH2)nH
cyclo: (CH2)n |
p-monoalcohol CnHn+2O
H(CH2)p-1CHOH(CH2)n-pH
Cycloalcohol: (CH2)n-1CHOH |
| 0 | | hydrogen | water |
|---|
| 1 |  henagon henagon
monogon |
methane | methanol (or carbinol) |
|---|
| 2 |  digon digon |
ethane | ethanol |
|---|
| 3 | 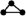 trigon trigon
triangle |
propane
cyclopropane |
1-propanol, 2-propanol
cyclopropanol |
|---|
| 4 | tetragon
quadrangle
quadrilateral |
butane
cyclobutane |
1-butanol, 2-butanol
cyclobutanol |
|---|
| 5 | pentagon | pentane
cyclopentane |
1-pentanol, 2-pentanol, 3-pentanol
cyclopentanol |
|---|
| 6 | hexagon | hexane
cyclohexane |
1-hexanol, 2-hexanol, 3-hexanol
cyclohexanol |
|---|
| 7 | heptagon | heptane
cycloheptane |
1-heptanol, 2-heptanol, 3-heptanol
4-heptanol, cycloheptanol |
|---|
| 8 | octagon | octane
cyclooctane |
1-octanol, 2-octanol, 3-octanol
4-octanol, cyclooctanol |
|---|
| 9 | enneagon | nonane [sic]
cyclononane |
1-nonanol [sic], 2-nonanol, 3-nonanol
4-nonanol, 5-nonanol, cyclononanol |
|---|
| ... etc. |
In 1957, the IUPAC (carelessly) endorsed the use of
the Latin prefix "nona-" for "9" in the names of organic and other chemicals,
and we must now use "nonane" or "nonanol" and refrain from any witty remarks to the
effect that "enneane" or "enneanol" would have been more correct...
Also, "eicosa-" (rather than "icosa-") is the recommended form of the prefix for "20"
in a chemical context.
Many alternate names exist for a large number of important organic chemicals.
For example, the simplest carboxylic acid (methanoic acid, HCOOH) was originally called
formic acid, because it was first distilled (!) from ants
(Latin: formicae, French: fourmis).
Formaldehyde (CH2O, CAS 50-00-00) is thus the common name
of what is more properly called methanal. The French commonly call formaldehyde
formol, with an unfortunate use of a suffix normally reserved for alcohols
(the name formal [sic] has been proposed, which would feature the proper suffix
for an aldehyde, but it never caught on).
Just to take a cheap shot at the practical lack of standardization in some chemical
names, here are some of the published names used for O=CH2,
in alphabetical order:
BFV, CH2O, FA, Fannoform, Floguard 1015, FM 282, Formaldehyde,
Formalin, Formalin 40, Formalith, Formic aldehyde, FYDE,
H2CO, Hoch, Ivalon, Karsan, Lysoform,
Methaldehyde, Methanal, Methyl aldehyde, Methylene glycol, Methylene oxide,
Morbicid, Oxomethane, Oxymethylene, Paraform, Superlysoform,
NCI-C02799, RCRA waste number U122, UN 1198, UN 2209.
Other foreign designations occasionally surface in English
texts, including: "Aldéhyde formique" or "Formol" (French),
"Aldeide formica" or "Formalina" (Italian),
"Aldehyd mravenci" (Czech), "Formaldehyd" (Polish),
"Formaline" (German), or "Oplossingen" (Dutch)...
| n:0 |
Chemical adjectives commonly used for straight counting : |
|---|
| 1:0 | methanoic, methylic, formic, formylic |
|---|
| 2:0 | ethanoic, ethylic, acetic |
|---|
| 3:0 | propanoic, propylic, propionic, ethylformic, metacetonic |
|---|
| 4:0 | butanoic, butyric, propylformic |
|---|
| 5:0 | pentanoic, (also pentyl or amyl), propylacetic,
valeric, valerianic |
|---|
| 6:0 | hexanoic, hexoic, hexylic, pentylformic, pentiformic,
caproic, capronic |
|---|
| 7:0 | heptanoic, heptoic, heptylic, enanthic, oenanthic,
enanthylic, oenanthylic |
|---|
| 8:0 | octanoic, octoic, octylic, octic, caprylic |
|---|
| 9:0 | nonanoic, nonoic, nonylic, pelargic, pelargonic |
|---|
| 10:0 | decanoic, decoic, decylic, capric, caprinic |
|---|
| 11:0 | undecanoic, undecoic, undecylic, hendecanoic |
|---|
| 12:0 | dodecanoic, dodecoic, dodecylic, vulvic,
lauric, laurostearic |
|---|
| 13:0 | tridecanoic, tridecoic, tridecylic |
|---|
| 14:0 | tetradecanoic, tetradecoic, tetradecylic,
myric, myristic |
|---|
| 15:0 | pentadecanoic, pentadecoic, pentadecylic |
|---|
| 16:0 | hexadecanoic, hexadecoic, hexadecylic, cetylic,
palmic, palmitic |
|---|
| 17:0 | heptadecanoic, heptadecoic, heptadecylic, daturic,
margaric, margarinic |
|---|
| 18:0 | octadecanoic, octadecoic, octadecylic, cetylacetic,
steric, stearic |
|---|
| 19:0 | nonadecanoic, nonadecoic, nonadecylic |
|---|
| 20:0 | eicosanoic, icosanoic, arachic, arachidic |
|---|
| 21:0 | heneicosanoic |
|---|
| 22:0 | docosanoic, behenic |
|---|
| 23:0 | tricosanoic |
|---|
| 24:0 | tetracosanoic, lignoceric |
|---|
| 25:0 | pentacosanoic |
|---|
| 26:0 | hexacosanoic, cerinic, cerotic |
|---|
| 27:0 | heptacosanoic, carboceric |
|---|
| 28:0 | octacosanoic, montanic |
|---|
| 29:0 | nonacosanoic |
|---|
| 30:0 | triacontanoic, melissic |
|---|
| 31:0 | hentriacontanoic |
|---|
| 32:0 | dotriacontanoic, lacceroic, lacceric |
|---|
| 33:0 | tritriacontanoic, psyllic, ceromelissic |
|---|
| 34:0 | tetratriacontanoic, geddic, gheddic |
|---|
| 35:0 | pentatriacontanoic, ceroplastic |
|---|
-
The numerical designations n:0, shown above, are commonly used by chemists for a
saturated chain of n carbons (no double bonds). An unsaturated chain of n carbons with
p double bonds would be designated n:p. For example:
Myristoleic is 14:1,
palmitoleic is 16:1,
oleic is 18:1, linoleic is 18:2, linolenic is 18:3,
moroctic is 18:4,
gadoleic is 20:1, arichidonic is 20:4, timnodonic is 20:5,
erucic is 22:1, clupanodonic is 22:5,
selacholeic or nervonic is 24:1,
...
These traditional adjectives for unsaturated carbon chains
usually apply to only one particular position of the
double bond(s) and/or one particular cis/trans configuration.
For other unsaturated carbon chains with the same numerical designations,
it's better to use numerical adjectives based on the two numbers involved
(except if the second one is 1).
The ending to use is "-enoic", as a reminder that an alkene series is involved.
Examples include docosenoic or docosaenoic (22:1,
instead of erucic),
docosadienoic (22:2), docosatrienoic (22:3), docosatetraenoic (22:4)
and docosapentaenoic (22:5, instead of clupanodonic).
The popular (overmarketed) compound DHA does not have a competing traditional
name, it's "simply" called docosahexaenoic acid (22:6).
In the above table for saturated chains,
the official systematic adjectives are given first in each list.
Notice many competing semi-regular formations with a few exceptional cases of their own:
Butyric is used instead of butylic (which is unused in English)
because of the etymological influence of butyrum (butter); the French do use
butylique.
Pentyl and amyl are used as names, but do not
serve as the bases for adjectives.
In a number of cases, systematic adjectives are far less popular than the
traditional ones which
appears in bold face toward the end of some lists.
Such traditional adjectives are usually derived from the names of plants
containing the corresponding unsaturated
fatty acids
(alkanic carboxylic monoacid).
In at least two cases, the etymology is the name of an animal;
a tiny one (the ant) for formic, as discussed above,
and the largest one (the whale) for cetylic :
The adjective cetylic does come from
cetus, the Latin name of the whale (the corresponding alternate name
of hexadecane is cetane, but cetanoic is unused).
The corresponding fatty acid was originally obtained from spermaceti
extracted from the head of the sperm whale or other cetaceans
(spermaceti products were used to make candles, cosmetics, and ointments).
Cetylic acid is better known as palmitic acid (rather than hexadecanoic acid),
as a reminder that it is one of the primary components of palm oil
and coconut oil.
Let's summarize the etymologies of some of the words tabulated above:
Methylic (Greek methu wine and hyle wood; wood alcohol),
formic (Latin formica ant),
ethylic (Latin aether upper air, volatile spirit),
acetic (Latin acetum vinegar),
propionic (Greek pro- first and pion fat; first fatty acid),
butyric (Latin butyrum butter),
amyl (amylum starch, French amidon),
caproic, capronic, capryilic, caprinic, capric
(Latin caper goat; because of the associated smell),
valeric and valerianic (the fatty acid occurs in the root of the valerian plant),
pelargonic (Latin pelargonium, genus name of the geraniums),
lauric (Latin laurus laurel),
myric and myristic (Greek muron perfume, and muristikos fragrant),
cetylic and cetane (Latin cetus whale),
palmic and palmitic (palmite, pith of the palm tree, and palmitin palm oil),
margaric and margarinic (Greek margaron pearl; pearly white aspect of margarin),
stearic (Greek stear tallow, hard fat),
arachic and arachidic (New Latin arachis, genus name of peanuts and groundnuts,
from the Greek arakis legume),
behenic,
lignoceric (wax from beech; Latin lignum wood and cera wax).
Help from our readers:
In an early version of this article,
we had wondered about the etymology of behenic
(wrongly guessing a relation with behemoth).
More than a year after being posted here, our
plea for help
was answered by Valerio Parisi, whom we thank for the following comment about the
kelor tree
(also known as
moringa,
horseradish tree,
dangap in Somalia,
etc.)
In 1848, behenic acid was first reported as a constituent (up to 8.6%) of
the Moringa oleifera seed oil and was subsequently named after
that oil's common designation:
ben oil or behen oil.
On 2002-12-19, Valerio Parisi
wrote: [edited text + hyperlinks]
Dear Dr. Michon,
Here is a loose translation of what my Italian dictionary has to say about
the etymology of "behenic"
(Zingarelli: vocabolario della lingua italiana
- Zanichelli editore; decima edizione, 1970).
Note the spurious coincidence linking the eleventh month of the year
and the eleven pairs of carbon atoms in the behenic chain:
Ben-oil tree (Moringa
oleifera)
Tree of the Moringaceae family, bearing white flowers.
Behen oil
is extracted.from its seeds.
[Italian bèen.
From the Persian bahman: eleventh month of the
Persian year,
corresponding to the sign of Aquarius,
when the roots of this tree were traditionally harvested and consumed.]
|
You may notice that chains with an odd number of carbon atoms have fewer
traditional designations.
The reason is that plants synthesize
fatty acids with an even number of carbons.
In the original version of this article,
we asked any "biologist or organic chemist" for an
explanation of this fact.
About 9 months later, Bruce Blackwell answered the call:
On 2002-04-01, Bruce Blackwell
wrote:
I must say I have enjoyed your Numericana web site thoroughly.
I am a physicist by training but I am self-educated in many sciences,
including organic and biochemistry.
The reason most biological fatty acids have an even number of carbon atoms is
that the predominant mechanism of synthesis in the cell
is the repetitive condensation of acetate
( CH3COO- )
to the growing chain; hence 2 carbons at a time.
The carboxyl end of the growing chain (which begins with a single acetate)
is condensed to the alpha carbon of a new acetate in a reaction similar to a synthesis
in the laboratory known as the Claisen condensation.
In the living cell, the reaction is mediated by enzymes and sulphur atoms.
In the laboratory, Grignard reagents are used.
It has been a pleasure working through the examples on your site.
Bruce Blackwell
Oracle Corporation, Nashua, NH
|
Thanks for the explanation, Bruce. Your kind words are also appreciated...
Lynda Brown
(Canada, 2001-08-21; e-mail.) [ ... about "sesqui" ... ]
I wondered if you happen to know why phosphorus sesquisulfide is
P4S3
where neither element is the "sesqui" of the other. Thanks.
The usual meaning of the "sesqui" prefix is "one and a half ".
A sesquicentury is 150 years and a sesquicentennial marks the passing of this many years.
The only fractional prefixes in common scientific usage are hemi (1/2) and,
indeed, sesqui (3/2).
However, it is acceptable to combine hemi with any prefix representing a
whole number (almost always an odd one).
The most "common" example is hemipenta (5/2).
Although we've never actually encountered prefixes like hemihepta (7/2),
or hemiennea (9/2), these would be allowed to
form [new] scientific names; their meaning is clear and unambiguous...
P4S3
is now called tetraphosphorus trisulphide.
This compound was once an important discovery, with huge social implications
(see below)
around the turn of the 20th century. The curious name of
phosphorus sesquisulphide was apparently given to it at the time by its
French inventors, the chemists Henri Savène and Emile David Cahen
(and/or their entourage).
It may have been just a catchy name, whose use was considered somewhat acceptable
because of the scarcity of fractional prefixes outlined above.
The only other accurate names for the chemical, besides tetraphosphorus trisulphide,
would be diphosphorus sesquisulphide or phosphorus hemisesquisulphide,
which would look even weirder to any modern chemist.
It may well be the case that Savène and Cahen originally used
a "proper" name and that it was shortened later because there is really no
possible risk of confusion!
You were right to observe that all this is not very satisfying and/or logical.
Others found it unsatisfying as well, and this is why the
more precise name of tetraphosphorus trisulphide is now used.
Matches,
Phosphorus, and P4S3
An household match is such a common item nowadays
that it may be hard to imagine what a revolutionary
marvel it once was! Vigorously rubbing two pieces of wood together
may generate enough heat to allow some dry material to smolder and then ignite in the
presence of a spark from metal or silex.
This can be very hard work, as many boy scouts will tell you!
The idea of the match is to carefully choose the materials involved, so that
friction will cause enough heat locally as well as some sparking to trigger ignition of
flammable material...

Surprisingly, some early matches did not include the element now
readily associated with them: phosphorus.
The first practical friction matches were only made in 1826 from
a fifty-fifty mixture of potassium chlorate and antimony trisulphide
(with gum arabic, sugar and starch).
They were called "friction lights" by their inventor, John Walker (1781-1857), an English pharmacist from Stockton-on-Tees
[at 59 High Street]
who did not patent his creation.
These early matches were bulky 3-inch splints of wood, expensive, unreliable, and
somewhat inconvenient to use.
They were first sold on April 7, 1827, to a local solicitor by the name of Hixon.
All this would change in 1831.
Charles
Sauria (1812-1895)
was then a young chemistry student from the French village of Saint-Lothain
(Jura) and he had managed to make the first modern "strike-anywhere" match
(in 1830 or 1831)
by substituting white phosphorus
for the antimony sulfide in the Walker recipe.
The idea was first applied industrially in 1832 by Jakob Friedrich Kammerer;
Sauria himself did not profit from his invention
(he died a pauper).
The white phosphorus "strike-anywhere" matches
became known as Lucifers,
the trademark coined by Samuel Jones in 1829 or 1830 and
originally intended for the previous generation of matches.
The name may have been far more appropriate than it was meant to be:
For one thing, Lucifers could ignite accidentally rather easily
(pure white phosphorus may ignite spontaneously in the air above 34°C).
It was also soon discovered that white phosphorus is highly toxic:
Continuous exposure among factory workers
(impoverished "match girls") would cause a dreaded and often fatal
bone disease known as phossy-jaw.
White phosphorus became a public health issue on the international scene...
The French goverment sponsored research to find a suitable replacement
to white phosphorus.
The outcome, the work of H. Savène and E.D. Cahen,
was based on tetraphosphorus trisulphide, a yellow solid melting at 172°C
(then called phosphorus sesquisulphide, as mentioned above).
A paste including 13% of that chemical and 28% potassium chlorate worked very well
(the rest of the recipe included powdered glass, glue and fillers such as zinc oxide
and iron oxide ).
It was not spontaneously flammable, it was not poisonous,
it did not cause phossy-jaw!
A perfect product with a lousy name.
In 1906, an international treaty (the so-called Berne Convention) was signed
in Switzerland,
obligating the signing countries to ban white phosphorus
from the manufacture of matches.
The US did not sign the Berne Convention (on the grounds that the required
ban would not be constitutional)
but the US Congress created punitive taxes which had the same effect, in 1913.
All this did not prevent toxic Lucifers from being manufactured in China,
as late as 1950...
In the U.S., the patent for P4S3
matches was secured in 1910 by the Diamond Match Company.
However, the public health issue was such that President Taft
publicly urged the company to voluntarily surrender
its patent into the public domain, despite its enormous moneymaking potential.
The Diamond Match Company did so on January 28, 1911.
At this writing,
the nontoxic P4S3 "strike-anywhere" matches
are still very popular in the US.
In many other countries, however, they have been all but replaced by
the so-called safety matches,
which you can only strike on a special patch (normally located outside each package)
coated with some red phosphorus, which is essential to ignition.
This type of safety match was invented
in 1855, by Johan Edvard Lundstrom of Sweden.
The invention was made possible by the previous discovery of red phosphorus,
the nontoxic form of phosphorus (which is obtained by heating ordinary
white phosphorus between 230°C and 300°C in the absence of oxygen).
For other aspects of the whole story, see the wonderful book of John Emsley,
The
13th Element: The Sordid Tale of Murder, Fire and Phosphorus
(John Wiley & Sons, New York, 2000. ISBN 0-471-39455-6).
The title of the book comes from the fact that phosphorus
was discovered around 1669 in Hamburg, by the alchemist Hannig Brandt,
at a time when only 12 other chemical elements were known:
Gold, Silver, Mercury, Copper, Iron, Zinc, Tin, Lead, Antimony, Arsenic, Carbon,
and Sulphur.
On 2001-08-21, Lynda Brown
(Canada) wrote:
Thank you very much for your prompt and detailed answer.
I had not guessed that "hemi" might have been involved,
but that makes perfect sense.
Ironically, I had just finished reading John Emsley's book on phosphorus
(am now reading "Molecules at an Exhibition").
Regards, Lynda Brown
|
References:
(M. P. of Saint Petersburg, FL.
2000-11-04)
If you have a million, billion, and a trillion,
what are the next 5 large numbers that come after that?
Here's the sequence: million (n=1), billion (n=2), trillion (n=3), quadrillion (n=4),
quintillion (n=5), sextillion (n=6), septillion (n=7), octillion (n=8),
nonillion (n=9), decillion (n=10), ... vigintillion (n=20), ... centillion (n=100).
[See table below.]
The n-th word in this sequence may be referred to as the n-th zillion.
This word pattern was devised around 1484 by Nicolas Chuquet (1445-1488),
who authored the first treatise of algebra ever written by a Frenchman.
Chuquet (a self-described "algorist")
used the word for the n-th zillion to denote a million to the n-th power,
namely 106n, where n is as listed above [or tabulated below].
However, things did not remain so simple with the passage of time...
In the 17th century, a few influential French mathematicians decided to use
the same names to denote the successive powers of a thousand instead,
namely 103n+3, where n is as listed above [or tabulated below].
This was described as a "corruption of the Chuquet system"
but was considered more "practical".
That's the system used in the US today (where a billion is indeed 1000 000 000)
and increasingly in English texts of any origin.
In 1974, British Prime Minister Harold Wilson even informed the House of Commons
that the word "billion" in statistics from the British government would
thenceforth mean 109, in conformity with American usage...
However, since the original Chuquet system is still used in the UK,
it's probably best to avoid such names in international communications,
if there is any risk of ambiguity whatsoever.
Astronomers, in particular, routinely speak of a "thousand million"
(legal in the Chuquet system, weird but unambiguous in the American one)
or a "million million" (not legal in either system, but unambiguous in both).
After using the "American system" for quite a while, France reverted back to
the original Chuquet system in 1948 and declared any other system illegal in 1961.
Also in 1948, the 9th CGPM approved the original Chuquet system for international
use in scientific fields.
The trend seems to be that the Chuquet system is used in all languages but English,
where the American system is increasingly dominant (especially in a financial context).
A "billion" in English almost always means 1000 000 000,
the corresponding British term "milliard", which would be unambiguous,
is apparently rarely used nowadays.
Nevertheless, a "zilliard" sequence is being used to denote 103+6n.
These are numbers 1000 times larger
than the corresponding "zillions" of the original Chuquet system, whose gaps
compared with the American system are thus filled:
milliard (109),
billiard [sic!] (1015),
trilliard (1021),
quadrilliard (1027), etc.
| n | nth zillion | US | World |
|---|
| 1 | million |
106 | 106 |
| | milliard |
| 109 |
| 2 | billion |
109 | 1012 |
| 3 | trillion |
1012 | 1018 |
| 4 | quadrillion |
1015 | 1024 |
| 5 | quintillion |
1018 | 1030 |
| 6 | sextillion |
1021 | 1036 |
| 7 | septillion |
1024 | 1042 |
| 8 | octillion |
1027 | 1048 |
| 9 | nonillion |
1030 | 1054 |
| 10 | decillion | 1033 | 1060 |
| 11 | undecillion | 1036 | 1066 |
| 12 | dodecillion
duodecillion | 1039 | 1072 |
| 13 | tredecillion | 1042 | 1078 |
| 14 | quattuordecillion | 1045 | 1084 |
| 15 | quindecillion | 1048 | 1090 |
| 16 | sexdecillion | 1051 | 1096 |
| 17 | septendecillion | 1054 | 10102 |
| 18 | octodecillion | 1057 | 10108 |
| 19 | novemdecillion | 1060 | 10114 |
| 20 | vigintillion | 1063 | 10120 |
| n | nth zillion | US | World |
|---|
| 21 | unvigintillion | 1066 | 10126 |
| 22 | dovigintillion
duovigintillion | 1069 | 10132 |
| 23 | trevigintillion | 1072 | 10138 |
| 24 | quattuorvigintillion |
1075 | 10144 |
| 25 | quinvigintillion | 1078 | 10150 |
| 26 | sexvigintillion | 1081 | 10156 |
| 27 | septenvigintillion |
1084 | 10162 |
| 28 | octovigintillion | 1087 | 10168 |
| 29 | novemvigintillion | 1090 | 10174 |
| 30 | trigintillion | 1093 | 10180 |
| 31 | untrigintillion | 1096 | 10186 |
| 32 | dotrigintillion
duotrigintillion | 1099 | 10192 |
| 33 | tretrigintillion | 10102 | 10198 |
 |
| 40 | quadragintillion | 10123 | 10240 |
| 50 | quinquagintillion |
10153 | 10300 |
| 60 | sexagintillion | 10183 | 10360 |
| 70 | septuagintillion | 10213 | 10420 |
| 80 | octogintillion | 10243 | 10480 |
| 90 | nonagintillion | 10273 | 10540 |
| 100 | centillion | 10303 | 10600 |
Note:
The American system is also used in Russian, except that "milliard" is used instead of
"billion" (which is apparently a rarely used synonym).
There seems to be a few
other exceptions, though.
If you are absolutely certain about any language and/or country in which
the American system is used, please
let us know.
The only (unconfirmed) such "exceptions" we have gleaned so far are
Turkish, Greek and Romanian,
as well as
Spanish in Puerto Rico (or in the U.S.),
and
Portuguese in Brazil.
(Mark of Edmond, OK.
2000-11-06)
What is the name of the number represented by 100 000 to the power of 100 000
(a 1 with 1/2 million zeros)?
Following Rudy Rucker (quoted by John Conway and Richard Guy on the subject), we may use
the suffix plex at the end of a number to denote 10 to the power of
that number: zeroplex is 1, oneplex is 10, twoplex is 100, threeplex is 1000, etc.
The celebrated googol is a hundredplex (which exceeds by far the total number of
elementary particles in the Universe)...
The neologism "googol" was coined in 1938 by the American mathematician Edward Kasner
(1878-1955) who was looking for a cute term to stand for 10 to the 100th.
The standard names for this number would be "ten dotrigintillion" or "ten duotrigintillion"
in the American system of numeration (where a billion is a thousand million)
and "ten thousand sexdecillion" in the original Chuquet system of numeration
(still used by a few British subjects, and by virtually the entire
non-English-speaking world, who considers that a billion is a million million).
Kasner asked for the opinion of his nine-year-old nephew (Milton Sirotta) who came up
with "googol". The name stuck.
A googolplex is 1010100, a number which is
impossible to write down with ordinary numeration, since this would entail the digit "1"
followed by a googol of zeroes. (The suffix plex is a contraction of
"plus exponent". The suffix minex has been proposed by
Tadashi Tokieda as a contraction
of "minus exponent" to denote small numbers: zerominex is 1, oneminex is 1/10,
twominex is 1/100, etc.)
One answer to your question would therefore be that 100000100000
may be called"500000-plex".
This is allowed, but you may argue that the use of numerals does not
make this more of a "name" than
100000100000 or 10500000.
The problem is that the plex suffix leads to ambiguity when used with number names
that consist of several words:
Does "five hundred thousandplex" mean 500000plex or 500 times a 1000-plex?
To solve the problem almost unambiguously in this particular case,
we need a single word to represent 500000...
There happens to be a legitimate one, using the standard prefix hemi- for "one half":
500000 is a hemimillion and your number could therefore be called a
hemimillionplex .
That is a correct answer unless you make a different parsing and consider that a
"hemimillionplex" is a "hemi[millionplex]" instead of a "[hemimillion]plex" as intended.
I argue that this should not be done on the basis that the former parsing is less
"useful" than the latter, since it would put large numbers with short names
"too close" to each other and leave more severe gaps in-between.
In other words, the hemi- prefix (like the other standard numerical prefixes
sesqui-, di-, tri-, quadra-, penta-, etc.)
should have a stronger parsing priority than the suffix plex.
An hyphen (hemimillion-plex) would probably make
the whole thing less ambiguous, but this breaks the pattern established for lesser numbers.
I don't know what a professional linguist would have to say about all this,
if you happen to be one, please let me know.
Did I really say "useful" ?
On 2003-03-22, Betsy
McCall wrote: [edited summary]
I really like your site, and I decided to weigh in on your linguistic problem.
I study mathematical linguistics (the mathematics of language,
not the linguistics of mathematics, but close enough).
[...]
You are basically correct.
You've obviously considered this problem carefully,
and have tried to follow the normal numerical usage of the prefixes.
[...]
In the end, only usage can determine the "correct" parsing,
but I don't really envision hemimillionplex
becoming popular enough to set a trend.
Another alternative would be to cast 500 000 [purely] in Greek terms
[to obtain] pentacontamyriaplex.
The Greek prefixes will naturally parse together,
though that does mess up the plexing pattern in other ways.
[...]
I seriously doubt that the Oxford English Dictionary
will be quoting any of these words any time soon.
|
|
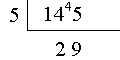 [In a 2004-09-06 e-mail]
[In a 2004-09-06 e-mail] 