Recreational Mathematics
bobbejones
(2001-04-12)
You have 12 marbles, one of them is either heavier or lighter than the rest.
In three weighs on a balance scale, you must determine which is the odd marble.
How do you do this?
This one's a great classic, known as the Counterfeit Coin Problem.
The solution tabulated below is discussed on
another page...
It's also possible to detect an odd marble among 13.
If we are given an extra marble known to be standard, detection among
as many as 14 other marbles becomes possible.
The weighing procedure for 12 marbles: ABCDEFGHIJKL.
| First Weighing |
Second Weighing |
Third Weighing |
| ABCD = EFGH |
AI = JK |
A = L is not possible.
A < L Þ L is heavy.
A > L Þ L is light. |
| AI < JK |
J = K Þ I is light.
J < K Þ K is heavy.
J > K Þ J is heavy. |
| AI > JK |
J = K Þ I is heavy.
J < K Þ J is light.
J > K Þ K is light. |
 |
| ABCD > EFGH |
ABE = CFL |
G = H Þ D is heavy.
G < H Þ G is light.
G > H Þ H is light. |
| ABE < CFL |
C = L Þ E is light.
C < L is not possible.
C > L Þ C is heavy. |
| ABE > CFL |
A = B Þ F is light.
A < B Þ B is heavy.
A > B Þ A is heavy. |
|
| ABCD < EFGH |
ABE = CFL |
G = H Þ D is light.
G < H Þ H is heavy.
G > H Þ G is heavy. |
| ABE < CFL |
A = B Þ F is heavy.
A < B Þ A is light.
A > B Þ B is light. |
| ABE > CFL |
C = L Þ E is heavy.
C < L Þ C is light.
C > L is not possible.
|
(2001-08-20) General Counterfeit Penny Problem
How do you find a single counterfeit coin [either heavier or lighter than
a good one] among n coins in only k weighings on a two-pan balance?
We may imagine that all the information gathered at any point of the
weighing procedure is recorded by putting all the coins in one of four bins
labeled E, G, L, or H (if E is not empty, H and L are):
- E contains e unweighed coins which could be good, heavy, or light.
- G contains g coins known to be good pennies.
- H contains the h coins which are known to be either good or heavy.
- L contains the m coins which are known to be either good or light.
The details of the entire process are presented in our
unabridged discussion.
In k weighings, we may find a counterfeit coin among n coins,
provided n does not exceed the following maximum values:
- ½ (3k-3) to find out if the counterfeit is heavy or light.
- ½ (3k-1) if mere identification suffices, or if we are
given an extra good coin to determine if the counterfeit is heavy or light.
- ½ (3k+1) for mere identification, with an extra coin.
kalisditz
(2001-03-29)
[problem
from Prof. Doug Brumbaugh,
UCF]
In a "seven-eleven" (7-11) store, a customer selected four items to buy.
The check-out clerk says that he multiplied the costs of the items and
obtained exactly 7.11, the very name of the store!
The customer calmly tells the clerk that the costs of the items should be added,
not multiplied.
The clerk then informs the customer that the correct total is also $7.11.
What are the exact costs of the 4 items?
There's only one possible solution, namely:
7.11 = 3.16 + 1.25 + 1.50 + 1.20 =
3.16 ´ 1.25 ´ 1.50 ´ 1.20
Proof :
If a, b, c, d are the prices of the items expressed in (whole) cents,
what we are told is that a+b+c+d = 711 and
abcd = 711000000 = 26 32 56 79.
So, one (and only one) of the amounts, say a, is a multiple of 79.
This is, of course, less than 9 times 79 (which is 711),
and may thus only be 1,2,3,4,5,6, or 8 times 79 (7 times 79 is ruled out,
because it does not divide 711000000).
These 7 possibilities translate into the following equations:
- a=79, b+c+d=632, bcd=9000000
- a=158, b+c+d=553, bcd=4500000
- a=237, b+c+d=474, bcd=3000000
- a=316, b+c+d=395, bcd=2250000
- a=395, b+c+d=316, bcd=1800000
- a=474, b+c+d=237, bcd=1500000
- a=632, b+c+d=79, bcd=1125000
Now, the product of 3 positive numbers of given sum is greatest when they are all equal,
which means that the product bcd cannot exceed (b+c+d)3/27.
This rules out the last three of the above 7 cases.
In the first three cases, on the other hand, the sum b+c+d isn't a multiple of 5,
so at least one of b,c,d (say d) isn't either.
Therefore, the product bc must be a multiple of the sixth power of 5.
Since neither b nor c can be large enough to be a multiple of the fourth power
[625 is clearly too big a share of 711, leaving only 7 cents for two items in the
first case and nothing at all in the other two] we must conclude that
both b and c are nonzrero multiples of 125.
The number d would thus be obtained by subtracting from one of three possible sums
(632, 553, 474) some multiple of 125
(necessarily: 250, 375 or [in the first two cases] 500).
This gives only 8 possible values for d
(382, 257, 132, 303, 178, 53, 224, 99).
Each is unacceptable because it has a prime factor other than 2 or 3.
Therefore, only the fourth case is not ruled out, so that a=$3.16.
a=316, b+c+d=395, bcd=2250000.
Since the sum b+c+d is a multiple of 5, and at least one of the terms is a multiple of 5,
either only one is, or all are.
The former option is ruled out since this would imply for the single multiple of 5
to be a multiple of 56=15625,
which would, by itself, be much larger than the entire sum of 395.
So, b, c, and d are all multiples of 5, and
we may let b=5b', c=5c', d=5d', where b'+c'+d'=79 and b'c'd'=18000.
Now, these three new variables may not be all divisible by 5
(otherwise their sum would be too).
It's not possible either to have a single one of them divisible by 5,
because it would then have to be a multiple of 53=125
and exceed the whole sum of 79.
Therefore, we must have a multiple of 25 (say b'=25b") and a multiple of 5 (say c'=5c"):
25b"+5c"+d'=79 and b"c"d'=144.
It is then clear that b" can only be 1 or 2.
If b" was 2, then we would have 5c"+d'=29 and c"d'=72,
implying that c" is a solution of
x(29-5x)=72 or 5x2-29x+72=0.
However, this quadratic equation does not have any real solutions,
because its discriminant is negative.
Therefore, b" is equal to 1 and b=5(25b")=125=$1.25.
The whole thing thus boils down to solving 5c"+d'=54 and c"d'=144,
which means that c" is solution of
x(54-5x)=144 or 5x2-54x+144=0.
Of the two solutions of this quadratic equation (x=6 and x=4.8),
we may only keep the one which is an integer.
Therefore c"=6, c'=30, c=150=$1.50.
Finally, d'=144/c=24 which means d=5d'=120=$1.20.
Therefore, the solution is unique (the order of the 4 items being irrelevant):
$3.16, $1.25, $1.50, $1.20.
Nice brain teaser... 
Related Puzzles:
13 checkout totals are both the sum
and the product of the prices of two items:
$4.00=2.00+ 2.00 $4.05=1.80+ 2.25 $4.50=1.50+ 3.00
$4.90=1.40+ 3.50 $6.25=1.25+ 5.00 $7.20=1.20+ 6.00
$8.41=1.16+ 7.25 $12.10=1.10+11.00 $14.58=1.08+13.50
$22.05=1.05+ 21.00 $27.04=1.04+26.00 $52.02=1.02+51.00
$102.01=1.01+101.00
There are many amounts which are both the sum and the product of three prices
(7.11 is not one of them), the smallest is 5.25, which is both the sum and the
product of 1.50, 1.75 and 2.00.
The smallest amount for which this happens in two different ways
is 6.6 (either 0.8+2.5+3.3 or 1.1+1.5+4.0).
6.44 (= 1.84+1.75+1.60+1.25) is the smallest amount that's both sum and product
of 4 prices (like 7.11). Next is:
6.51 = 2.00+1.86+1.40+1.25
jsheidy (2001-04-30)
Find the Fallacy
How to prove a right angle congruent to an obtuse angle?
-
Warning: False proof ahead.
An obtuse angle is certainly not congruent to a right angle.
Can you find the well-hidden fallacy?
Maybe you should not trust what you see!
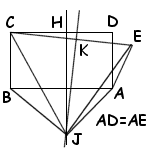
Consider the above picture:
ABCD is a rectangle and E is a point near D slightly outside the rectangle so that
AE is equal to AD. H is the middle of CD and K is the middle of CE.
The perpendicular to CD going through H and the perpendicular to CE going though K
intersect at a certain point J.
Now consider the sides of the triangles BCJ and AEJ:
First, BC=AE (since both of these are equal to AD).
Second, JB=JA (J is on the perpendicular bisector of CD, which is also that of AB).
Third, CJ=EJ (J is on the perpendicular bisector of CE, by construction).
The inescapable conclusion (I swear it's true!) is that BCJ and AEJ are congruent
triangles (as their 3 sides are congruent), therefore the angles CBJ and EAJ are
equal...
The angles JBA and
JAB are equal (since JAB is an isosceles triangle), the picture clearly tells you
that if you subtract JBA from CBJ and
and JAB from JAE you obtain ABC and BAE. Yet one of these (ABC) is a right angle,
whereas the other (BAE) is obtuse by construction. How can this be?
HINT: Every statement is true,
but there are misleading words in the last paragraph.
Only as a last resort,
click here for the solution.
The American mathematician Paul R. Halmos (born in Budapest on
March 3, 1916) rightly said: "You are allowed to lie a little,
but you should never mislead".
Here, the challenge is to find a misleading statement which is not a lie...
Are All Triangles Isosceles?
(2002-01-22)
Accounting Fallacy
Is a raise of $300 twice a year really better than a $1000 annual raise?
-
Warning: The following argument is as fallacious as the previous one.
However, this one has been taken seriously by many people
who should have known better.
This includes columnist Marilyn vos Savant who was once
ridiculed
about this, by one colleague of hers,
among others.
The false argument is that if you get a $300 raise twice a year, what you receive over
and above your initial salary for each successive period of six months seems
to be: $0, $300, $600, $900, $1200, $1500 etc. whereas the corresponding sequence
for successive semesters with a $1000 annual raise is clearly:
$0, $0, $500, $500, $1000, $1000, etc. which is always less.
Pause before reading the next paragraph to see if you can discover the fallacy
by yourself...
The fallacy is, of course, that a $300 raise on your annual salary
(no matter how often you get such a raise) means that you receive
$150 more for each 6-month period, so that the correct sequence if you get a $300 raise
twice a year is $0, $150, $300, $450, $600, $750, etc.
If you're paid weekly, this becomes
worse than the $1000 annual raise in the middle of the fifth month of the second year.
If you were to receive $300 more each semester,
this would properly be called a $600 yearly raise each time you get it (namely twice a year).
This is clearly better than a $1200 yearly raise (you get $300 more in the second semester
of each year),
so there is no paradox in "discovering" that this is more than a $1000 yearly raise.
There are ways to pose the question so that the "paradoxical" answer is the correct one,
but the whole thing may then become an exercise in lateral thinking
(a so-called "trick question") which has little to do with mathematics,
and gives even recreational mathematics a bad name.
It ain't so much the things we don't know that get us in trouble.
It's the things that we know that ain't so.
|
tvbdude
(2002-05-28)
3 men go into a motel.
The receptionist tells them the room will be $30.
Each man pays $10 before going to the room.
The clerk then realizes that they were given only a $25 room,
and sends the bellhop to the room with $5.
The bellhop keeps $2 [as a tip?] and each man gets $1 back,
ending up paying only $9 for the room.
Three times $9 is $27.
With the $2 the bellhop kept, that's only $29.
Where's the missing dollar?
Answer.
(James of Zapata, TX. 2000-10-09)
An island is inhabited by 45 chameleons of 3
varieties: 13 are blue, 15 green, and 17 purple.
Two chameleons of different colors (blue and green, say)
change to the third color (purple) if they meet.
Can they all end up of the same color?
-
Answer.
Diane302 (2002-04-03)
In the old "15 puzzle", you have a square grid (4 by 4) with 15 tiles on it,
numbered 1 through 15.
They're in disarray, and you have to put them in
order by sliding the tiles into the one empty space on the board. [...]
I know that you can place the tiles on the board in either one of two configurations;
one can be put back into the proper order, the other one can't...
How do you determine whether the puzzle can be solved from a given position?
-
The picture shows Sam Loyd's original "14-15 puzzle"
(notice that 14 and 15 have been switched) which once stirred a national craze.
Loyd offered a prize of $1000 for a solution, knowing full well that there was none!
In fact, if you switch any pair of tiles (by lifting them illegally off the board),
there's no way to revert the change with legal moves.
The same thing applies, if you make any odd number of such [illegal] switches.
Something is involved which is called the signature of the permutation:
A permutation of n objects may always be obtained by a sequence of elementary switches.
While there are many different ways to do so, all of them share the
same parity [odd or even] for the number of switches involved.
This parity is the same as that of the number M of so-called
inversions in the permutation.
(An inversion is a pair (A,B) where the number A is less than B,
but comes after B in the permutation.)
Now, consider the number M of inversions in your current position
and let N be the number of the row where the empty space is located
[you may decide that row 1 is at the top and row 4 is at the bottom,
but the only thing that matters is that adjoining rows have different parities].
It's fairly easy to see that the parity of N+M does not change in any legal move:
For an horizontal slide, both M and N are unchanged, whereas both parities do
change in a vertical slide, so that the parity of the sum remains the same
in that case as well
(that's because any vertical slide always switches the relative positions of exactly
3 pairs of numbers, all involving the moving tile).
Therefore, all you have to do is compute this parity for you current position and for your
target position.
If the two do not match,
then the above shows that there is no legal way to go from one position to the other.
Conversely, it so happens that the puzzle can always be solved
when the parities do match (but that's somewhat more difficult to prove).
In technical jargon, the 15-puzzle is said to have two orbits;
it's always possible to travel between two positions within the same orbit,
but you can't jump from one orbit to the other.
ZWEAV
(2001-03-14)
There are five houses in a row on one side of a street.
Each house has its own unique color.
All house owners are of different nationalities.
They all have different pets.
They all drink different drinks.
They all smoke different cigarettes.
[ See the 15 additional numbered statements in the next version of this question. ]
So, who owns the Zebra?
stevehi (Steven Hills
2001-05-26)
Albert Einstein [allegedly] wrote this riddle early on in his career.
He said that 98% of the world's population would not be able to solve it
(there are no tricks, just pure logic).
The question is: Who owns the fish? Here's the riddle:
In a street, there are five houses, painted five different colors.
In each house live a person of different nationality.
The five homeowners each drink a different kind of beverage,
smoke a different brand of cigarette and keep a different pet.
- The Brit [Englishman] lives in the red house.
- The Swede has a dog.
- The Dane drinks tea.
- The green house is on the left of the white house.
- The owner of the green house drinks coffee.
- The person who smokes Pall Mall has birds.
- In the yellow house, they smoke Dunhill.
- The man living in the middle house drinks milk.
- The Norwegian lives in the first house.
- The man who smokes Blend lives next to the house with cats.
- The horseman lives next to the man who smokes Dunhill.
- The man who smokes Blue Master drinks beer.
- The German smokes Prince.
- The Norwegian lives next door to the blue house.
- The man who smokes Blend has a neighbor who drinks water.
-
To avoid nitpicking objections, we first point out
that the question "Who owns the fish?" [or "zebra"]
contains the linguistic presupposition that someone owns it...
The question is not whether someone does but who does. (Isn't it?)
The owner of the fifth pet (i.e., the fish or the zebra)
is German, lives in the green house,
drinks coffee and smokes Prince cigarettes.
If the houses are numbered from left to right,
the green house is number 4 (otherwise it's number 5, as will be shown later).
Also, the young Einstein couldn't possibly have authored the puzzle
in this particular form. Read on.
| 1 | 2 |
3 | 4 | 5 |
|---|
| Color | Yellow | Blue | Red | Green | White |
|---|
| Country | Norwegian | Dane | Brit | German |
Swede |
|---|
| Drink | Water | Tea | Milk | Coffee | Beer |
|---|
| Smoke | Dunhill | Blend | Pall Mall | Prince |
Blue Master |
|---|
| Pet(s) | Cat | Horse | Birds |
Fish | Dog |
|---|
Leftmost-first solution
To obtain the above solution, just start with a blank 5 by 5 table with the leftmost-first
numbering on the top line (we'll deal with rightmost-first ordering later),
then go through all the 15 statements in the order given below,
which allows you to fill all the squares you're told about
(and the fifth square of any line whose other entries have
all been filled):
First, use 8 (Milk=3), 9 (Norwegian=1), 14 (Blue=2), 4 & 5 jointly, 1 and 7...
Statement 3 then places Dane and Tea either at #2 or at #5. It must be #2
(as pictured below), because #5 is easily ruled out with statements 12 and 15.
| |
| 1 | 2 |
3 | 4 | 5 |
|---|
| Color | Yellow | Blue | Red | Green | White |
|---|
| Country | Norwegian | Dane |
Brit | | |
|---|
| Drink | | Tea |
Milk | Coffee | |
|---|
| Smoke | Dunhill | | | |
|
|---|
| Pet(s) | | | | |
|
|---|
| |
However, the same result may be obtained without the convenient help of
statement 15 (we'll see that 15 is actually useless here)
by observing that placing Dane and Tea in column #5 leads to a contradiction,
using 12, 11, 2, and 13, in that order...
Now, you may use statement 12 to place Beer and Blue Master at #5,
which implies that the last drink (Water, according to statement 15) is at #1.
Statement 13, then, puts German and Prince at #4 and Swede at #5.
It's easy to complete the puzzle using statements 2, 11, 6 and 10, in that
order. (Statement
15 has not been used at all,
except to specify that the "fifth drink" is water !)
If statement 9 had been "the Norwegian lives in the leftmost house", this would be the end
of it!
Unfortunately, we also have to deal with the possibility that the "first" house
is, in fact, the rightmost one (a sizeable part of the world population does write
right-to-left).
Just duplicate the above effort with a backward sequence of numbers in the
first line of your table:
| 5 | 4 |
3 | 2 | 1 |
|---|
| Color | Green | White | Red | Blue | Yellow |
|---|
| Country | German | Swede | Brit | Dane |
Norwegian |
|---|
| Drink | Coffee | Beer | Milk | Tea | Water |
|---|
| Smoke | Prince | Blue Master | Pall Mall | Blend |
Dunhill |
|---|
| Pet(s) | Fish | Dog | Birds |
Horse | Cat |
|---|
Rightmost-first solution
With rightmost-first numbering,
you'll find that the exact same sequence works to give the same solution as before,
except that the addresses of the green and white houses (4 and 5) are interchanged
(5 and 4).
It turns out that there is another branch which occurs with a possible choice at the step
involving statements 4 and 5 (alternate choice is green=4 and white=3).
In this case, using the statements in the following order (after 8, 9, 14, 4 and 5):
1, 7, 3, 12, 15, 13, you reach two possibilities that are both shown to be dead ends
(using 2 and 6).
In other words, the solution is unique for each of the two possible left/right
numbering conventions and these two solutions are trivially related by exchanging only
addresses 4 and 5.
You may want to notice that the young Albert Einstein (1879-1955)
couldn't have authored the puzzle in this form:
The Pall Mall brand was introduced by Butler & Butler
in 1899 (sold to American Tobacco in 1907 and Brown & Williamson in 1994)
and Alfred Dunhill was established in 1893 (starting to make pipes in 1907)
when Einstein was still a young man.
However, the Blue Master brand was introduced by J. L. Tiedemann in 1937,
when Einstein was 58!
Such brain teasers could often be found in the publications listed below...
This particular puzzle may well have originated in one of these, and would
owe its enduring popularity to its apocryphal attribution to Einstein:
Chris Cole, the rec.puzzle archivist,
is actively researching this.
Help
him out, if you can.
Logica (French monthly),
Dell Crosswords,
Logic Problems (British),
McCall's Magazine (1950's ?),
PM (German),
The Saturday Evening Post,
Collier's Magazine,
etc.
(L. S. of Canada.
2000-11-21)
To number a book from 1 up to its last page took 552 digits.
How many pages are there in the book?
-
If P(n) is the number of digits used to number n pages, the formula for P(n) is:
- P(n) = n , if n is between 1 and 9
- P(n) = 2n-9 , if n is between 10 and 99
- P(n) = 3n-108 , if n is between 100 and 999
- P(n) = 4n-1107 , if n is between 1000 and 9999
- P(n) = kn-[ (10k -1)/9 - k ] , if n is a k-digit number.
For the question at hand, we simply have to solve the equation 552=(3n-108)
and that means that there are n=220 pages in the book.
 (2002-02-09) [abridged]
Two ferry boats start at the same instant on opposite sides of the river.
One is faster than the other. They cross at a point 720 yards from the left shore on
their way to their respective destinations, where each one spends 10 minutes to change
passengers before the return trip. They meet again at a point 400 yards from
the right shore.
How wide is the river?
-
Before we give
Sam
Loyd's ingenious solution (below),
let's apply what Loyd (wrongly) calls the "cut-and-dried rules of mathematics".
First, we may remark that the time spent by the boats at their destination is irrelevant,
as long as they both spend the same amount of idle time between each encounter.
Ignore it...
[We'll criticize Loyd's solution
later, with an overlooked solution for which
the assumption behind this simplification happens to be false.]
Let u and v be the speeds of the boats and w the width of the river.
Let a = 720 yd
and b = 400 yd be the
distances from the left and right shores given in the
question. What we are told about the crossing points means that:
| a / u | = | (w-a) / v |
| (w+b) / u | = | (2w-b) / v |
Divide each side of the first equality by the corresponding side of the second equality
and you obtain an equality where the speeds of the boats no longer appear,
namely a/(w+b) = (w-a)/(2w-b), or rather
a(2w-b) = (w-a)(w+b), which boils down to
w = 3a-b
(after ruling out w = 0 and dividing by w).
The width of the river is therefore 3a-b = 1760 yd,
or exactly 1 mile.
This answers the question posed, but we may also be curious about the speeds of the
respective boats.
The data given only allows to find their ratio. Plug the value of w = 1760 yd
into either of the above equations to find that u/v = 9/13:
The speeds are in a 13 to 9 ratio and the faster boat started from the right shore.
The above solution follows what Sam Loyd calls the "cut-and-dried rules of mathematics".
He did not think this particular problem should be attacked this way and even ventured
the extreme opinion that
"99% of our shrewdest businessmen would fail to solve it in a week" [sic!].
Well, it's certainly not so, although Loyd does present a simple solution to this particular
problem, which does not require anything beyond common sense and elementary arithmetic
[abridged]:
The first time the boats meet, they have travelled a combined length equal to the
width of the river. The second time, they have travelled a combined length equal
to three times the river's width.
The boat which had travelled 720 yd at the first meeting has
therefore travelled three times that (2160 yd) at the second meeting.
As this boat has then travelled the width of the river plus 400 yd, the river is
thus shown to be 1760 yd wide.
Well, this is indeed an ingenious way to present the solution, but we'd rather use the
"cut-and-dried rules of mathematics" to discover the solution to all
similar problems.
No ingenuity is required to solve these and,
in most cases, ingenuity does not even help much.
Finally, note that the wording of the above question (like Sam Loyd's original wording)
allows another situation, where the slower boat is so slow that it will not even have
completed its first crossing when the returning faster boat overtakes it
(although that faster boat has been delayed t = 10 minutes at shore).
In that case, the width w of the river also depends on another distance d, which is
defined as the product of the delay t by the speed of the faster boat.
If we were given enough data to compute d,
the width w would then be obtained as the positive root of the quadratic equation:
w 2 + (d+b-a) w - a (d+2b) = 0
A fast
modern ferry may
have a speed of about 20 yd/s, which means about 35.549 knots
and would correspond to d = 12000 yd.
Under good conditions the speed could be around 40 knots and we may take
d = 13260 yd (exactly 22.1 yd/s, or about 39.28 knots)
which has the advantage of making
the above quadratic equation solvable in integers (other possible choices with the same
property and a similar magnitude are 10375, 10856, 14862 and 16864).
Under this assumption, the river is seen to have a width w = 740 yd
(the alternate choices for d quoted above give respectively 745, 744, 738 and 736 yards).
Needless to say that there is no "ingenious" shortcut to reach that result.
So much for the case of Sam Loyd against the "cut-and-dried rules of mathematics".
The speed of the slower boat is (w/a-1) times the speed of the faster one.
With our arbitrary choice for d, which gives w = 740,
this means that the slower boat is exactly 36 times slower
than the faster one; moving at the speed of a sluggish rowboat
(about 1.09 knots, 0.614 yd/s, 0.56 m/s,
2.02 km/h or 1.26 mph).
(Gérard Michon.
2000-10-10)
876+429 = 1305 is one way to write a sum which uses all digits (0-9) only once.
How many different ways are there to do this?
-
The answer, which I worked out after posting the question, is 48.
Listed below are the basic 6 pairs of solutions.
Each of these represents 4 distinct solutions obtained by switching digits between the
two summands.
(We count as distinct only different pairs of summands,
not the same pair in a different order.)
879+426 = 1305 & 879+624 = 1503
859+347 = 1206 & 859+743 = 1602
789+264 = 1053 & 789+246 = 1035
756+342 = 1098 & 765+324 = 1089
657+432 = 1089 & 675+423 = 1098
589+473 = 1062 & 589+437 = 1026
The same question may be asked for products.
There are only 22 solutions:
58401 = 63´927 32890 = 46´715 26910 = 78´345
19084 = 52´367 17820 = 36´495 & 17820 = 45´396
16038 = 27´594 & 16038 = 54´297 15678 = 39´402
65821 = 7´9403 65128 = 7´9304 34902 = 6´5817
36508 = 4´9127 28651 = 7´4093 28156 = 4´7039
27504 = 3´9168 24507 = 3´8169 21658 = 7´3094
20754 = 3´6918 20457 = 3´6819 17082 = 3´5694
15628 = 4´3907
(B. O. of Schenectady, NY.
2001-02-07)
[...] The four members of U2 (Bono, Edge, Adam, and Larry) must cross a bridge
in 17 minutes in order to get to their concert on time.
The conditions: 2 people can cross at a time and they walk at the slower person's
rate when crossing (Bono - 1 min to cross, Edge - 2 minutes, Adam - 5 minutes,
Larry - 10 minutes).
They must travel with the one flashlight when crossing.
How can everyone get across within 17 minutes?
-
- B and E cross in 2 minutes and B comes back with the flashlight in 1 minute
(leaving E on the other side). Total: 3 minutes.
- A and L cross in 10 minutes and E comes back with the flashlight in 2 minutes.
Total: 12 minutes.
- Finally, B and E cross in 2 minutes, for a grand total of 17 minutes.
Note: Another solution is to have E (instead of B) come back with the
flashlight in the first step, which would then take 4 minutes (instead of 3):
In the second step, B would bring back the flashlight and it would only take 11 minutes
(instead of 12) for the same grand total of 17 minutes.
(Susan of Modesto, CA.
2001-02-07)
Admiral Perry is hiking to a lonely outpost in Alaska that is 6 days
from the closest town of Shungnak.
One hiker can carry only enough food and water for four days.
As you can tell, Admiral Perry can't go alone because
his supplies wouldn't last until he reached the outpost.
What is the smallest number of people it would take to ensure that Admiral Perry
makes it to the outpost and his assistants make it back to Shungnak?
-
Let the Admiral leave with 2 assistants.
Once they have walked for 1 day, one assistant may return with 1 day's worth of food
and leave the Admiral and his other assistant with enough for 4 days each.
The next day, the second assistant may return safely with 2 day's worth of
supplies leaving one day's worth to Perry who now has enough for the 4 remaining days.
Note: If food can be dropped along the way (hidden from wild beasts),
then the Admiral can do it alone without any assistants:
The Admiral starts carrying 4 units (4u=4 days' worth of supplies) walks 1d,
leaves 2u in a stash and returns to Shungnak.
He does the same thing again so there are now 4u in the stash.
He may now start his final journey with 4u: he walks 1d (using 1u)
and picks up 1u at the stash (3u remain),
so he may carry 4u, walk another day and leaves 2u in a second stash,
before returning to the first stash where he picks up the remaining 3u.
He walks one day to arrive with 2u to the second stash.
He picks up the 2u that were stored there to walk away with 4u,
which is enough to complete the trip (since the second stash is 4d away from the goal).
The problem is that the Admiral would thus complete the trip in 12 days instead of 6
with the first solution. He's unlikely to go for this; he's an Admiral after all...
(2001-02-17)
You leave home, walk one kilometer south, then one kilometer due east
and finally one kilometer north. If you're home again at the end of your
walk, where's home?
-
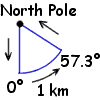
This is a great classic whose complete solution is more intricate
than it seems at first glance.
The intended solution of the puzzle was probably
"at the North Pole" (see figure to the right).
This first solution is so obvious and overwhelming that it is tempting to stop
at that and overlook a whole set of totally different solutions near the South Pole:
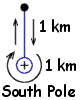
The second leg of your journey ("due east") could be a circular path one kilometer
in circumference around the South Pole (its radius is about 159.155 m).
Therefore, "home" could be anywhere at a distance of about 1159.155 m
from the South Pole: The first leg of your journey (due south) will lead you to this
circular path at some point A. Walking due east for 1000 m will take you
all the way around the circle back to point A from which you will get home
by walking a kilometer due north...
Now, it's also possible to have a circle 500 m in circumference as the second
leg of the trip. By walking 1000 m on it, you just travel twice around the
circle but end up back to A just the same.
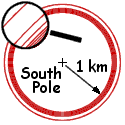This means that "home" could also be
about 1079.577 from the South pole.
Obviously now, for any positive integer n, any circular path 1/n km in length
would be an acceptable second leg of your walk.
All told, there is an infinite family of circles around the
South Pole were your "home" could be.
Final answer: Your home is either at the
North Pole or at a distance from the South Pole roughly equal to
(1 + 1/2pn) km
, for some positive integer n.
NOTE:
I had to say "roughly equal to" because the circumference of a small
"circle" drawn on a curved surface is not quite equal to 2p
times the "radius" which can be measured on that surface:
On a sphere of radius R, the distance d measured on the surface is along an arc
of a great circle (that's indeed the shortest possible distance). If the "radius"
d of a circle is measured in that way, its circumference is only
2p[R sin(d/R)]
(since the bracketed quantity is the actual radius of that circle in 3D space).
For small values of x=d/R, we have
sin(x) »
x (1-x 2/6),
and
1/sin(x) »
1/x (1+x 2/6).
Before we apply this to the above situation, we may stop to consider what is
theoretically the best value to use for R around the South Pole
(this may seem like a ludicrous concern --and it is--
but we are already into ludicrous precision
at this point, so we may as well learn something from this):
First, consider the Reference Ellipsoid (the defined regular shape with respect
to which professionals are charting the irregularities of the Earth's so-called "sea-level",
which is an equipotential surface averaged over time at each point of the Globe).
Its "equatorial radius" is defined as precisely equal to
a=6378137 m, whereas the "polar radius" (i.e. half the distance between
the North Pole and the South Pole) is about 6356752.3141404 m. This makes the
radius of curvature of the Meridian at the South Pole equal to
a 2/b or 6399593.6258639 m, for this
surface of reference. Now, the South Pole is not at sea level, but on an elevated
plateau at about 2835 m of altitude (with an unbelievably thick layer of about 8800'
feet of ice, which accounts for almost 95% of that altitude). This altitude is to be
essentially added to the radius of curvature of the "sea-level" reference meridian.
Therefore, if the surface at the South Pole was perfectly level and
smooth, it would be extremely close to the surface of a sphere with a radius R of about
6402428 m. This would make the tiny quantity
1/(6 R 2 )
(used in the "final" result below) equal to about
4.066 10-9
All told, we may now state with more (ludicrous) precision that "home" could be either on
the North Pole or at a distance from the South Pole very close to:
[ 1 + 1/2pn
(1 + (4.066 10-9)/n 2 ) ] km
, for some positive integer n.
One last word about points at a distance of exactly 1 km from the North Pole:
If your "home" is there, walking a kilometer south will bring you to the South Pole
itself. From there, you can only walk north and could therefore not perform the
second leg of the trip ("due east") at all. Such points are therefore not
solutions of the problem as stated (but there are infinitely many solutions
in any neighborhood of them which are solutions.
Of course no point whose distance
to the South Pole is less than 1 km;
can be a solution either, since such a starting point does not
even allow you to complete the first leg (i.e. walk 1 km due south)...
ZWEAV
(2001-03-02)
[Bogglers
(Oct. 2000
Discover)
by Scott Kim]
The city of Icosapolis has four rows of five houses each [in a rectangular grid].
You have a contract to paint all 20 houses.
It takes your crew one day to paint a house,
and then it takes three days for the paint to dry on that house.
Local laws forbid you to paint next to a house with wet paint,
either horizontally, vertically, or diagonally.
Determine an order in which you can paint all 20 houses in just 20 days.
| 13 |
9 |
19 |
7 |
11 |
| 5 | 1 | 14 | 3 | 17 |
| 16 | 10 | 20 | 8 | 12 |
| 6 | 2 | 15 | 4 | 18 |
You want to number each of the 20 grid locations from 1 to 20 in such a way that the
difference between two adjacent numbers is never less than 4.
Here's one solution:
Joyce E. Minowitz
(2002-11-06; e-mail)
Back in the year 1936, people born in 1892 were able to make
an unusual mathematical boast,
a boast that people born in 1980 will be able to make
at some time during the 21st century.
John Stuart Mill, the English philosopher and economist,
would also have been able to make the same boast, had he noticed it.
Given that he was born in the 19th century, can you tell me which year?
John Stuart Mill was born in 1806.
In 1936, people born in 1892 turned 44, which is the square root of 1936.
Years that are exact squares are rare enough:
422 = 1764,
432 = 1849,
442 = 1936 and
452 = 2025.
The last of these does correspond to the same pattern for people born in
2025-45 = 1980, whereas 1849-43
gives 1806 as the only possible answer for a birthdate in the 19th century.
The "unusual boast" which John Stuart Mill could have made when he turned 43
(in 1849) was to have an age whose square was the current year.
thedhsgulie
(2001-03-21)
[This is for extra credit; I got my teacher's permission to post these
problems of the day on the Internet.]
- 3 chickens and 1 duck sold for as much as 2 geese.
1 chicken 2 ducks and 3 geese sold for $25.
If each sold for a whole number of dollars, what was the price of each?
- Wigglesworth has a gold chain of seven links.
An artist friend offers to sketch each of the seven members of Wigglesworth's family
for one gold link per portrait, but wants to be paid for each portrait at its completion.
What's the least number of links that have to be cut?
- When a shepherd counts his sheep by 2's 3's 4's 5's or 6's there is 1 left over.
When he counts them by 7 there are none left over.
What's the smallest number he can have?
- A cube of wood 3 inch on each edge is to be cut into 1-inch cubes.
After each cut, the pieces may be stacked in any way desired before making the next cut.
What is the smallest number of cuts required?
- Veritas always speaks the truth, and Prevars always lie.
A stranger in their country meets a party of 3 and asks to which race each belongs.
The first one mumbles an answer, which the stranger cannot understand.
The second says: "He said he was a Prevars." The third says to the second: "You're a liar!"
Of what race was the third?
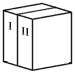
- Volumes I and II of an encyclopedia set stand side by side on a bookshelf.
A bookworm begins at page one of volume I and burrows straight
through to the last page of volume II. Each cover is 1/8 inch thick,
and each book (without the covers) is 2 inches thick.
How far does the bookworm burrow?
-
I'll just give you the answers so you can check your own solutions
(with a big HINT each time,
so you cannot possibly get stuck
):
- A chicken is $2, a duck is $4, a goose is $5.
(HINT:3x+y=2z, x+2y=25-3z implies 5x=7z-25 and 5y=75-11z,
so z must be a multiple of 5, say z=5n, x=7n-5, y=15-11n. What integer must n be?)
- Just one! (HINT:
Cutting link #3 leaves 3 pieces, with 1,2 and 4 links.)
- 301. (HINT:
The smallest multiple of 7 of the form 60n+1.)
This is an old question: It appears in
Fibonacci's Liber Abaci (1202).
- Six. (HINT: Each face of the central cube
must appear in a separate cut.)
- Veritas.
(HINT: What the second says cannot possibly be right.)
- The bookworm's burrow is only 1/4".
(HINT: Volume I is to the left of II.)
 (2004-03-27)
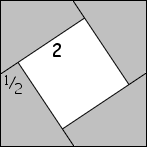
Make a square of side Ö13
with the least number of pieces cut from two squares of sides 2 and 3.
You may want to turn this dissection into a
proof
of the Pythagorean theorem, named after
Henry Perigal (1801-1898)
who rediscovered it in 1830.
Harry J.
Smith (2001-12-19)
A chauffeur always arrives at the train station at five o'clock sharp to pick up his boss
and drive him home.
One day, the boss arrives an hour early, starts walking home,
and is eventually picked up.
He is home 20 minutes earlier than usual.
How long did the boss walk before he was picked up by the chauffeur?
[from the book "Solve It" by James F. Fix]
HINT: Look at it from the chauffeur's perspective.
(Click here for solution.)
Leonard
Fibonacci,
800 years ago! (2002-02-01)
There were two men.
The first had 3 small loaves of bread and the other 2.
They walked to a spring, where they sat down and started eating.
A soldier joined them and shared their meal.
Each of the 3 men ate the same amount.
When the soldier departed, he left 5 bezants to pay for his meal.
The first man took 3 bezants, since he had 3 loaves, whereas the other took
the remaining 2 bezants for his 2 loaves.
Was the division fair? [from Liber Abaci, published in AD 1202]
-
No.
Each man ate a third of the five loaves (5/3).
Therefore, the first man gave 4/3
to the soldier (and kept 5/3 for himself),
whereas the second man gave only 1/3 (and ate 5/3).
The soldier's money should have been divided in proportion of the amount of food each
man gave to the soldier.
As these quantities are in a 4 to 1 ratio,
the first man should have taken 4 coins and the second man only 1 coin.
The real problem with this puzzle has to do with the value of a bezant...
The bezant was a gold coin,
and five of these would have been an outlandish price to pay for a meal...
Was this poorly translated or was Fibonacci really out of touch with
money and/or economic reality?
The "bezant" was also called "solidus byzantius" (or just "byzantius").
It was the gold coin introduced (under the name of solidus aureus)
around AD 315 by Roman emperor Constantine the Great,
a few years before he moved the capital of the Empire to Byzantium (Constantinople)
in AD 330.
This famous coin kept circulating under various guises for more than a millenium.
The name "bezant" is still commonly used in heraldry for
a golden disk.
The alternate name solidus is itself the root of
the names of various other coins,
including the British shilling and the French sou (formerly sol),
both of which eventually stood for a much smaller amount of money than
a bezant did during the times of Fibonacci.
Reference: Leonard of Pisa
by Joseph and Fances Gies © 1969,
reprinted by New Classics Library, Gainesville GA,
ISBN 0-317578-49-9.
The above "portrait" of Fibonacci is clipped from the cover of that book,
as designed by Enrico Amo.
Actually, we do not know what Fibonacci looked like.
(2002-11-16) The Fork in the Road
There's a fork in the road to Heaven, where one way leads to Hell.
At this fork in the road, two twin brothers live who are exactly alike,
except that one always tells the truth and the other one always lies.
What single question can you ask one of them to find the way to Heaven?
This simple riddle is probably an ancient one (in one form or another),
but we don't know anything about its history.
Please, let
us know if you do.
Answer: Point to one of the two ways and ask one brother
this
simple question.
If he answers "Yes" it's the way to Heaven, if he says "No", run the other way.
|
