Timelike-coordinates of quadrivectors appear first (not last).
Vectorial quantities are boldfaced;
lowercase symbols are used for 3D vectors, capitalization for 4-vectors:
(2003-11-03)
Observers in Motion: The Lorentz Transform
How are the coordinates in two uniformly moving systems related?
In the framework of the Special Theory of Relativity, such coordinates are
linearly related. Nonlinear relations are the subject of General Relativity,
where linear transforms
only apply to infinitesimal coordinates (cdt,dx,dy,dz).
Call t,x,y,z the coordinates in one system (S) and
t',x',y',z' the coordinates in the other (S').
Assume the axes are so oriented that motion is along the x-axis of S which is also the
x'-axis of S'. For points on that invariant axis, y,z,y',z' are zero,
and we have to find proper dimensionless coefficients aij in the relations:
ct' = a00 ct + a01 x
x' = a10 ct + a11 x
In this, c is the speed of light in a vacuum (now best called
Einstein's constant) which the basic tenet of Relativity
requires to be the same for all observers.
That is, (x±ct) is zero if and only if
(x'±ct') is. Now, we have the linear relations:
x'+ct' =
(a10+ a00 ) ct
+
(a11+ a01 ) x
x'-ct' =
(a10- a00 ) ct
+
(a11- a01 ) x
The aforementioned condition(s) can only be met if the coefficients of x and ct
on the right hand side of each equation are respectively proportional to
the coefficients of x' and ct' on the left hand side. Namely:
a10+ a00
=
a11+ a01
a10- a00
=
a01- a11
Adding or subtracting these two equations yields:
a00 = a11 and
a01 = a10 .
Introducing g = a00
and letting b be equal to -a10 / a00,
we thus obtain...
The Lorentz Transform:
ct' = g
( ct - bx )
x' = g
(-bct + x )
|
The origin of S' (x' = 0) moves at a speed v in S (x = vt).
Therefore:
Now, we have to assume that the inverse transform from S' to S is the same as the
direct transform from S to S', with only a trivial change of sign (or else,
there would be a directional preference in the Universe, which we find repugnant):
ct = g
( ct' + bx' )
x = g
( bct' + x' )
Using the prior values of ct' and x', we obtain ct = g2 (1-b2 ) ct.
So:
(2005-02-13)
Combining Collinear Velocities
How do relativistic speeds add up?
Considering the case of motions along the x-axis only,
the problem is to find the velocity w with respect to S of something moving
at velocity u in a system S' moving itself at velocity v
with respect to S.
Well, if x' = ut', the above Lorentz transform
(with b = v/c) tells us that:
x - vt =
u ( t - xv/c2 )
Solving for x, we obtain x = wt, where w is given by the following expression:
w =
|
u + v |
 |
| 1 + uv / c2 |
|
Note that, if u and v are both subluminal
(between -c and c) then so is w...
However, we need only assume that
one of the speeds is subluminal
As phrased above, v is so restricted (it's the speed of one coordinate system
in the other) whereas u could well
be a superluminal phase celerity, for example.
In that case, the result w is superluminal as well.
Nothing is subluminal for one observer and superluminal for another,
provided all observers have subluminal motion with respect to each other.
(2005-05-05)
Propagation of Light in Moving Bodies (Fresnel, 1818)
Dependence of the Fresnel drag f
on the refractive index n (Fizeau).
In 1851,
Hippolyte Fizeau (1819-1896) used interferometry to determine
experimentally how the speed of a moving liquid affects the propagation of
light in it.
He found an empirical relation between the magnitude of the effect
and the refractive index (n) of the liquid... Read on.
In a transparent fluid at rest,
the [phase] celerity of light u = c / n is isotropic and
inversely proportional to the fluid's index of refraction (n).
Consider the case where the propagation of light is parallel
to the motion of the fluid.
Let v be the speed of the fluid
and w the observed celerity of light.
According to the above rule, we have:
| w |
= |
(u + v) / (1 + uv/c2 ) |
| = |
(c/n + v) / (1 + v/nc) |
| = |
c/n + v ( 1-1/n2 )
[ 1 + v/nc ] -1 |
| » |
c/n + v ( 1-1/n2 ) |
| » |
c/n + v f |
The parameter f =
1-1/n2
is known as the Fresnel drag coefficient.
It has been named after Augustin Fresnel (1788-1827)
who introduced the now obsolete
aether
drag hypothesis in 1818, to explain experiments performed by Arago in 1810.
The coefficient f would be
0 if the motion of the liquid had no influence on the propagation of light.
It would be 1 if light was entirely "carried" by the liquid,
like sound is.
What's observed looks like partial dragging.
Hippolyte Fizeau established empirically the above expression of
f in terms of the index n, by experimenting with different liquids.
Although Fizeau's relation can be derived without resorting to the principle
of relativity (Lorentz did it)
Einstein considered it an excellent experimental test of
Special Relativity.
(2005-07-27)
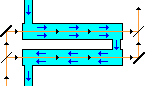
Harress-Sagnac Effect (using mirrors or fiber optics)
Rotation rate of an optical loop is revealed by interfering opposite beams.
The Sagnac effect
is a mainly nonrelativistic effect observed
when two coherent light beams (which may come from a single source through
a half-silvered mirror)
travel in opposite directions around an optical loop.
When the apparatus rotates, a phase difference is observed which is essentially
proportional to both the pulsatance w
[the rotation rate in rad/s]
and the area of the loop (actually,
the apparent area, for a distant observer located
on the axis of rotation).
The thing is not to be interpreted
as some obscure change in the celerity of light, supposedly due to rotation
(dwelling on this fallacious point is a misguided endeavor).
It's simply that the beams must travel different distances
to their rendezvous, at a point which will have moved
toward one beam and away from the other, by the time they get there !
The loop may be a polygonal path, with a mirror at each corner
(light travels at speed c between mirrors).
Alternately, fiber optics may be used so light travels at a celerity c/n
relative to the loop
[ n being the refractive index of the optical material ]
via ordinary total internal reflection (TIR).
In some of the so-called "laser gyroscopes" (devised around 1963)
of modern guidance systems, the latter method is now used
to produce a resonant frequency proportional to the rate of rotation.
One advantage over mirrors is that a fiber optic cable can easily be coiled to
increase the effective area of the loop
within a compact volume.
Rotation rates around 5 ´ 10 -11 rad / s
have actually been detected this way...
We consider only the case of a circular loop, of radius R,
rotating about its axis
(note that n = 1 approximates a regular
polygonal path with many mirrors).
Let's measure positively counterclockwise angles (that's the usual convention)
and assume that the loop is rotating in this positive direction.
Euclidean geometry remains valid for a fixed observer, who thus sees each point
of the loop travel a distance 2pR
in a time 2p/w.
Therefore, the nonrelativistic expression for the speed v
of each point of the loop does hold:
v = wR.
(The Fitzgerald-Lorentz contraction applies to the length of moving objects, not
to the space they travel.)
Using this value of v in the (exact) expression from the
previous article, we obtain the
value for the celerity w of either beam in the moving loop,
from our fixed viewpoint
("±" means
"+" for the positive beam and "-" for the other).
w ±
=
± c/n
+ wR
( 1-1/n2 )
[ 1 ± wR/nc ] -1
This signed quantity is, of course, equal to
± c
when n = 1.
Now, if both beams start from the same point at t = 0,
this point will be at an angle wt
when the beam reaches it again after one turn, so that t is a solution
of the equation:
t w ±
/ R = wt
± 2p
Solving for t, we get:
t- = 2pR /
( -w- + wR )
t+ = 2pR /
( w+ - wR )
The exact values of
w ±
make n vanish from the time lag ! [2005-07-27]
Sagnac Time Lag
(inertial observer at rest at the center of rotation)
| t+ -
t-
=
Dt
= |
4p R 2
w |
 |
|
c 2 - w 2 R 2 |
| |
With ordinary objects, the above is undistinguishable from
4p R 2
w / c2
and is thus proportional to the rotation
w.
Indeed, the speed wR of the circumference is
much lower than the speed of light
(the relative error is about
1.22 ´10-13
for a 10 cm radius at 10 000 rpm).
Even for relativistic things, the above denominator must be positive
(there's no such thing as a large rotating "solid").
History of the Harress-Sagnac Effect :
The Sagnac effect was actually first dreamt of by
Albert A. Michelson in 1904.
In 1911, Francis Harress tried to substitute glass for the
liquids used in Fizeau's investigations.
He had the idea to observe rotating rings of glass, but could clearly do so
only at fixed points of such rings...
As we've discovered theoretically in the above discussion, the resulting effect
does not depend on the index of refraction involved !
Although Harress failed to understand his experimental results,
the effect is still known as Harress-Sagnac,
mostly in the context of fiber optics.
Iin 1913, the French physicist Georges Sagnac (1869-1926) published his own
experimental results and properly described the effect now named after him.
The prior observation by Harress of the effect's "fiber optics version"
was noted later.
Michelson and Gale used this effect in 1925 to measure the absolute rotation
of the Earth, with a rectangular optical loop
0.2 mile wide and 0.4 mile long.
Sagnac Effect
|
Ring
Laser Project
|
Wikipedia
gerry (2002-06-27)
Relativistic Limit of a Relative Speed
What is w = (u-v) / (1-uv/c2 ) as both u and v approach c ?
Answer: The quantity w doesn't have a definite limit as both u and v approach c.
This formula for w describes how [collinear] relativistic velocities are combined:
Consider a straight railroad track where a train (U) moves at speed u
and another train (V) moves at speed v
(both speeds being measured relative to some platform
on which the "observer" is located).
According to the Special Theory of Relativity
(see above) the quantity
w = (u-v) /
(1-uv/c2 )
is simply what the speed of train U would be for an observer located on train V.
If the observation platform is on a fast rocket moving
parallel to the railroad tracks and approaching the speed of light c
(with respect to the tracks),
both u and v will be close to c.
Yet, the quantity w remains a low number (like 10 mph or 20 mph)
equal to the speed of one train relative to the other.
This relative speed is not affected by how fast an irrelevant nearby rocket
might be moving...
To make this relativistic math more transparent, you may want to consider
rapidity
instead of speed:
If u is the speed, the corresponding rapidity x is defined as
x =
tanh-1 (u/c).
The interesting thing is that rapidities are additive,
whereas speeds are not:
The rapidities x, y, z corresponding to the above speeds u, v, w are thus related by
the much simpler equation:
z = x - y
As speeds approach c,
rapidities approach infinity and the question becomes:
What's the limit of z = x-y
when both x and y become infinite?
Answer: Such a limit is clearly undefined.
Take your pick, use either the physical or the mathematical approach...
gerry (2002-06-30) [follow-up to the previous article]
What's the relative velocity of two photons?
The velocity of object B relative to object A is the velocity of B measured in the frame of
reference where A has zero speed.
When A is a photon,
we are in trouble with this definition,
because there is no such proper frame of reference.
The question is thus to determine if/when the above definition
can be consistently extended to include objects moving at speed c.
Such an extension exists, except in the very special case of two photons moving
in exactly the same direction, where the notion of "relative speed"
breaks down completely
(as shown in the above discussion of the relativistic
formula for the "addition" of parallel velocities).
If A is a photon but B is not also moving at speed c,
we may still reach a firm conclusion by noticing
that the velocity of B relative to A must be the opposite of the velocity of
A relative to B (which is well-defined, unless B moves at speed c).
Let's consider now the case of two photons of velocities u and v.
These two velocities are 3D vectors of length c; the corresponding 4-vectors
(c,u) and (c,v) have zero 4-dimensional "length".
If u and v are not equal (that's to say that the two photons
have different directions) the 3D length
||u-v|| is nonzero
and it turns out that the relative velocity of two objects chasing the
two photons (at sub-c speed) approaches a definite limit when the velocities
of the chasers both approach the velocities of their respective chasees.
This limit is:
c (u-v) / ||u-v||
If we have to define the relative velocity of two photons moving along different
directions (possibly opposite, but not equal),
this is the only sensible way to do it.
On the other hand, if u and v are equal, we are back to our
previous discussion:
Two sub-c chasers with any arbitrary relative velocity
(not necessarily collinear with u = v)
could both approach the velocity (u = v) of both photons.
Therefore, there is no continuous way to define the relative velocities of two photons
moving in the same direction.
Having said this, we may or may not find it useful to state
(rather arbitrarily) that two such photons have zero relative speed.
However, we failed to find a compelling reason for this "obvious" choice
and cannot guarantee that it would not lead to a paradox of some kind...
(2005-04-14)
Minkowski Space and 4-Vectors
A scalar and a 3-vector obeying the Lorentz rule form a 4-vector...

A scalar quantity a whose value does not depend on the
coordinate system used to locate
space-time events is called a relativistic invariant.
The 4-dimensional gradient of such a scalar is the following 4-vector:
Grad a =
(-1/c ¶a/¶t ,
grad a ) =
(-1/c ¶a/¶t ,
¶a/¶x ,
¶a/¶y ,
¶a/¶z )
Applying this definition in another coordinate system leads to coordinates
that are indeed obtained from the above ones via the relevant Lorentz transform.
(2005-04-16)
Wave and Phase: Wave Vector = Phase Gradient
An Introduction to Four-Dimensional Wave Vectors.
The phase j
of a periodic phenomenum describes
its position in the cycle: a crest, descending, a trough, ascending, etc.
This does not depend on whatever coordinate system we may use to locate the event:
j is a relativistic invariant.
The phase j of an
ideal planar wave at a given point
R = (ct,r) is given by the following relation,
up to some irrelevant additive constant:
j = wt
- k.r
The pulsatance (w) is proportional to the wave's
frequency (n),
whereas the magnitude of the 3D wave-vector (k) is tied to
the wavelength (l), namely:
The celerity of the wave (its phase speed) is the product
u = ln.
K = (w/c, k) is a
4-vector because it's the
4D gradient of a scalar invariant:
K =
(w/c , k) =
Grad(-j)
This quadrivector is known as the four-dimensional wave vector.
(2005-05-03)
Doppler Shift.
Relativistic Transverse Doppler Effect
The radial effect is multiplied by an isotropic relativistic factor.
Among redshift factors, the classical
Doppler effect comes from a changing distance between the
observer and the source of radiation.
Another type of redshift is also due to local relative motion.
It's entirely relativistic and applies even in the case of
transverse motion, where this distance does not change:
If the source is moving at velocity v, its proper pulsatance
w0 = 2pn0
(in the frame where it's at rest) is given by the
Lorentz transform for the wave-vector:
w0 /c
= g
( w/c - b k x )
= g
( w/c - k.v/c )
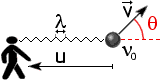
Therefore, calling q the angle between v and
the direction of observation (-k) we have:
n0
= g
( n + cos(q)
||v|| / l )
Introducing the celerity
of the signal u = ln
(not necessarily c) we obtain:
|  | |
| |
l n0 |
Ö |
1 -
v2/c2 |
=
u + v cos q
| |
|
This is merely the classical (radial) Doppler effect,
with an extra relativistic factor
which comes from the observed stretching of time in a moving source.
The above is of the form
l n0' = u' :
The classical radial celerity (u') is
the observed wavelength (l)
multiplied by a relativistically adjusted frequency
(n0').
A Dubious Academic Tradition:
Things are more obscure when the above expression is "simplified" for light in
a vacuum (u = c)
in 3 special cases which are popular with textbook writers:
Relativistic
Doppler effect for light (u = c): Values of
1 + z = l / l 0| Outbound (q = 0) |
Transverse (q = ±p/2) |
Inbound (q = p) |
|---|
| [ (1+v/c) / (1-v/c) ] ½ |
1 / (1-v2/c2 ) ½ |
[ (1-v/c) / (1+v/c) ] ½ |
(2005-04-14)
Energy (E) and Momentum (P)
E/c and P form a 4-vector (i.e., they transform like ct and r).

Louis Vlemincq
(Belgium; e-mail 2005-04-14)
Kinetic Energy
What's the relation between E = m c 2
and the formula E = ½ m v 2 ?
The relativistic energy of a particle of rest mass m and speed v is:
| E =
(m g) c 2 = |
m c 2 |
 |
|  |
|  |
| Ö |
1 - v2/c2 |
|
The symbol m is often used for the actual mass
(m g).
We don't do this here.
Under the assumption that v is much smaller that c, a good approximation for E
is obtained from the Taylor expansion of the above:
E = mc 2 ( 1
+ 1/2 (v/c)2
+ 3/8 (v/c)4
+ 5/16 (v/c)6
+ ...
At low speed, we may just keep the first two terms of this series:
E »
mc 2 +
½ mv 2
In prerelativistic mechanics, the first term is irrelevant because it's a constant, whereas
the second term is called kinetic energy.
Actually, the first term was originally conjectured by Einstein because of the above
considerations: It's just mathematically simpler to assume that
a motionless body of mass m already has an energy
mc2.
This explains painlessly the so-called mass defect observed
in the decay of radioactive elements :
A nuclear decay always leaves remnants whose rest masses add up to less than the mass
of the original nucleus. The balance of the energy appears in the form
of either kinetic energy or radiation...
The relation E = m c 2 has
been verified directly
with countless experiments in nuclear physics, starting with
Cockcroft
and Walton's accelerator, in 1932.
In 1938, Otto Hahn and Fritz Strassmann observed that Barium
is produced when Uranium is bombarded with neutrons.
In 1939,
Lise
Meitner and Otto Frisch interpreted this result as an induced
fission of the Uranium atom.
(2005-04-14)
Photons and Other Massless Particles
To have a finite energy, a massless particle must travel at speed c.
Particles travelling at speed c can only have a finite energy if they have
zero rest mass ; they only exist in motion
(always at speed c).
In this case, we must use a quantum expression of the energy, in terms of an associated
wave: The energy of a photon of frequency n
is hn,
where h is Planck's constant.
This relation was proposed by Einstein (1905) in his explanation of the laws of
the photoelectric effect (for which he received
the Nobel Prize in 1921)
which may be construed as a formal discovery of the photon...



At first, Isaac Newton (1643-1727)
had argued that light was corpuscular
[i.e., consisting of discrete particles]
against Christiaan Huygens (1629-1695)
who held the view that it was undulatory [wavelike].
The viewpoint of the latter was revived in 1803, when Thomas Young's
double-slit experiment
proved light was capable of interference.
The same doctrine was reinforced when James Clerk Maxwell (1831-1879)
put forth his famous differential equations
governing electromagnetism in general,
and light in particular [at a macroscopic level].
Max Planck (1858-1947) also believed strictly in the wave nature of light,
even after his own success in explaining the blackbody spectrum
by assuming matter and radiation could only exchange energy in
packets ("quanta") proportional to the radiation's frequency.
Thus, it was a revolutionary proposal of Einstein's that Planck's packets of energy could
actually be related to the particles of radiation envisioned by Newton.
A generalization to electrons and other subluminal particles
was proposed by the French physicist Louis de Broglie,
who put forth a new principle establishing
the dual corpuscular and undulatory nature
of everything, as discussed next.
 (2005-04-16)
The Principle of de Broglie is Relativistic
(2005-04-16)
The Principle of de Broglie is Relativistic
Corpuscular and undulatory duality, as proposed in 1923/1924.
In 1923, the French physicist
Louis
de Broglie (1892-1987;
Nobel 1929) was still a graduate
student at the Sorbonne when he proposed the idea of matter waves,
which he defended successfully in 1924 (with the support of Einstein himself)
in front of a doctoral committee which included
Paul Langevin (1872-1946).
At the time,
de Broglie stated that his proposed matter waves might
be observable in experiments involving crystal diffraction with electrons.
Such experimental confirmations came in 1927, with two independent experiments:
one by Clinton J. Davisson (1881-1958;
Nobel 1937)
and Lester H. Germer (1896-1971), the other by G.P. Thomson (1892-1975;
Nobel 1937)...
Ironically, George Paget Thomson thus demonstrated the undulatory nature of
electrons, whose corpuscular properties were established three decades earlier
by his own father, J.J. Thomson
(1856-1940; Nobel 1906).
De Broglie's idea was that any particle is associated with a so-called pilot wave:
The momentum of one and the wave-vector of the other are proportional and
the coefficient of proportionality is a universal constant.
We'll state de Broglie's principle
using the 4-dimensional wave-vector introduced
above:
| K | = |
(w/c , k) =
Grad(-j)
|
| w | = |
2p n |
| || k || | = |
2p / l |
De Broglie's Principle Expressed Relativistically :
Louis de Broglie proposed that any particle of
4D momentum P = (E/c, p)
was "associated with" a wave of
(4D) wave-vector K proportional to P, namely:
P =
 K =
(h/2p) K
[ h is Planck's constant ]
K =
(h/2p) K
[ h is Planck's constant ]
This 4D equality breaks down into a scalar component and a (3D) vectorial component.
The former is Planck's relation, the latter is de Broglie's relation,
usually stated using only the magnitude
p = || p || of the 3D-momentum:
The Relation between Celerity (u)
and Group Speed (v) :
The above relations make the celerity u = ln
equal to E/p.
For a particle of rest mass m and speed v, we have:
(mc)2 =
(E/c)2 - p 2. Therefore:
1 / u 2
=
(p/E)2
=
1 / c 2 - (mc/E)2
=
(1-(1-(v/c)2 )) / c 2
=
(v/c 2 ) 2
This establishes an extremely simple relation:
The [phase] celerity (u) for a massive particle is thus greater than c,
as energy and information travel at the group speed (v),
which remains lower than c.
 (2005-04-14)
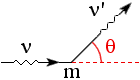
The Compton Effect
(2005-04-14)
The Compton Effect
The frequency of a photon changes when it collides with an electron
(of rest mass m).
Compton scattering is a deflection of X-rays by matter which is observed
to occur with a shift in the frequency
(n) that depends on the angle of
deflection (q).
This was explained by Arthur H. Compton
(1892-1962; Nobel 1927)
in terms of individual collisions between incoming photons and recoiling electrons:
In a system where the target electron (of rest mass m) is at rest,
its 4-momentum is (mc,0).
The incoming photon moves along the x-axis and goes out
in the (x,y) plane, at an angle q
from Ox. Now, energy-momentum is conserved:
After the shock, the 4-momentum P
of the electron is thus obtained by subtracting the momentum of the outgoing photon
from the sum of the two initial 4-momenta.
The Minkowski square of the electron's 4-momentum
is -(mc)2, therefore:
- m 2 c 4 =
-(mc2 + hn
-
hn' ) 2 +
( hn - hn'
cos q ) 2 +
( hn' sin q ) 2
Using the
Compton frequency of the electron
( nc = m c2 / h )
this gives:
|
n'
=
n
/
[ 1 + (1 - cos q )
n / nc ]
|
The
Compton wavelength of the
electron ( lc = h / mc )
is more often used:
|
l'
=
l [ 1 +
(1 - cos q )
lc / l ]
|
With energetic photons (gamma rays)
the target electrons may recoil at high speed and subsequently
cause bluish cherenkov radiation in transparent bodies.
(2003-11-15)
Relativistic Elastic Collisions
A simple relation between transfer of energy and change in momentum.
dE = v.dp
(v is the velocity of the center of mass). Here are the details:
If two particles (1 and 2) collide but retain their respective identities,
we may define the energy and the momentum lost by one and gained by the other:
| dE |
| = |
E'1 - E1 |
= |
- ( E'2 -
E2 ) |
= |
y c |
| dp |
| = |
p'1 - p1 |
= |
- ( p'2 -
p2 ) |
= |
x u [ with ||u|| = 1 ] |
The scalars x and y are introduced for convenience, so is the unit vector u,
which is uniquely defined, unless no shock takes place
(dp = 0).
We also introduce:
pi
=
u . pi
=
(Ei / c 2 ) vi
A collision is said to be elastic
when each rest mass is conserved, namely:
| E'12 / c2 -
p'12 |
= |
E12 / c2 -
p12
|
| E'22 / c2 -
p'22 |
= |
E22 / c2 -
p22
|
In the form
(p'i - pi
).(p'i + pi )
=
(E'i - Ei )
(E'i + Ei ) / c 2
these two read:
| x ( 2 p1 + x ) |
= |
y ( 2 E1 / c + y ) |
| x ( 2 p2 - x ) |
= |
y ( 2 E2 / c - y ) |
Adding both equations, we obtain
x ( p1 + p2 ) =
y ( E1 + E2 ) / c
Using this relation, we may multiply either of the previous equations by
( E1 + E2 ) / cx
(as x is nonzero) and obtain the second equation of the following
linear system:
| x ( p1 + p2 ) |
- |
y ( E1 + E2 ) / c |
= |
0 |
| x ( E1 + E2 ) / c |
- |
y ( p1 + p2 ) |
= |
2 ( E1 p2 -
E2 p1 ) |
By itself, the first equation says that
dE = v.dp
(as advertised) where the
vector v is the velocity of the center of mass, namely:
v =
( p1 + p2 ) c 2 /
( E1 + E2 )

(2005-05-05)
[ Blue ] Cherenkov Radiation
The Cherenkov effect occurs when a charged particle
moves faster than the celerity of light.
In a dispersive medium like a liquid or a gas, the celerity of light depends
on frequency. Normally, the celerity of visible light is below
Einstein's constant (c) while the celerity of
X-rays is above it.
( It's the group speed which may never exceed c.
Phase celerity is another matter entirely.)
Radioactive sources make nearby transparent bodies emit a bluish glow which
Marie Curie first
noticed in 1910, about radium salts in distilled water.
Part of this glow may consist of ordinary luminescence from various impurities.
This is what the whole thing was mistaken for until 1926-29, when the French physicist
Lucien I. Mallet investigated the phenomenon and found it to have a
continuous spectrum, unlike ordinary fluorescence.
This was further studied between 1934 and 1937 by Pavel A. Cherenkov (1904-1990)
who established, in particular, that the radiation came primarily from fast electrons
disloged by Compton collisions with energetic gamma-rays.
The final mathematical explanation was worked out by two of his colleagues of the
Lebedev Physical Institute of Moscow,
Il'ja M. Frank and
Igor Y. Tamm, following the 1936 discovery of the particular geometry
of the Cherenkov beam.
For this, the three men became the first Russians ever to be awarded the
Nobel Prize in Physics,
in 1958.
Cherenkov radiation is entirely different from so-called bremsstrahlung,
the electromagnetic radiation emitted when a charged particle is accelerated
(e.g., as it collides with atoms).
A heavy particle causes less bremsstrahlung than
a lighter one of the same speed, but the Cherenkov emission is the same.
The Cherenkov effect is to light what the
sonic boom is to sound. Kind of :

The effect is also called "Cerenkov-Mallet", especially in French texts.
"Cerenkov" and "Cherenkov" are equally acceptable transliterations.
Cherenkov Radiation by Philip Gibbs
|
Cherenkov Radiation
by Emma Ona Wilhelmi



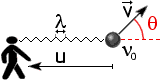
 (2005-04-14)
The Compton Effect
(2005-04-14)
The Compton Effect
