The best way to find small prime factors is simply to try them all out...
However, unless a prior sequence of small primes is available,
it's simpler to use a sequence of trial divisors (starting with 2) which includes
all primes without ruling out composite numbers.
For example, we may try 2 and all odd numbers. We may also
try 2, 3, 5 and integers not multiple of these, namely
(for k = 0,1,2,3...):
30k+7, 30k+11, 30k+13, 30k+17, 30k+19, 30k+23, 30k+29, 30k+31
In such an increasing sequence of trial divisors,
the first number (p) which is found to divide n is necessarily prime
(since any divisor of p would have been found earlier as a divisor of n).
Once such a divisor is found, the search may be resumed
for the lesser number n/p, considering only divisors at least equal to p.
The process may be aborted when the trial divisor exceeds the square root of
the number to factor, as the latter is then surely prime...
If you fail to find small factors, it's probably a good idea to
try a primality test
before going any further (preferably using some other method of factorization).
If the number n is prime [beyond a reasonable doubt] the search for its smallest prime
factor may end with n itself, well before the trial divisor
reaches Ön.
With this added primality test, trial division
finds all factors of a
composite number in a time roughly proportional to its
second-largest prime factor.
By contrast, the running time of the r
method (discussed next)
is roughly the square root of that:
In a given amount of time, the r method may find
factors with about twice as many digits as those obtained by trial division.
The following article introduces some of the ideas underlying
Pollard's r factoring...
A sequence
U0,
U1,
U2 ...
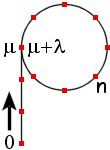
is called ultimately periodic
with preperiod m
and period l when
Un+l = Un for any
n at least equal to m,
but not for n = m-1
(if m ¹ 0).
If each term of a sequence is a function of the previous one, and if only finitely
many values are allowed, then the sequence is necessarily
ultimately periodic.
(HINT: Since only finitely many values are possible,
one will eventually be met again.
This marks the beginning of a regular cycle in a recursive sequence.)
Recursively-defined sequences with finitely many values :
Such a sequence (U) is defined by its initial value U0
and its recursion relation
Un+1 = f (Un )
over a finite set of p allowed values, like {0,1,2,3 ... p-1}.
The recursive definition of U endows it with a nice property:
{ Un = Un+q }
Û
{ n ³ m and
l | q }
This may be used [with n = q] to show that there's a unique
index n between m (included)
and m+l (excluded)
such that Un = U2n.
(Note that l divides n.)
n = 0 ; x = U0 ; y = x
repeat
n = n+1 ; x = f (x)
; y = f ( f (y))
until x = y
For the record, a useless expression for
the index n (as computed above) is:
n =
l max ( 1,
é m/ l ù )
The above computation of n requires 3n calls to the function f
(without ever storing more that 2 or 3 values of U ).
Once n is known, we observe that:
m is the smallest i such that
Un+i = Ui
l is the smallest i such that
Un+i = Un
We need not check both of these conditions beyond the point where the
first one is met (which gives directly the preperiod m):
If the second one has already been met, we're done with
the period (l) as well.
Otherwise, we have m < l and must have
l = n
(since n divides l and is below
m+l < 2l).
All told, we may obtain m & l by using
the function f only
2m additional times.
Application to Factorization Involves a
Polynomial f :
Modulo p, the value of a polynomial f
is congruent to its value modulo pq...
If p is a factor of a large integer N, we observe that
terms of like indices in the following sequences are congruent
modulo p,
provided U0 and V0 are equal:
| Un+1 | = | f
( Un ) [ mod p ] |
| Vn+1 | = | f ( Vn )
[ mod N ] |
Therefore, if we have Ui = Uj modulo p,
then Vi- Vj
is divisible by p too, and we may retrieve p,
or some multiple D of p which divides N, via:
D = gcd ( N , Vi- Vj )
[ with i ¹ j ]
To turn this into a true factorization technique, we assume no prior knowledge of p
(and/or U). Instead, we just rely on the above result D.
When D = 1, the pair of indices (i,j) is not "magic" and we keep
searching for other possible pairs, following some predetermined scheme
(the above would call for j = 2i for successive values of i,
but there are other ways).
In the rare case where D = N,
we must abort a doomed search.
Otherwise, D is a nontrivial factor of N.
If D = N, a fresh start with a new polynomial is called for.
This is also recommended if D isn't prime and needs to be factored further...
On the other hand, if
N' = N/D isn't prime
it's a good idea to search for the factors of N'
by resuming the same sequence, modulo N'.
If we look for indices (i,j) in the form i = n and j = 2n,
then the above shows n to be less than m+l,
which is itself usually on the order of
Öp.
We may thus expect factors proportional to the square of the time spent
looking for them.
Although the algorithm discussed next uses another scheme,
it's enlightening to analyze this simple one, using the very popular polynomial
f (x) = x 2 +1 :
W0 = 1 and
Wn+1 =
Wn2 +1
| n | Factorization of
W2n- Wn |
| 1 | 3 |
| 2 | 2 5 . 3 . 7 |
| 3 | 3 3 . 5 3 . 7 .
31 . 97 .
2957 |
| 4 | 2 8 . 3 . 7 .
11 . 13 3 . 19 . 31 . 37 . 79 .
113 . 163 .
9103 .
16369 . 37633 .
3898927 .
21617899 |
| 5 | 3 . 7 .
19 . 31 . 37 . 83 .
151 . 283 . 563 . 677 3 . 821 .
13249 . 19687 . 81707 .
152777 . 459007 . 5729593 .
1571825191 .
30009484129 .
45341337176538211 .
1429595747719217881879 .
2358937632593897968703206264666894551643096860994612426386412205627 |
| 6 | 2 11 . 3 3 . 5 4 .
7 2 .
11 . 17 3 . 19 . 23 . 31 . 37 . 43 . 53 . 73 . 97 .
107 . 163 . 211 . 239 . 313 .
2039 . 2957 . 8429 . 9949 .
10861 . 13339 . 38747 . 45833 3 .
459007 . 791801 .
2822069 .
15607909 . 17008487 .
250212983 . 298814209 . 327430417 . 384223559
... etc. |
| 7 | 3 . 7 .
19 . 31 . 37 . 41 3 . 43 .
131 . 157 . 313 . 317 .
1277 3 . 2789 .
41179 .
459007 .
4012193 3 .
15607909 . 34658977
... etc. |
| 8 | 2 14 . 3 . 7 .
11 . 13 4 . 19 . 23 . 29 . 31 . 37 . 43 . 53 . 79 .
107 . 113 . 157 . 163 . 173 . 197 . 239 . 313 .
1451 . 1877 . 2153 . 2887 . 3391 . 3511 . 3539 . 3919 . 5669 . 7121 3 .
8737 . 9103 . 9949 .
13759 . 16369 . 37633 . 38747 .
459007 . 621113 3 . 677791 .
1188017 . 2331751 . 3898927 . 7418347 .
14350313 . 15607909 . 21617899 . 27975743 . 45004633
... etc. |
| 9 | 3 4 . 5 5 . 7 .
19 2 . 31 . 37 . 43 . 59 . 97 .
101 . 157 . 271 . 313 . 509 3 . 743 . 983 .
1033 . 1187 . 2039 . 2957 . 3067 . 3511 . 8429 .
13441 . 27191 . 35449 . 56813 3 . 97381 .
459007 .
7248457 .
15607909 . 17008487 . 21298769 3 . 27308977 . 45004633
... etc. |
If a prime number p first appears on the nth row of the above table,
then p would be found to divide a large integer in
n steps of the above process, athough it may remain buried
within a composite divisor whose factors first appear on the same row
(consider, for example, the six largest factors given above for n = 5).
Primes below 1096967 need
at most n = 3680 (reached for p = 967129).
The last factorization tabulated (n = 9)
is that of a 46377-digit number.
For n = 20, we're dealing with a 194516604724-digit integer,
whose divisors include the sixth power of 677 and the fourth power of 1265129.
For n = 100, we're facing a
really big number, divisible by the twelfth power
of 1265129...
Fortunately, we only use this sequence modulo
the integer to be factored.
This method is intended for the factorization of a fairly large number n,
preferably once smaller factors have been removed, using preliminary methods
which are more efficient at weeding out small or
medium-sized divisors...
As far as we know, no one has yet devised a more efficient approach for large factors.
Frustrating as this may be, this is the best we have. For now.
The basic idea is to find many numbers whose squares are congruent to
relatively small integers modulo n
(or modulo kn, for some optimized multipler k, if the
continued fraction approach is used).
Hopefully, such "small" numbers can be fully factored using only a so-called
factor base...
The factor base is a predetermined set of small primes
[together with the negative unit (-1) whenever negative residues are expected].
In some versions, one larger prime is allowed in each factorization,
in the hope that it will pop up again in the same capacity when factoring another
residue (when this happens, the two factorizations can be effectively
combined into a single factorization over the factor base only).
With enough of these, we may be able to work out so a nontrivial solution of
x 2
º y 2
and obtain a factor of n as either gcd(n,x-y) or gcd(n,x+y).

Continued Fractions :
Quadratic Sieve :
Multiple Polynomial Quadratic Sieve (MPQS)
Special Number Field Sieve (SNFS)
[General] Number Field Sieve (NFS or GNFS)