Polyhedra (3D), Polychora (4D), Polytopes (nD)
 (Jerry of Nashville, TN.
2000-11-18)
(Jerry of Nashville, TN.
2000-11-18)
What [polyhedron] has six faces?
-
A polyhedron with 6 faces is called a hexahedron.
The cube
is your most obvious hexahedron, however that's certainly not the only one.
Disregarding geometrical distortions and considering only
the underlying topology, there are 7 distinct hexahedra:
| Name of Hexahedron | Edges | Nodes |
|---|
| Triangular Dipyramid | 9 | 5 |
|---|
| Pentagonal Pyramid | 10 | 6 |
|---|
| Tetragonal Antiwedge | 10 | 6 |
|---|
| Hemiobelisk | 11 | 7 |
|---|
| Hemicube | 11 | 7 |
|---|
| Cube | 12 | 8 |
|---|
| Pentagonal Wedge | 12 | 8 |
|---|
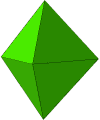
The above triangular dipyramid
has 5 vertices and 9 edges. It's the dual of a triangular prism,
and looks like two tetrahedra "glued" on a common face.
The pentagonal pyramid
has 6 vertices and 10 edges; it's a pyramid whose base is a pentagon.
Like all pyramids, the pentagonal pyramid is self-dual.
The above three hexahedra are the only ones which exist in a version where all 6 faces
are regular polygons.
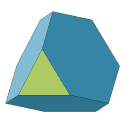
 The tetragonal antiwedge is the least symmetrical of all hexahedra;
its only possible symmetry is a 180° rotation.
This skewed hexahedron has
the same number of edges and vertices as the pentagonal pyramid.
Its faces consist of 4 triangles and 2 quadrilaterals.
Such a solid is obtained from two quadrilaterals
that share an edge [the hinge]
but do not form a triangular prism.
After adding two edges to complete the two triangles whose sides are adjacent to
the hinge, we are left with a nonplanar quadrilateral
and must choose one of its 2 diagonals as the last edge of the polyhedron.
Only one choice gives a convex polyhedron.
The tetragonal antiwedge is the least symmetrical of all hexahedra;
its only possible symmetry is a 180° rotation.
This skewed hexahedron has
the same number of edges and vertices as the pentagonal pyramid.
Its faces consist of 4 triangles and 2 quadrilaterals.
Such a solid is obtained from two quadrilaterals
that share an edge [the hinge]
but do not form a triangular prism.
After adding two edges to complete the two triangles whose sides are adjacent to
the hinge, we are left with a nonplanar quadrilateral
and must choose one of its 2 diagonals as the last edge of the polyhedron.
Only one choice gives a convex polyhedron.

Loosely speaking, there are two types of
tetragonal antiwedges which are mirror images of each other;
each is called an enantiomer, or enantiomorph of the other.
The tetragonal antiwedge is thus the simplest example of a chiral
polyhedron.
In particular, any other hexahedron can be distorted into a shape
which is its own mirror image, and the tetragonal antiwedge
may thus unambiguously be called the chiral hexahedron.
Each enantiomer is self-dual;
a tetragonal antiwedge and its dual have the same chirality.
 The other types of hexahedra are more symmetrical and simpler to visualize.
One of them may be constructed by cutting off
one of the 4 base corners of a square pyramid to create a new triangular face.
This hexahedron has 7 vertices and 11 edges.
The other types of hexahedra are more symmetrical and simpler to visualize.
One of them may be constructed by cutting off
one of the 4 base corners of a square pyramid to create a new triangular face.
This hexahedron has 7 vertices and 11 edges.
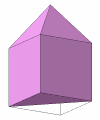 Its faces include 3 triangles, 2 quadrilaterals and 1 pentagon.
It could also be obtained by cutting an elongated square pyramid
(the technical name for an obelisk)
along a bisecting plane through the apex of the pyramid and the
diagonal of the base prism, as pictured at right.
For lack of a better term, we may therefore call this hexahedron an
hemiobelisk.
Its faces include 3 triangles, 2 quadrilaterals and 1 pentagon.
It could also be obtained by cutting an elongated square pyramid
(the technical name for an obelisk)
along a bisecting plane through the apex of the pyramid and the
diagonal of the base prism, as pictured at right.
For lack of a better term, we may therefore call this hexahedron an
hemiobelisk.
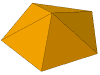
 Also with 7 vertices and 11 edges, there's a solid which we may call
a hemicube (or square hemiprism), obtained
by cutting a cube in half using a plane going through two opposite corners and
the midpoints of two edges. Its 6 faces include 2 triangles and
4 quadrilaterals.
Also with 7 vertices and 11 edges, there's a solid which we may call
a hemicube (or square hemiprism), obtained
by cutting a cube in half using a plane going through two opposite corners and
the midpoints of two edges. Its 6 faces include 2 triangles and
4 quadrilaterals.

With 8 vertices and 12 edges, the cube
(possibly distorted into some kind of irregular prism or truncated tetragonal pyramid)
is not the only solution:
Consider a tetrahedron, truncate two of its corners and you have a
pentagonal wedge.
It has as many vertices, edges and faces
as a cube, but its faces consist of 2 triangles,
2 quadrilaterals and 2 pentagons.
We can build a pentagonal wedge with 2 regular pentagons and
2 equilateral triangles, so that all edges but one are equal.
The one "exceptional" edge is the longest side in the two trapezoidal faces.
What's its length? Well, look at the
wedge "from the side" (so both pentagons project into a line) you see two similar
isosceles triangles. The base of the smaller is a regular edge seen perpendicularly
(and therefore at its real size), whereas the base of the larger triangle is the
length we're after.
The ratio of similitude is simply the ratio of the height of a regular pentagon
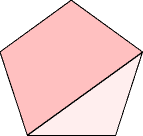 to the distance from a side to an adjacent vertex, namely
1+sin(p/5)/sin(2p/5) =
(1+Ö5)/2. A number known as the
golden ratio, which happens to be the ratio of the diagonal to the
side in a regular pentagon. The longest edge in our solid is thus
1.6180339887498948482... as long as any other.
In other words, both trapezoidal faces are congruent to the diagonal section of
a pentagonal face (pictured at right).
to the distance from a side to an adjacent vertex, namely
1+sin(p/5)/sin(2p/5) =
(1+Ö5)/2. A number known as the
golden ratio, which happens to be the ratio of the diagonal to the
side in a regular pentagon. The longest edge in our solid is thus
1.6180339887498948482... as long as any other.
In other words, both trapezoidal faces are congruent to the diagonal section of
a pentagonal face (pictured at right).
How many polyhedra have a given number of faces and/or edges?
-
 We maintain on this site an authoritative table
with the latest data.
Let's just say it's not easy to count these things.
We maintain on this site an authoritative table
with the latest data.
Let's just say it's not easy to count these things.
Polyhedra which are mirror images of each other are not counted as distinct.
In the above article, we counted 7 types of hexahedra,
but there would be 8 if we tallied separately
both chiralities of the tetragonal antiwedge.

There's only one tetrahedron:


There are two types of pentahedra:
the triangular prism and
the square pyramid.
There are 7 hexahedra (see previous article),
34 heptahedra, 257 octahedra, 2606 enneahedra, 32300 decahedra,
440564 hendecahedra, 6384634 dodecahedra, 96262938 tridecahedra, 1496225352 tetradecahedra,
etc.
BenO (Ben Ocean, 2001-07-28, via e-mail)
I'm looking for the x,y,z coordinates of the vertices in the 5 Platonic Solids,
preferably in such a way that they precisely nest within each other.
(I want to recreate and manipulate these solids in AutoCAD.)
-
The relevant data is available in topical pages from reliable sources like:
Paul Bourke,
Ron Knott,
VB Helper, etc.
| |
Regular Tetrahedron
| A | B | C | D |
|---|
| x = | 2 | 2 | -4 | 0 |
|---|
| y = | 2Ö3 |
-2Ö3 | 0 | 0 |
|---|
| z = | -Ö2 |
-Ö2 | -Ö2 |
3Ö2 |
|---|
|
Shown at right are the Cartesian coordinates of the vertices
of a regular tetrahedron ABCD centered at the origin.
These may be scaled and/or rotated.
As given, this tetrahedron has:
- A side equal to 4Ö3.
- A height equal to 4Ö2.
- A circumscribed sphere of radius
3Ö2.
An alternate set of Cartesian coordinates for a smaller regular tetrahedron
(of side 2Ö2, inscribed in a sphere of radius
Ö3)
would consist of every other vertex
in a cube of side 2 (see below) centered at the origin.
This highlights some geometrical relationships and dims others:
A = [+1,+1,+1], B = [+1,-1,-1], C = [-1,+1, -1], D = [-1,-1,+1]
In such a regular tetrahedron, two vertices are seen from the center at an angle
known as the tetrahedral angle (which is very familiar to chemists)
whose cosine is -1/3 and whose value is 109.47122°...
The dihedral angle between a pair of faces is supplementary to
that angle; its cosine is 1/3 and its value is about 70.52878°
(this may be called a cubic angle, for a reason which follows).
Expressed in radians, three times this angle minus a flat angle
(p) gives the value [in steradians, sr]
of the solid angle at each corner of the tetrahedron, namely 0.55128559843...
This is about 4.387 % of the solid angle of a whole sphere
(4p).
Some astronomers prefer to use the square degree as a unit of solid angle
(a square degree equals
p2/1802 sr);
the solid angle at the corner of a regular tetrahedron is
1809.7638632... square degrees
(or 6515150 square minutes).
We may choose 3 coordinates from the set {-1,+1} in 8 different ways and these correspond
to the coordinates of the 8 vertices of a cube of side 2 centered at the origin
(and inscribed in a sphere of radius Ö3).
Seen from the center of a cube, the angular separation between corners is
either a flat angle (180° between diametrically opposed vertices),
a tetrahedral angle of cosine -1/3
(about 109.47° between the opposite corners in a face),
or a cubic angle whose cosine is 1/3 and which is
supplementary to a tetrahedral angle (about 70.53° between adjacent corners).
The solid angle at each corner of a cube is clearly p/2, namely
1/8 of a whole sphere (4p).
Similarly, there are 6 ways of choosing 3 coordinates from the set {-1,0,+1}
so that only one of them is nonzero.
These correspond to the coordinates of the 6 vertices
in a regular octahedron of side
Ö2 centered at the origin
(and inscribed in a sphere of radius 1).
From the center of a regular octahedron, two vertices are seen separated either
by a right angle (90°) or by a flat angle (180°).




-
The volume
of a regular dodecahedron is (15+7Ö5)/4
times the cube of its side.
The dihedral angle has a cosine of
-1/Ö5 and a value of about 116.565°

(2002-06-14)
Is there a systematic way to name [some] special polyhedra?
Only up to a point.
The most "generic" way is to use for polyhedra the same naming scheme as
for polygons,
by counting the number or their faces:
Thus, a tetrahedron has 4 faces, a pentahedron has 5,
a dotriacontahedron (also called triacontakaidihedron)
has 32 faces.
 However, counting just faces is not nearly enough to describe a polyhedron,
even from a topological standpoint.
In some cases, a nonstandard counting prefix is traditionally used for certain
very specific polyhedra.
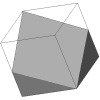
For example, the dotriacontahedron shown at right is
an Archimedean solid unambiguously known as an icosidodecahedron
(literally, a polyhedron with 20+12 faces)
because it includes 20 triangular faces and 12 pentagonal ones.
However, counting just faces is not nearly enough to describe a polyhedron,
even from a topological standpoint.
In some cases, a nonstandard counting prefix is traditionally used for certain
very specific polyhedra.
For example, the dotriacontahedron shown at right is
an Archimedean solid unambiguously known as an icosidodecahedron
(literally, a polyhedron with 20+12 faces)
because it includes 20 triangular faces and 12 pentagonal ones.
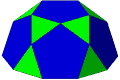 The icosidodecahedron could also be called a
pentagonal gyrobirotunda but that name would masks its much greater symmetry
compared to the related pentagonal orthobirotunda (J34).
For the same reason, a special name has been given to the cuboctahedron,
which might otherwise be called a triangular gyrobicupola.
The icosidodecahedron could also be called a
pentagonal gyrobirotunda but that name would masks its much greater symmetry
compared to the related pentagonal orthobirotunda (J34).
For the same reason, a special name has been given to the cuboctahedron,
which might otherwise be called a triangular gyrobicupola.
If the icosidodecahedron had not claimed the title for the above reason,
the name could have been given to another Archimedean solid with 32 faces,
the so-called truncated dodecahedron (which has 20 triangular faces
and 12 decagonal ones). It wasn't...
The notoriety of the icosidodecahedron has made it tempting for some (knowledgeable) people
to use the nonstandard icosidodeca prefix
(instead of dotriaconta or triacontakaidi )
to name other unrelated things
(like a 32-sided
polygon). Resist this temptation...

The general situation is similar to the
naming of chemical compounds.
Certain families can be identified and a systematic naming can be introduced
among such families.
The next article gives the most common such examples.
(2000-11-19)
What types of polyhedra are named after a polygon?
 Take a regular polygon (an hexagon, say)
and construct a polyhedron by considering an identical copy of that hexagon
in a parallel plane.
Join each vertex of the hexagon to the corresponding
vertex in its copy and you obtain what's called an hexagonal prism.
Take a regular polygon (an hexagon, say)
and construct a polyhedron by considering an identical copy of that hexagon
in a parallel plane.
Join each vertex of the hexagon to the corresponding
vertex in its copy and you obtain what's called an hexagonal prism.
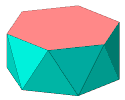 Instead, you may twist the copy slightly and join each vertex to the two
nearest vertices of the copy. What you obtain is an hexagonal antiprism.
In such families, the polyhedron is named using the adjective corresponding to the
name of the polygon
it's built on (e.g., "hexagonal").
Instead, you may twist the copy slightly and join each vertex to the two
nearest vertices of the copy. What you obtain is an hexagonal antiprism.
In such families, the polyhedron is named using the adjective corresponding to the
name of the polygon
it's built on (e.g., "hexagonal").
There are many other families besides prisms and antiprisms
for which this pattern applies.
For example, if you cut a prism with a plane containing some edge of either
base polygon (but not intersecting the other), this "half" prism is called
a wedge (it includes the base polygon and its featured edge).
Cutting an antiprism the same way, you obtain an antiwedge
(the simplest chiral polyhedron is the tetragonal antiwedge,
an hexahedron).
Alternately, if the cutting plane contains only a vertex, instead of an edge,
the polyhedron you obtain by cutting a prism is best called an hemiprism.
Some polyhedra based on an n-sided polygon
| Name | Vertices | Edges | Faces | Remarks |
| pyramid | n+1 | 2n | n+1 | One n-gon, n triangles |
| dipyramid | n+2 | 3n | 2n | 2n triangles |
deltohedron
(see note below) |
2n+2 | 4n | 2n | 2n
quadrilaterals (a cube is
a triangular deltohedron) |
| prism | 2n | 3n | n+2 | Two n-gons, n quadrilaterals
(a cube is a square prism) |
| antiprism | 2n | 4n | 2n+2 | Two n-gons, 2n triangles |
| cupola | 3n | 5n | 2n+2 | One 2n-gon, one n-gon,
n quadrilaterals, n triangles |
orthobicupola
gyrobicupola | 4n | 8n | 4n+2 | Two n-gons,
2n quadrilaterals, 2n triangles |
cupolapyramid
| 3n+1 | 7n | 4n+1 | One
n-gon,
n quadrilaterals, 3n triangles |
| rotunda | 4n | 7n | 3n+2 | One 2n-gon, one n-gon,
n pentagons, 2n triangles |
orthobirotunda
gyrobirotunda | 6n | 12n | 6n+2 | Two
n-gons,
2n pentagons, 4n triangles |
| rotundapyramid | 4n+1 | 9n | 5n+1 | One
n-gon, n pentagons,
n quadrilaterals, 3n triangles |
cupolarotunda
(ortho- / gyro-) | 5n | 10n | 5n+2 | Two
n-gons, n pentagons,
n quadrilaterals, 3n triangles |
| hemiprism | 2n-1 | 3n-1 | n+2 | Two n-gons
(sharing one vertex),
2 triangles, n-2 quadrilaterals |
| wedge | 2n-2 | 3n-3 | n+1 | Two n-gons
(sharing one edge),
2 triangles, n-3 quadrilaterals |
(left) antiwedge
(right) antiwedge | 2n-2 | 4n-6 | 2n-2 | Two n-gons,
2n-4 triangles
Only 4 vertices with 3 edges. |
-
 Note: An n-gonal deltohedron is what a regular
n-gonal dipyramid becomes if you
twist its upper pyramidal cone 1/2n of a turn with respect to the lower one:
The intersection of the two "cones" becomes a solid whose faces are quadrilaterals
[see figure at right].
Do not confuse these deltohedra with the deltahedra mentioned
next...
Note: An n-gonal deltohedron is what a regular
n-gonal dipyramid becomes if you
twist its upper pyramidal cone 1/2n of a turn with respect to the lower one:
The intersection of the two "cones" becomes a solid whose faces are quadrilaterals
[see figure at right].
Do not confuse these deltohedra with the deltahedra mentioned
next...
What are deltahedra?
[Not to be confused with the above deltohedra.]
-
Deltahedra are simply polyhedra whose faces are all equilateral triangles
(a polyhedron whose faces are triangles which are not all equilateral is
best called an irregular deltahedron).
A deltahedron [or an irregular deltahedron] has necessarily
an even number of faces (2n faces, 3n edges, and n+2 vertices).
A noteworthy fact is that there are only 8 convex deltahedra
(disallowing coplanar adjacent faces). Namely:
 |
 |
 |
 |
| 4 faces | 6 faces |
8 faces | 10 faces |
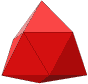
- Regular tetrahedron (4 faces).
- Triangular Dipyramid (6 faces).
- Regular octahedron or "Square Dipyramid" (8 faces).
- Pentagonal Dipyramid (10 faces).
- Snub Disphenoid (12 faces), J84.
[The Snub Disphenoid was originally called
"Siamese dodecahedron" by Freudenthal and van der Waerden,
who first described it in 1947.]
- Triaugmented Triangular Prism (14 faces), J51.
- Gyroelongated Square Dipyramid (16 faces), J17.
- Icosahedron or "Gyroelongated Pentagonal Dipyramid" (20 faces).
 |
 |
 |
 |
| 12 faces | 14 faces |
16 faces | 20 faces |
All told, the convex deltahedra include
- 3 Platonic solids (tetrahedron, octahedron and icosahedron).
- 3 dipyramids (triangular, square and pentagonal).
- 3 Johnson solids (J17, J51, and J84).
This adds up to 8, instead of 9, because the regular octahedron
happens to be counted twice
(as a Platonic solid and a square dipyramid)...
What are some [other] named polyhedra?
-
It is quite challenging to enumerate all convex polyhedra whose faces
are regular polygons. This includes first the 5 Platonic solids and
the 13 Archimedean solids (only 2 of which are chiral, the snub
cube and snub dodecahedron).
Although first discovered by Archimedes, the original classification
 was lost and only twelve Archimedean solids were known during the Renaissance.
The thirteenth (the chiral snub dodecahedron)
was added by Kepler when he reconstructed the full Archimedean classification,
in 1619.
The vertices of Archimedean solids are all equivalent and Kepler
observed that this property was also shared by two infinite families
of convex polyhedra with regular faces: the prisms and antiprisms.
The final touch was added in 1966, when Norman W. Johnson gave the full
classification of 92 other such polyhedra whose vertices are
not all equivalent.
These are now called
Johnson
solids.
Only 5 of the 92 Johnson solids are chiral
[gyroelongated triangular bicupola (J44),
gyroelongated square bicupola (J45),
gyroelongated pentagonal bicupola (J46),
gyroelongated pentagonal cupolarotunda (J47), and
gyroelongated pentagonal birotunda (J48)].
was lost and only twelve Archimedean solids were known during the Renaissance.
The thirteenth (the chiral snub dodecahedron)
was added by Kepler when he reconstructed the full Archimedean classification,
in 1619.
The vertices of Archimedean solids are all equivalent and Kepler
observed that this property was also shared by two infinite families
of convex polyhedra with regular faces: the prisms and antiprisms.
The final touch was added in 1966, when Norman W. Johnson gave the full
classification of 92 other such polyhedra whose vertices are
not all equivalent.
These are now called
Johnson
solids.
Only 5 of the 92 Johnson solids are chiral
[gyroelongated triangular bicupola (J44),
gyroelongated square bicupola (J45),
gyroelongated pentagonal bicupola (J46),
gyroelongated pentagonal cupolarotunda (J47), and
gyroelongated pentagonal birotunda (J48)].
 | |
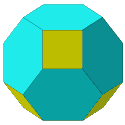
For a solid to be Archimedean, all its vertices must have the same
arrangement of faces around them, but this is not sufficient.
A counterexample is the elongated square gyrobicupola (J37),
also called pseudo-rhombicuboctahedron (pictured at left),
which is not Archimedean.
To describe these and other common polyhedra, some systematic nomenclature is useful.
 In particular, any polyhedron gives rise to many other types whose names include one
or more of the following adjectives:
In particular, any polyhedron gives rise to many other types whose names include one
or more of the following adjectives:
- Elongated: By replacing (one of) the largest m-sided polygon,
with an m-gonal prism (that polygon may not be a face of the
polyhedron, but an "internal" polygon with apparent edges).
This adds m vertices, 2m edges, and m faces.
The simplest example, shown at right, is the elongated tetrahedron (J7),
which is an heptahedron.
- Gyroelongated: By replacing (one of) the largest m-sided polygon,
with an m-gonal antiprism (that polygon is usually not a face of the
polyhedron, but an "internal" polygon with apparent edges).
This adds m vertices, 3m edges, and 2m faces.
Gyroelongation can be performed in
two different ways (often leading to different chiral versions of the same
polyhedron).
- Snub: Snubbing is an interesting chiral process which,
roughly speaking, amounts to loosening all faces of a polyhedron and rotating them
all slightly in the same direction (clockwise or counterclockwise),
creating 2 triangles for each edge and one m-sided polygon for each vertex of degree m.
A polyhedron and its dual have the same snub(s)!
If a polyhedron has k edges, its snub has 5k edges, 2k vertices and 3k+2 faces.
- Truncated: By cutting off an m-gonal pyramid at one or more
(usually all) of the vertices. This add (m-1) vertices, m edges and 1 face
for each truncated vertex.
- Augmented: By replacing one or more of the m-sided faces
with an m-gonal pyramid, cupola, or rotunda.
- etc. ...
A certain number of other terms are available to describe certain
interesting special cases:
- Cingulum (Latin: girdle; cingere to gird).
- Fastigium (Latin: apex, height).
- Sphenoid (Greek: wedge).
- etc. ...
The rest of the nomenclature used in the context of Johnson solids,
is best described in the words of Norman W. Johnson himself:
If we define a lune as a complex of two triangles attached to opposite sides of a
square, the prefix spheno- refers to a wedgelike complex formed by two adjacent lunes.
The prefix dispheno- denotes two such complexes,
while hebespheno- indicates a blunter complex of two lunes separated by a third lune.
The suffix -corona refers to a crownlike complex of eight triangles,
and -megacorona, to a larger such complex of 12 triangles.
The suffix -cingulum indicates a belt of 12 triangles.
There is an important relation among different types of polyhedra which is of primary
importance when enumerating them.
Each polyhedron has a dual which is obtained
essentially by interchanging the role of vertices and faces. A polyhedron and its dual
have the same number of edges but each edge is seen in the dual as connecting two
faces instead of two vertices. Duality is a topological transformation which has
only an indirect geometrical equivalent. The duals of Archimedean polyhedra are
called Catalan solids.

The names of chiral polyhedra are starred (*).
Platonic
Solids |
F | E |
V | Duals |
|---|
| Tetrahedron | 4 | 6 | 4 | Tetrahedron |
|---|
| Cube | 6 | 12 | 8 | Octahedron |
|---|
| Octahedron | 8 | 12 | 6 | Cube |
|---|
| Dodecahedron | 12 | 30 | 20 |
Icosahedron |
|---|
| Icosahedron | 20 | 30 | 12 |
Dodecahedron |
|---|
Archimedean
Solids |
F | E | V | Duals
(Catalan Solids) |
|---|
| Truncated Tetrahedron | 8 | 18 | 12 |
Triakis Tetrahedron |
|---|
| Cuboctahedron | 14 | 24 | 12 |
Rhombic Dodecahedron |
|---|
| Truncated Cube | 14 | 36 | 24 |
Triakis Octahedron |
|---|
| Truncated Octahedron | 14 | 36 | 24 |
Tetrakis Cube |
|---|
| Rhombicuboctahedron | 26 | 48 | 24 |
Deltoidal Icositetrahedron |
|---|
| Great Rhombicuboctahedron | 26 | 72 | 48 |
Disdyakis Dodecahedron |
|---|
| Icosidodecahedron | 32 | 60 | 30 |
Rhombic Triacontahedron |
|---|
| Truncated Icosahedron | 32 | 90 | 60 |
Pentakis Dodecahedron |
|---|
| Truncated Dodecahedron | 32 | 90 | 60 |
Triakis Icosahedron |
|---|
| Snub Cube* | 38 | 60 | 24 |
Pentagonal Icositetrahedron* |
|---|
| Rhombicosidodecahedron | 62 | 120 | 60 |
Deltoidal Hexacontahedron |
|---|
| Great Rhombicosidodecahedron | 62 | 180 | 120 |
Disdyakis Triacontahedron |
|---|
| Snub Dodecahedron* | 92 | 150 |
60 | Pentagonal Hexacontahedron* |
|---|
-
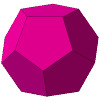
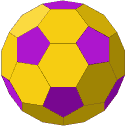 The truncated icosahedron (the shape of a traditional soccer ball)
is now more commonly known as a buckyball ever since it was found to be
the structure of a wonderful new molecule,
now called fullerene (C60)
in honor of the famous American architect R. Buckminster ("Bucky") Fuller (1895-1983),
who created and advocated
geodesic domes
in the late 1940s.
The truncated icosahedron (the shape of a traditional soccer ball)
is now more commonly known as a buckyball ever since it was found to be
the structure of a wonderful new molecule,
now called fullerene (C60)
in honor of the famous American architect R. Buckminster ("Bucky") Fuller (1895-1983),
who created and advocated
geodesic domes
in the late 1940s.
The buckyball is one of 4
Archimedean
solids without triangular faces.
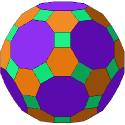
 The other three are the truncated octahedron (at left),
the great rhombicosidodecahedron (at right)
and the great rhombicuboctahedron.
The other three are the truncated octahedron (at left),
the great rhombicosidodecahedron (at right)
and the great rhombicuboctahedron.

The 4 Archimedean polyhedra illustrated
so far are simplicial
(i.e., only 3 edges meet at each vertex).
There are 3 others such simplicial polyhedra, illustrated next,
which happen to be obtained
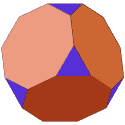
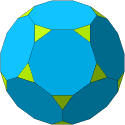
(like the buckyball and truncated octahedron above)
by truncating a Platonic solid.
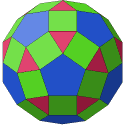



Finally, 5 edges meet at every vertex of the two chiral
Archimedean polyhedra:

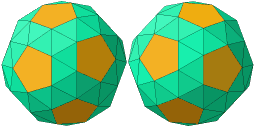
The full classification of these 13 solids is believed to have been discovered by
Archimedes of Syracuse (c.287-212 BC), but the work was lost and the thirteenth
of them (the Snub Dodecahedron, whose two chiralities are pictured above right)
was apparently forgotten until Kepler (1571-1630)
reconstructed the whole set, in 1619.
-
How do polyhedra generalize to dimension 4 or more?
-
The equivalent of a polyhedron in dimension 4 is called a polychoron
(plural polychora).
Polychora are discussed extensively on beautifully illustrated pages proposed by
George Olshevsky and
Jonathan Bowers.
Although the introduction of the term polychoron is fairly recent,
it seems now generally accepted, as there's no serious competition
(the etymology of "polyhedroid" is poor and misleading).
The term was coined in the 1990's by
George Olshevsky, whose
earlier proposal of "polychorema" (plural: "polychoremata") was unsuccessful.
Olshevsky's new proposal had the early support of Norman W. Johnson,
after whom the 92 "convex regular-faced solids" are named (Johnson solids).
A polychoron is bounded by 3-dimensional faces, called cells.
The four-dimensional equivalent of the Euler-Descartes formula is a topological relation
which relates the number of vertices (V), edges (E), faces (F), and cells (C)
in any polychoron enclosing a portion of hyperspace homeomorphic to
a 4D open ball (provided edges, faces and cells
are homeomorphic, respectively, to 1D, 2D and 3D open balls):
V - E + F - C = 0
In an unspecified number of dimensions, the counterpart of a 2D polygon,
a 3D polyhedron, or a 4D polychoron is called a polytope.
The boundary of an n-dimensional polytope consists of hyperfaces
which are (n-1)-dimensional polytopes,
joining at hyperedges, which are (n-2)-dimensional polytopes.
(All the hyperfaces of an hyperface are thus hyperedges.)
This vocabulary is consistent with the well-established term
hyperplane to designate a vector space of codimension 1
(in a hyperspace with a finite number n of dimensions, a hyperplane is
therefore a linear space of dimension n-1).
We also suggest the term hyperline for a linear space of codimension 2
(and, lastly, hyperpoint to designate a space of codimension 3).
To denote the p-dimensional polytopes within a polytope of dimension n, the following
terms may be used: vertex (p=0; plural "vertices"), edge (p=1), face (p=2),
cell or triface (p=3), tetraface (p=4), pentaface (p=5), hexaface (p=6),
... hypervertex (p=n-3),
hyperedge (p=n-2), hyperface (p=n-1), hypercell (p=n).
To establish and/or memorize the n-dimensional equivalent of the Euler-Descartes
formula for "ordinary" polytopes in n dimensions, it's probably best to
characterize each such polytope by the open region it encloses (boundary excluded),
except in dimension zero (the 0-polytope is a single point).
For the formula to apply, each such region should be homeomorphic [i.e., topologically
equivalent] to the entire Euclidean space of the same dimension, or equivalently to
an open ball of that dimension.
An edge is an open segment, a face is an open disk, a cell is an open ball, etc.
[for example, the ring between two concentric circles is not allowed as a face,
and the inside of a torus is disallowed as a cell].
Then we notice that a number can be assigned to any polytope (and a number of other
things) called its Euler characteristic (c),
which is additive for disjoint sets,
equal to 1 for a point and invariant in a topological homeomorphism
(so that topologically equivalent things have the same c).
For our purposes, this may be considered an axiomatic definition of
c.
It may be used to establish (by induction)
that the c of n-dimensional
Euclidean space is (-1)n,
which is therefore equal to the c of our
"ordinary" open polytopes
(HINT: A hyperplane separates hyperspace into
three parts; itself and 2 parts homeomorphic to the whole hyperspace).
The c of all "ordinary" closed polytopes in n dimensions
is the c of a closed n-dimensional ball and it may
be obtained by inspecting the components of the boundary of any easy n-dimensional
polytope like the hypercube or the simplex polytope discussed below.
It turns out to be equal to 1 in any dimension n.
If the hypercell itself (the polytope's interior) is excluded from the count,
as it is in the traditional 3-dimensional Euler-Descartes formula, the RHS of the formula will
therefore be 2 in an odd number of dimensions and zero in an even number of dimensions.
For example, in 7 dimensions, if we denote by T the number of tetrafaces, by P the number
of pentafaces (hyperedges), and by H the number of hexafaces (hyperfaces), we have:
V - E + F - C + T - P + H = 2
We may focus on the n-dimensional equivalent of the Platonic solids, namely
the regular convex polytopes,
whose hyperfaces are regular convex polytopes
of a lower dimension, given the fact that the concept reduces to
that of a regular polygon [equiangular and equilateral] in dimension 2.
In dimension 3, this gives the 5 regular polyhedra.
In dimension 4, we have 6 regular polychora.
In dimension 5 or more, only 3 regular polytopes exists which belong to one of the following
three universal families (also present in spaces of lower dimensions):
| Family | n-Polytope | dim. |
V
0 | E
1 | F
2 | C
3 | T
4 |
p-Faces
p |
|---|
| Simplex |
| n |
C(n+1,p+1) |
| Point |
0 | 1 |
| Segment |
1 | 2 | 1 |
| Triangle |
2 | 3 | 3 | 1 |
| Tetrahedron |
3 | 4 | 6 | 4 | 1 |
| Pentachoron |
4 | 5 | 10 | 10 | 5 | 1 |
Cross
Polytope |
| n |
C(n,p+1) 2p+1 |
| Point |
0 | 1 |
| Segment |
1 | 2 | 1 |
| Square |
2 | 4 | 4 | 1 |
| Octahedron |
3 | 6 | 12 | 8 | 1 |
| Hexadecachoron |
4 | 8 | 24 | 32 | 16 | 1 |
| Hypercube |
| n |
C(n,p) 2n-p |
| Point |
0 | 1 |
| Segment |
1 | 2 | 1 |
| Square |
2 | 4 | 4 | 1 |
| Cube |
3 | 8 | 12 | 6 | 1 |
| Tesseract |
4 | 16 | 32 | 24 | 8 | 1 |
The regular simplex polytope is obtained by considering n+1 vertices in dimension n,
so that each one is at the same distance from any other
(its hyperfaces are simplex polytopes of a lower dimension).
Choosing as vertices all points whose Cartesian coordinates are from the
set {-1,+1}, we obtain an n-dimensional hypercube (of side 2).
The hyperfaces of an hypercube are hypercubes of a lower dimension.
The dual of the above hypercube is the regular cross polytope whose
vertices have a single nonzero coordinate, taken from the set {-1,+1}.
The 5D interactive hypercube at right is from
Kurt Brauchli (details
here).
Click and drag with the mouse to turn the cube aound the chosen axes (H and V)
indicated in the menu bar.
This 5D cube projects like a 3D cube if you rotate
only around axes 0, 1 or 2.
The fourth and fifth dimensions appear with axes 3 and 4.
With the bottom cursor, you may choose a distant (left) or close-up perspective (right).
|
|
EnolaStraight
(2002-05-07)
What's the radius of the circle touching 3 touching unit circles?
What's the radius of the sphere touching 4 touching unit spheres?
[In this (edited) question, "touching" means "externally tangent (to)".]
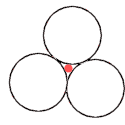
The generalization of this question to any number of dimensions is a classic demonstration
that whatever geometrical intuition we may have developed in two or three
dimensions may not be trusted in a space of more dimensions.
The two-dimensional case [pictured at right] shows 3 congruent circles, centered on the
vertices of an equilateral triangle, touching each other and a much smaller circle
[pictured as a red disk] whose radius has to be determined.
Based on this 2-D case [and, to a lesser extent, on the 3-D case] it would seem that
such an inner ball [disk, sphere, or n-dimensional hypersphere] would always be
small enough to fit inside the simplex [equilateral triangle, regular tetrahedron,
n-dimensional regular simplex] formed by the centers of the congruent balls.
This happens to be true for a dimension equal to 4 or less, but fails for a dimension of
5 or more. In a very large number of dimension,
the (linear) size of the inner ball is about 41% the size of the outer ones.
More precisely,
Ö2-1 = 0.41421356...
is the limit of that ratio when the number of dimensions tends to infinity.
Read on...
Consider the center O of the n-dimensional simplex
formed by the n+1 centers of the congruent balls [each of radius 1].
The critical quantity is the distance D(n) from the center O to any vertex;
the radius of the inner ball is simply D(n)-1.
Well, because O is the center of gravity of n+1 vertices, it is on the line that goes from
a vertex to the center of gravity of the n others. It divides that line in a 1 to n ratio.
The length of that line is therefore (1+1/n)D(n) and it is also one side of a
right triangle whose other side is of length D(n-1) and whose hypotenuse is of
length 2 (it's the side of the simplex, the distance between the centers of two balls).
In other words, D(n) is given recursively by the relations:
D(1) = 1 and
D(n) = Ö[4-D(n-1)2] / (1+1/n)
This recursion can be used to prove by induction the following simple formula:
D(n) = Ö[ 2n / (n+1) ]
The simplicity of this result is a hint that there might be a more direct way to obtain it.
D(2) = 2/Ö3 says that the radius of the
inner circle in the above figure is
2/Ö3-1
[about 15.47 %] of the radius of any outer circle.
Similarly, the corresponding ratio for spheres is
½Ö6-1
[about 22.4745 %].
The limit of D(n) is Ö2:
In a space with a very large number of dimensions,
the ratio of the radius of the inner hypersphere to the radius of any outer hyperspheres is
thus slightly less than
Ö2-1
[about 41.42 %].
In dimension n, the distance from the center O to any of the hyperplanes
(of dimension n-1)
which carry the "faces" of the simplex is D(n)/n.
Therefore, if the radius D(n)-1 is greater than is D(n)/n.,
the inner hypersphere bulges outside of the n-dimensional regular simplex formed
by the centers of the outer hyperspheres.
This happens as soon as n2-5n+2 > 0,
which is the case when n is at least equal to 5.
This higher-dimensional configuration is contrary to the intuition we would form
by looking only at the two-dimensional and/or three-dimensional cases...
 Dr.
Murali V.R. (2004-02-25; e-mail) Dr.
Murali V.R. (2004-02-25; e-mail)
What is the volume of a regular antiprism?
A regular antiprism is a polyhedron whose faces are
two parallel n-gonal bases [regular polygons with n sides]
and 2n equilateral triangles called lateral faces.
Look at the outline of such a solid from above, and what you see
is a regular polygon with 2n sides (every other vertex is on the top base,
and every other one is on the bottom).
The angle at each vertex of this outline is thus
q = p-p/n.
Now, each lateral face is seen as an isosceles triangle having an angle
q at the top
and featuring a base observed at its real size a
(as the direction of observation is perpendicular to it).
The height of such an isoceles triangle is thus:

½ a cotan (q/2)
=
½ a tan (p/2n)
This quantity is also equal to the length of a side of a right triangle
whose hypotenuse is the true height
of a lateral face (namely ½ aÖ3)
and whose other side is the height h of the antiprism
(namely, the distance between its bases).
This gives the height h of the antiprism in terms of
the length a of its edges:
|
 |
| h = ½ a |
Ö |
3 - tan2(p/2n) |
Consider the circumscribed prism of height h
whose base is the 2n-gonal outline.
Each side of this outline is equal to
½ a / cos(p/2n).
Its surface area is therefore:
(n a2/4) /
sin(p/n) and the volume
of the prism is h times that.
The antiprism is obtained from this prism by removing
2n triangular pyramids of height h
whose bases are all congruent to the above isosceles triangle,
for a combined base area of
(n a2/2) tan(p/2n)
and a total volume h/3 times that.
The volume V of the antiprism is the difference between these two volumes:
|
 |
| V = (n a3 / 24)
[ 3 / sin(p/n)
- 2 tan (p/2n) ] |
Ö |
3 - tan2(p/2n) |
This can be rewritten in a much more palatable form, using
t = tan (p/2n) :
V = n a3
( 3 - t 2 ) 3/2
/ 48t
|
 |
|
| h = ½ a |
Ö |
3 - tan2(p/2n) |
V = n h 3
/ 6 tan(p/2n) |
|
 Two noteworthy special cases (for a = 1):
Two noteworthy special cases (for a = 1):
- V = 1 / Ö72 when n=2. A regular tetrahedron!
[A degenerate but valid case.]
- V = ½ Ö3 when n=3.
A regular octahedron...
|



 (like the buckyball and truncated octahedron above)
by truncating a Platonic solid.
(like the buckyball and truncated octahedron above)
by truncating a Platonic solid.


 (Jerry of Nashville, TN.
(Jerry of Nashville, TN.


 The tetragonal antiwedge is the least symmetrical of all hexahedra;
its only possible symmetry is a 180° rotation.
This skewed hexahedron has
the same number of edges and vertices as the pentagonal pyramid.
Its faces consist of 4 triangles and 2 quadrilaterals.
Such a solid is obtained from two quadrilaterals
that share an edge [the hinge]
but do not form a triangular prism.
After adding two edges to complete the two triangles whose sides are adjacent to
the hinge, we are left with a nonplanar quadrilateral
and must choose one of its 2 diagonals as the last edge of the polyhedron.
Only one choice gives a convex polyhedron.
The tetragonal antiwedge is the least symmetrical of all hexahedra;
its only possible symmetry is a 180° rotation.
This skewed hexahedron has
the same number of edges and vertices as the pentagonal pyramid.
Its faces consist of 4 triangles and 2 quadrilaterals.
Such a solid is obtained from two quadrilaterals
that share an edge [the hinge]
but do not form a triangular prism.
After adding two edges to complete the two triangles whose sides are adjacent to
the hinge, we are left with a nonplanar quadrilateral
and must choose one of its 2 diagonals as the last edge of the polyhedron.
Only one choice gives a convex polyhedron.

 The other types of hexahedra are more symmetrical and simpler to visualize.
One of them may be constructed by cutting off
one of the 4 base corners of a square pyramid to create a new triangular face.
This hexahedron has 7 vertices and 11 edges.
The other types of hexahedra are more symmetrical and simpler to visualize.
One of them may be constructed by cutting off
one of the 4 base corners of a square pyramid to create a new triangular face.
This hexahedron has 7 vertices and 11 edges.
 Its faces include 3 triangles, 2 quadrilaterals and 1 pentagon.
It could also be obtained by cutting an elongated square pyramid
(the technical name for an obelisk)
along a bisecting plane through the apex of the pyramid and the
diagonal of the base prism, as pictured at right.
For lack of a better term, we may therefore call this hexahedron an
hemiobelisk.
Its faces include 3 triangles, 2 quadrilaterals and 1 pentagon.
It could also be obtained by cutting an elongated square pyramid
(the technical name for an obelisk)
along a bisecting plane through the apex of the pyramid and the
diagonal of the base prism, as pictured at right.
For lack of a better term, we may therefore call this hexahedron an
hemiobelisk.
 Also with 7 vertices and 11 edges, there's a solid which we may call
a hemicube (or square hemiprism), obtained
by cutting a cube in half using a plane going through two opposite corners and
the midpoints of two edges. Its 6 faces include 2 triangles and
4 quadrilaterals.
Also with 7 vertices and 11 edges, there's a solid which we may call
a hemicube (or square hemiprism), obtained
by cutting a cube in half using a plane going through two opposite corners and
the midpoints of two edges. Its 6 faces include 2 triangles and
4 quadrilaterals.

 to the distance from a side to an adjacent vertex, namely
to the distance from a side to an adjacent vertex, namely








 However, counting just faces is not nearly enough to describe a polyhedron,
even from a topological standpoint.
In some cases, a nonstandard counting prefix is traditionally used for certain
very specific polyhedra.
For example, the dotriacontahedron shown at right is
an Archimedean solid unambiguously known as an icosidodecahedron
(literally, a polyhedron with 20+12 faces)
because it includes 20 triangular faces and 12 pentagonal ones.
However, counting just faces is not nearly enough to describe a polyhedron,
even from a topological standpoint.
In some cases, a nonstandard counting prefix is traditionally used for certain
very specific polyhedra.
For example, the dotriacontahedron shown at right is
an Archimedean solid unambiguously known as an icosidodecahedron
(literally, a polyhedron with 20+12 faces)
because it includes 20 triangular faces and 12 pentagonal ones.
 The icosidodecahedron could also be called a
pentagonal gyrobirotunda but that name would masks its much greater symmetry
compared to the related pentagonal orthobirotunda (J34).
For the same reason, a special name has been given to the cuboctahedron,
which might otherwise be called a triangular gyrobicupola.
The icosidodecahedron could also be called a
pentagonal gyrobirotunda but that name would masks its much greater symmetry
compared to the related pentagonal orthobirotunda (J34).
For the same reason, a special name has been given to the cuboctahedron,
which might otherwise be called a triangular gyrobicupola.
 Take a regular polygon (an hexagon, say)
and construct a polyhedron by considering an identical copy of that hexagon
in a parallel plane.
Join each vertex of the hexagon to the corresponding
vertex in its copy and you obtain what's called an hexagonal prism.
Take a regular polygon (an hexagon, say)
and construct a polyhedron by considering an identical copy of that hexagon
in a parallel plane.
Join each vertex of the hexagon to the corresponding
vertex in its copy and you obtain what's called an hexagonal prism.
 Instead, you may twist the copy slightly and join each vertex to the two
nearest vertices of the copy. What you obtain is an hexagonal antiprism.
In such families, the polyhedron is named using the adjective corresponding to the
Instead, you may twist the copy slightly and join each vertex to the two
nearest vertices of the copy. What you obtain is an hexagonal antiprism.
In such families, the polyhedron is named using the adjective corresponding to the
 Note: An n-gonal deltohedron is what a regular
Note: An n-gonal deltohedron is what a regular




 In particular, any polyhedron gives rise to many other types whose names include one
or more of the following adjectives:
In particular, any polyhedron gives rise to many other types whose names include one
or more of the following adjectives:
 The truncated icosahedron (the shape of a traditional soccer ball)
is now more commonly known as a buckyball ever since it was found to be
the structure of a wonderful new molecule,
now called fullerene (C60)
in honor of the famous American architect R. Buckminster ("Bucky") Fuller (1895-1983),
who created and advocated
The truncated icosahedron (the shape of a traditional soccer ball)
is now more commonly known as a buckyball ever since it was found to be
the structure of a wonderful new molecule,
now called fullerene (C60)
in honor of the famous American architect R. Buckminster ("Bucky") Fuller (1895-1983),
who created and advocated
 The other three are the truncated octahedron (at left),
the great rhombicosidodecahedron (at right)
and the great rhombicuboctahedron.
The other three are the truncated octahedron (at left),
the great rhombicosidodecahedron (at right)
and the great rhombicuboctahedron.



