The speed of sound in a gas mixture depends on the composition of the mixture, via the equation v=SQRT(B/D), where D is the density of the mixture and B is called the bulk modulus. This has a small but noticeable effect on the pitch of a woodwind instrument, which we can estimate via differentials.
Let p be the proportion (partial pressure) of CO2 in the air exhaled from the player's lungs into the instrument. The value of p is 0 immediately after "taking a breath" and can increase to 0.085 during a very long musical phrase (i.e. 8.5% of the exhaled air is CO2).
Both D and B (and hence v and also pitch) depend on p. It can be shown that D(p)=D(0)(1+0.42p) and B(p)=B(0)(1-0.10p). EXERCISE: Use differentials to show that v(p)=v(0)(1-0.26p), approximately. Thus calculate the percentage decrease in v as p increases from 0 to 0.085 (8.5%).
It can further be shown, though it will take us until March to learn the math, that such a decrease in sound speed creates a flattening of pitch of about 4.5p semitones, which the player has to compensate for by air pressure and other means. For more details, if you don't mind that some of the math or physics gets a bit hairy, see the following articles on the web:
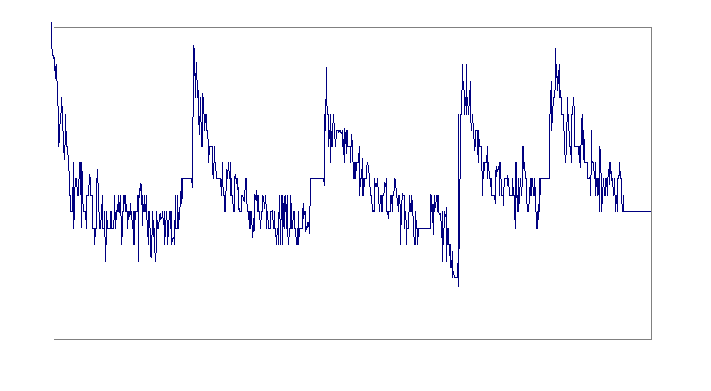
Experimentally measured pitch effect on a bassoon (stolen from [Fuks]):
