Area of a polygon
I
was recently asked to find an algorithm to calculate the area of a
polygon. I was given the co-ordinates of the vertices in order and I
was told to assume that the polygon did not intersect itself. I was
able to come up with some solution which involved triangulating the
polygon, however that solution was no good as it would not work with
certain types of polygons. How would you come up with this algorithm?
Remember that your solution has to also work for polygons that are
wierdly shaped. You cannot assume that the polygon is convex. Here are
some examples….

Suppose the vertices of the polygon are given by 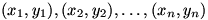 where the nth set of co-ordinates is equal to the first, then the area of the polygon is given by the nice formula
where the nth set of co-ordinates is equal to the first, then the area of the polygon is given by the nice formula
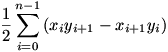 .
.A really nice solution to this problem is using Green’s Theorem. This theorem equates a line integral around the boundary of a simple region to a double integral. The theorem states that if C is a piecewise smooth, simple, closed curve in a plane and it encloses a region D, then
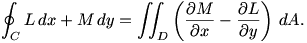
If we can choose L and M such that 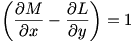 , then the double integral on the right hand side in Green’s Theorem will just calculate the area of the region D. One option is to take
, then the double integral on the right hand side in Green’s Theorem will just calculate the area of the region D. One option is to take 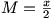 and
and  .
.
If D is the polygon and C is the boundary, all we need to do to calculate the area of D is to calculate the line integral on the left hand side in Green’s Theorem. Consider the path integral from 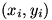 to
to 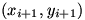 of
of 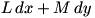 . The path is parametrized by a function
. The path is parametrized by a function 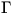 from
from ![[0,1] [0,1]](planimeter_sameer_files/ccfcd347d0bf65dc77afe01a3306a96b.gif) to the line joining
to the line joining 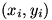 to
to 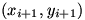 , and is given by
, and is given by

So the path integral becomes
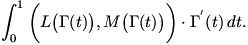

This simplifies to
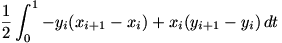
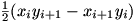 . So if we take the line integral over the closed path C,
we get the formula for the area which is written above. Of course, if
we get a negative number for the area, this would mean that C was not positively oriented and we should take the absolute value to get the area.
. So if we take the line integral over the closed path C,
we get the formula for the area which is written above. Of course, if
we get a negative number for the area, this would mean that C was not positively oriented and we should take the absolute value to get the area.

October 30th, 2005 at 1:00 pm
Nice article.
It might be worth mentioning that there is a relatively easy way to check if the points are ordered in a counter-clockwise way even if they were not given as such. It’s described for instance in “Introduction to Algorithms”.
It is probably not too hard to check whether the polygon is simple either, though off the top of my head I don’t see if one can do it in linear time.
The formula kind of makes sense I guess. Here’s another way to obtain it:
If you imagine that the polygon is star-shaped, then there is a center O such that the segments joining each vertex with O are fully contained in the polygon, Then, if we imagine that the coordinate axes are centered at O, then we can join the O to each vertex, and compute the areas of the resulting triangles. The area of the triangle formed by points i and i+1 would be half the length of the cross-products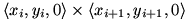 , which is exactly what your formula says.
, which is exactly what your formula says.
In fact, one can do an induction to get it in the general case (once the answer is known of course, or guessed by the reasoning above). Notice that if are consecutive points, and they are such that the triangle they form is contained in the polygon, then we can join
are consecutive points, and they are such that the triangle they form is contained in the polygon, then we can join 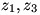 with a straight line, and break the polygon into two polygons, one the
triangle, and the other the polygon arising after omitting
with a straight line, and break the polygon into two polygons, one the
triangle, and the other the polygon arising after omitting  .
Notice that the above formulas applied to the two polygons and then
added give us exactly the formula for the big polygon, since they will
have the term
.
Notice that the above formulas applied to the two polygons and then
added give us exactly the formula for the big polygon, since they will
have the term 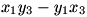 appearing with opposite signs, and everything else as it should be.
Hence by induction that would tell us that the formula does indeed
express the area of the polygon, once we know it for triangles.
appearing with opposite signs, and everything else as it should be.
Hence by induction that would tell us that the formula does indeed
express the area of the polygon, once we know it for triangles.
All that remains now would be to show that in any polygon there should be at least three consecutive points such that the triangle they form is contained in the polygon. It is clear from the pictures, but I’m not yet 100% sure how to prove it, though I feel it should follow from the methods that tell us about the correct orientation of the vertices.
November 7th, 2005 at 6:19 pm
Good work, Haris ! GI and I have just a couple of small observations to make, on this:
! GI and I have just a couple of small observations to make, on this:
Firstly, the assumption you quote in your last paragraph is equivalent to the existence of a triangulation for any polygon, so I think one can safely assume it.
Next, instead of “star-shaped”, choose and fix ANY point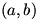 in the plane, which we use to join to each vertex. If it helps, you
could even put the point in “general position”, so that no two vertices
are in the same line with this point. (It’s not needed for the proof.)
in the plane, which we use to join to each vertex. If it helps, you
could even put the point in “general position”, so that no two vertices
are in the same line with this point. (It’s not needed for the proof.)
How does this not matter in the guessing of the formula? As you say, guess the area of a triangle, formed by joining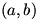 to
to 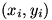 - and now sum this cyclically over i. The point is that the area is just the determinant with rows
- and now sum this cyclically over i. The point is that the area is just the determinant with rows 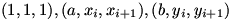 ,
and if you look at the coefficients of a,b, then they cancel out in the
cyclic sum! So you are left with exactly the sum of the cross-term
differences.
,
and if you look at the coefficients of a,b, then they cancel out in the
cyclic sum! So you are left with exactly the sum of the cross-term
differences.
And finally, given that you are assuming the existence of a triangulation, you do not need to say “by induction” in proving it, once you know the guess. The moment you sum up “correctly” over any such triangulation,
(i) the areas outside the polygon cancel each other off, since they do so for every sub-summation over a triangle contained in the triangulation, and
(ii) once you sum up correctly, the triangles formed by “inside edges” also cancel each other off, being counted once each in opposite directions.
So you are left with exactly what you need - and it equals the sum of the cross-term differences.